考虑土体非线性的内支撑支护体系优化设计
2012-09-25张四国
张四国
(天津市市政工程设计研究院,天津市 300051)
0 前言
随着城市建设的发展,基坑工程不断涌现。内支撑支护体系在深基坑工程中有着广泛的应用。支护结构虽多为临时结构,但其在工程造价中往往占有相当的比重。以市政工程中常见的地道深基坑为例,支护结构一般可以占到工程造价的1/3甚至更多。因此,在确保工程安全的前提下,进行支护结构的优化设计具有十分重要的经济意义。本文以一种常见的内支撑支护体系——单排桩+钢管撑为研究对象,进行支护结构的优化设计研究。
1 设计理论与方法
目前,关于基坑支护设计的理论与计算方法主要有极限平衡法、土抗力法和有限元法。其中,土抗力法中的弹性支点法(全称弹性地基杆系有限元单元法)[1]应用最为广泛,综合效果最好。
1.1 弹性支点法
弹性支点法采用土的线弹性本构关系。其计算原理是建立支护结构的杆系有限元模型,按朗金土压力理论计算主动土压力,即式(1),并将其作用于基坑外侧开挖面以上的支护结构;基坑开挖面以下的土体用土弹簧模拟(见图1),土弹簧的刚度系数k采用“m”法计算得到。
k=C×a×b (1)
C=m×z (2)式(1)、(2)中:C——地基土的水平基床系数,kN/m3;
m——地基土的水平基床系数的比例系数,kN/m3;z——计算深度,m;
a、b——与单元有关的参数。
1.2 考虑非线性作用的弹性支点法
上述1.1节中,开挖面以下各土层的土压力与支护结构的水平位移成线性关系,即m值为一常数,这与事实不符[2]。为更接近实际情况,考虑土的非线性作用,引入与支护结构水平位移相关的m值表述式[3]:
m=1/[1/m0+zu/(e-e0)](3)式(3)中:m0——地基土的初始水平基床系数的比例系数,kN/m4;u——支护结构的水平位移(m),主动位
移为负,被动位移为正;
z——自地面或开挖面以下计算点的深度,m;e——极限状态土压力(kPa),u<0时为主动土压力 ea,u>0 时为被动土压力 ep;e0——静止土压力,kPa。
2 优化设计的数学模型
优化设计是与常规设计相对而言的,常规设计提供“可行的”方案,优化设计则是在诸多“可行的”方案中选择出一种“最优的”方案。进行结构的优化设计首先要建立优化设计的数学模型。具体到单排桩+钢管内支撑支护体系,其优化设计的数学模型需确定如下内容:
(1)参数及变量
给定一部分参数来描述结构的特性,这些参数在优化设计过程中作为常量考虑。本文给定的参数有:各土层参数、桩径、桩距、基坑开挖深度、桩长等;变量有:支撑中心距桩顶的垂直距离h、加撑前的开挖深度d。
(2)目标函数
目标函数是评价设计方案优劣的标准。本文拟定的目标函数为:桩身水平位移最大值u、桩身弯矩最大值M。
(3)约束条件
约束条件是设计中须满足的各限制条件。对支护结构一般应满足:强度、刚度和稳定要求。
3 优化设计分析
以天津市某地道工程中的一段基坑为例,按本文前述的相关理论与方法开展支护结构的优化设计分析。
工程所处主要地层情况如下:
(1)填土层。重度18 kN/m3,厚度3.0 m,粘聚力c=5 kPa,内摩擦角 φ=8°。
(2)粉土层。重度19 kN/m3,厚度5m,粘聚力c=10 kPa,内摩擦角 φ=20°。
(3)粘土层。重度19 kN/m3,厚度15 m,粘聚力c=16 kPa,内摩擦角 φ=17°。
地下水埋深0.5 m。
基坑开挖深度do=7 m,其支护结构为单排桩+钢管内支撑。桩径为0.8 m,桩中心距为1.0 m,竖向设一道钢管撑,钢管直径为600 mm,水平中心间距为4.0 m。本文按1.2节中考虑土体非线性作用的弹性支点法建立如图1所示计算模型。支护位置的边界条件由式(3)确定。
T=kt(y-y0)+T0(4)式(4)中:kt——支点水平刚度系数,由支撑的弹性模量、规格及支撑间距确定,按文献[1]附录C中计算,kN/m;
y——支点水平位移值,m;
y0——支点设置前的水平位移值,m;T0——支点预加力,kN。
3.1 对h的优化
针对单排桩+钢管内支撑支护体系支撑点位置的优化,已有学者[4-5]进行了一定的工作,但均没有考虑土体非线性的影响,且其结论停留于单一特定结构,没有给出普遍适用的结果。
在前文第2节的模型中,取h∈[0.4,2.0],单位m,步长为0.2 m,计算得到u、M值。为使结果更具普适性,令f=h/d0,即引入参数使其等于支撑点深度/开挖深度。参数f与u、M的关系如图2所示。
由图2可看出当f=0.2时,即支撑点位置等于开挖深度的1/5时,支护结构桩身最大水平位移u有最小值;桩身最大弯矩M在f∈[0.05,0.3]范围内单调递减。建议对竖向设一道撑的单排桩+钢管内支撑支护体系,支撑点可置于开挖深度的1/5附近。
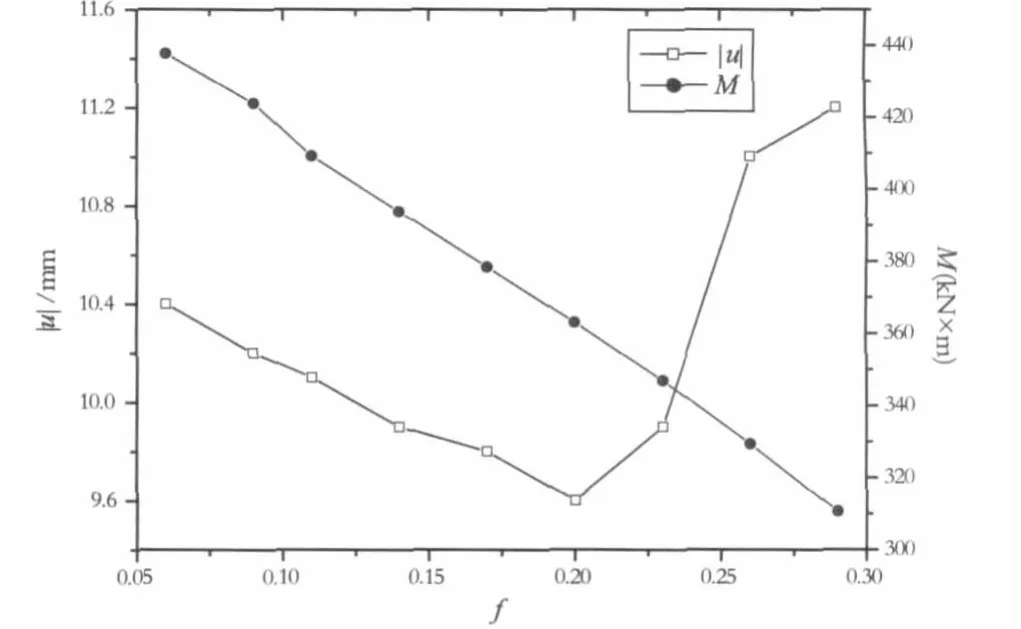
图2 f与u、M关系图
3.2 对d的优化
当 h=0.4时,取 d∈[0.4,3.6],单位 m,步长为0.2 m。同本文3.1节引入参数n,使得n=d/d0。参数n与u、M的关系如图3、图4所示。
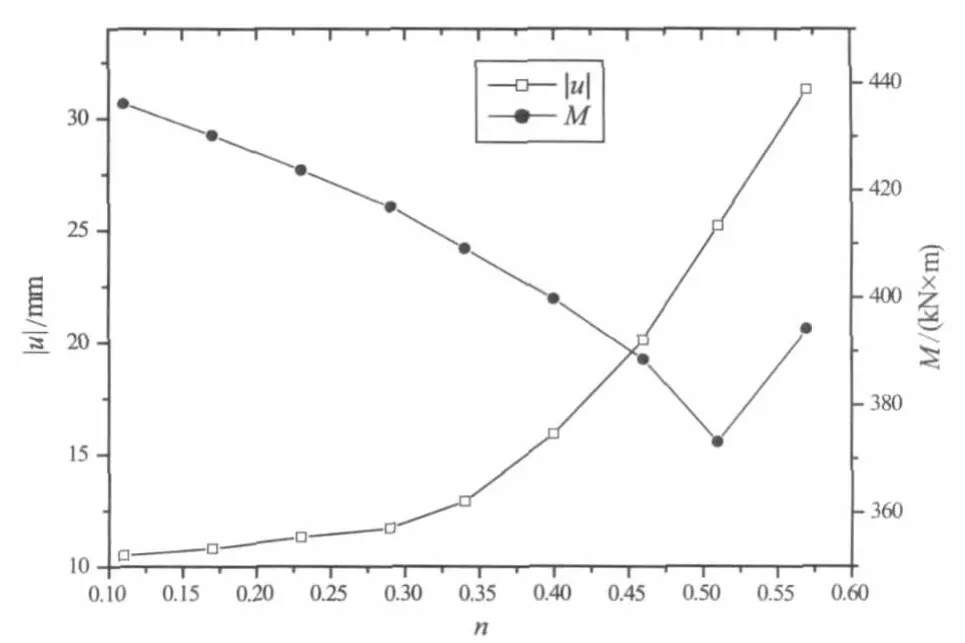
图3 n与u、M关系图(h=0.4 m)
由图3、图4可看出对于不同的h,当n=0.5左右时,支护结构桩身最大弯矩M有最小值;桩身最大水平位移u在n∈[0.1,0.6]范围内单调递增。建议对竖向设一道撑的单排桩+钢管内支撑支护体系,加撑前可适当增加超挖深度,以充分利用支护结构抗反向弯矩的能力。
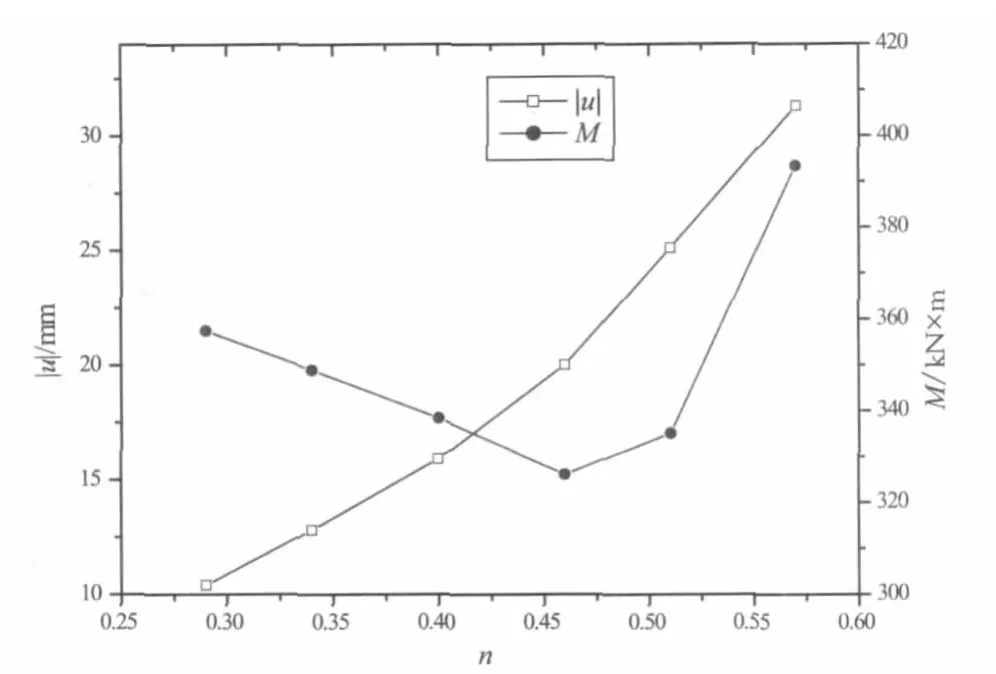
图4 n与u、M关系图(h=1.4 m)
4 结语
文章针对两个因素:支撑点位置、加撑前的开挖深度,对竖向设一道撑的单排桩+钢管内支撑支护体系开展优化设计研究。文章考虑土体的非线性作用,更符合实际,通过引入参数f、n得到了一些具备普适性的建议。需要指出的是,文章只针对竖向设一道撑的支护结构进行分析,对设两道撑或多道撑的结构还需进一步深化研究。实际工程中要考虑的因素很多,应充分结合客观情况采用切实可行的措施,在保证安全的前提下达到结构优化的目的。
[1]JGJ 120—99,建筑基坑支护技术规程 [S].
[2]徐日庆.考虑位移和时间的土压力计算方法[J].浙江大学学报(工学版),2000,34(4):370-375.
[3]邓子胜.深基坑支护结构-土空间非线性共同作用研究[D].长沙:湖南大学,2006.
[4]徐扬青.深基坑支护结构的优化设计计算 [J].岩土力学,1997,18(2):57-61.
[5]朱建新,付玉华,张耀平.排桩-单支撑支护结构优化设计及应用[J].南方冶金学院学报,2004,25(1):58-61.
