纵向加劲钢箱梁桥的简化分析

张 慧，杨子江，刘世忠，吴 辉

（兰州交通大学，甘肃兰州 730070）

0 引言

为适应交通现代化的发展需求，一些高速公路桥梁开始向8车道发展，单幅桥梁的横向宽度不断增加。同时，随着对桥梁结构简化和施工方便的要求提高，国内外建造的连续梁桥中采用能适应较宽桥梁的大宽跨比、宽体、单箱多室宽箱截面形式者越来越多。这种桥梁具有腹板间距大、横向翼缘宽、箱壁薄等特点。薄壁箱梁从刚度、强度需要，经济考虑和减轻自重方面均被认为是一种有效的机构形式。尤其是当把正交异性板和钢箱梁结构形式两者结合到一起的时候，大跨径桥的板厚和自重都大大降低了[1]。

正交异性板除作为桥面外，还是主梁截面的组成部份，它既是纵横梁的上翼缘，又是主梁的上翼缘。传统的分析方法是把它分成3个结构体系加以研究：

（1）主梁体系。由盖板和纵肋组成主梁的上翼缘，是主梁的一部分。

（2）桥面体系。由纵肋、横梁和盖板组成，盖板成为纵肋和横梁的共同上翼缘。

（3）盖板体系。仅指盖板，它被视为支承在纵肋和横梁上的各向同性连续板。

正交异性板最重要的优点在于由于桥面板的3个阶段受力的共同作用而减轻了自重，目前在许多国家都采用此类梁结构。

本文通过模型试验和理论分析，评估了一种新型的正交异性板箱梁桥。其鱼腹式的箱型横截面可以满足城市中大宽跨比、大跨、抗风和外形美观的需要。该类型桥的特别之处不仅仅在于他们内在、外形和抗风，更重要的是对于结构材料和刚度的有效利用[2]。

本文根据两种不同的简化分析方法思路进行了该结构的分析计算，得到了相应的计算结果，并与实际的全桥模型进行对比。虽然对于某些细节部位和连接部分应用有限元建立模型是不必可少的环节，但是理论分析对于设计计算过程中快速准确地确定内力和弯矩仍然是一种非常有效的方法。

综上所述，本文在建立大比例模型试验的基础上，分析大宽跨比宽体鱼腹式薄壁钢箱梁应用于连续梁桥时的空间力学性能，为大宽跨比宽体鱼腹式薄壁钢箱梁在连续梁桥上的准确应用奠定理论基础。研究成果将对提高我国大宽跨比宽体鱼腹式钢箱梁结构工程科技水平具有积极的意义，应用前景十分广阔，并且将会产生很好的社会及经济效益。

1 原桥和模型

本文参照厦门市仙岳路桥制作了1∶8的大比例有机玻璃试验模型，桥式结构为一单箱三室的薄壁钢箱连续梁桥，其桥面板为正交异型板T型加劲肋。模型梁桥跨布置为：4.5m+4.5m的两跨箱形连续梁（见图1）。模型截面尺寸示意图见图2。全桥共设置9处横隔板。支座位于梁的两端和中间支点处，每排对称布置两个。

采用的有机玻璃板的厚度有：1m m、1.5m m、1.8m m、3.5m m四种类型。

2 分析方法

图1 试验模型

图2 模型截面尺寸示意图（单位：m）

钢材是一种各向同性材料，然而一块弹性的正交异性板是由一块薄板和纵向以及横向加劲肋所组成，由于纵横向刚度是不同的，从而形成了一种结构的各项异性板。因此，本文构造一块各项异性的薄板，此板在纵横向上的弹性性能不同，大小分别与正交异性板的两个正交方向的性能一致(见图3)。

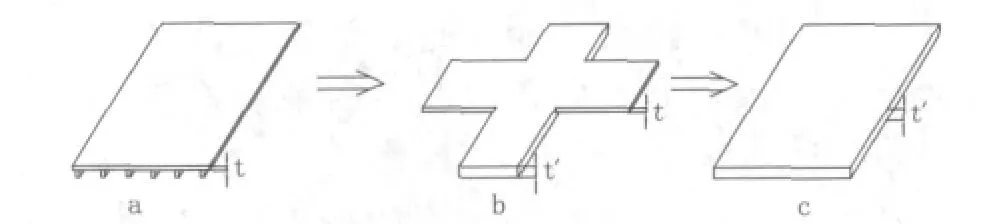
图3 转换过程图

对于钢板的理论分析，考虑到将其简化为薄壳结构，因此此类分析可以分为两类问题：平面应力问题，薄板弯曲问题。

2.1 平面应力问题

以本文所示桥型为研究对象，该桥面板只有纵向加劲肋，该桥原桥面板厚度为t，如图3（a）。首先假定一个简化正交异性板厚度纵向厚度为t′，横向为t，如图3（b)。为了简化分析，横梁的影响忽略不计。因此，该板纵向单位拉压刚度为E·t′，横向为E·t。其次，保持刚度不便，将其简化成一块厚度为t′，如图3（c)各项异性板。令Ex=E，那么纵向单位拉压刚度为 E·t′；令 Ey=E·，横向为E·t。很容易可以发现此板与前面的正交异性板具有相同的刚度。因为，所以令μx=μ，那么μy=μ·。

2.2 薄板弯曲理论

本文以薄板的小挠度弯曲理论为基础，设原来板的厚度为t。首先，假定一个正交异性板在纵向厚度为h，横向板厚为t。那么单位纵向抗弯刚度变为E·，横向为E·。其次，构造一个各项异性板与此板具有相同的刚度，板的厚度为h。令Ex=E，那么单位纵向抗弯刚度E·；令Ey=，那么横向为 E·

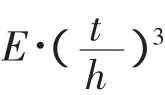
3.3 薄板弯曲理论(Method 3)

根据上面的分析，加劲肋的总的弯曲刚度保持不变，那么

E·I′=E·∑（I肋+A肋·y2）

通过保持相等的惯性矩，纵向的加劲肋可以被均匀分布到整个桥面板。令板的厚度为h(h是通过加劲肋转换的板的厚度)，因

μx=μ，那么。

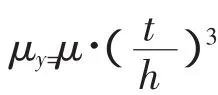
3 有限元模型

3.1 全壳模型(Method 1)

采用She ll63单元模拟全桥的桥面板和加劲肋[3]。单元总数为22496，节点数为 22574，图4为全壳模型细部图。

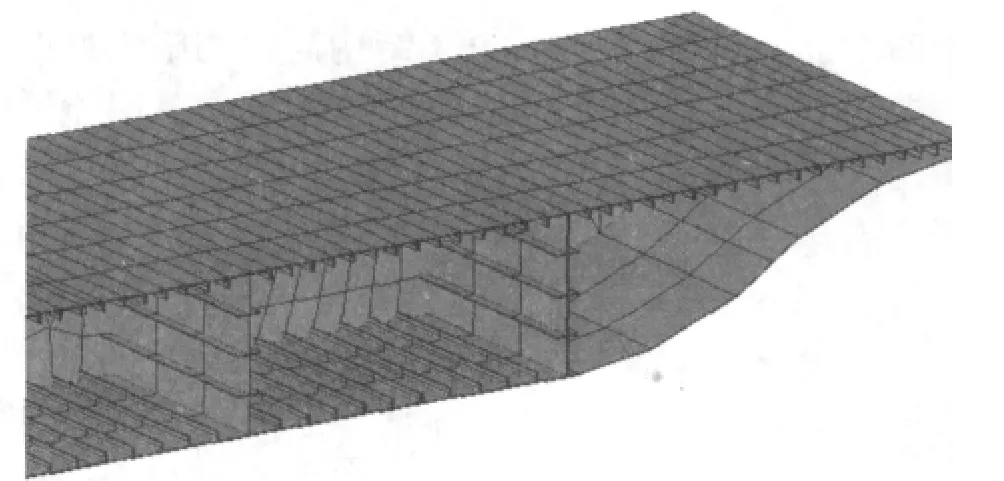
图4 全壳模型细部图

3.2 平面应力理论(Method 2)

根据上面的理论分析，通过保持相等的惯性矩，纵向的加劲肋可以被均匀分布到整个桥面板。板厚为。采用She ll63单元，单元总数为12870，节点数为13078。图5为平面应力理论模型细部图。

图5 平面应力理论模型细部图

故

采用She ll63单元，单元总数为12870，节点数为13078。

3.4 壳梁单元组合(Method 4)

另外一种简化建模的方法是，用壳单元模拟薄板板，用梁单元来模拟加劲肋的作用[4]。 单元总数为21654，节点数为13046。图6为壳梁单元组合模型细部图。

图6 壳梁单元组合模型细部图

4 模型试验

4.1 材料试验

有机玻璃材料性能指标主要是弹性模量和泊松比。试验采用制作模型的同一批材料，拉伸试件是采用粘贴双向应变片于试件测点位置上下侧，以测定其轴向应变和横向应变，进而确定其拉伸弹性模量和泊松比。经过测量和计算，有机玻璃的实测弹性模量E=2.65G Pa，泊松比μ=0.3505。

4.2 控制截面和测点确定

（1）静态应变控制截面。根据桥跨结构模型试验检测的目的并考虑测试控制、数据采集、布点、布线工作的方便，同时利用结构的对称互等原理，测试应变控制截面如图7所示。

图7 应力测试截面布置图

（2）静态应变测点布置。每截面共布设2 8个应变片，3个检测断面共布设8 4个应变片。各截面应变测点布置见图8。

（3）静态挠度控制截面及测点布置。分别在左跨L/2、L3/4底板下缘各布设4个位移测点；右跨L/2截面的底板下缘布设3个位移测点，总计1 1个位移测点。图9为位移测点布置图。

图8 截面1、2、3应变测点布置图

图9 位移测点布置图

5.2 位移

4.3 加载

加载位置如图1 0所示。

图10 加载位置图

5 结果分析与比较

5.1 结果分析比较

4种方法的单元节点总数比较图见图1 1。

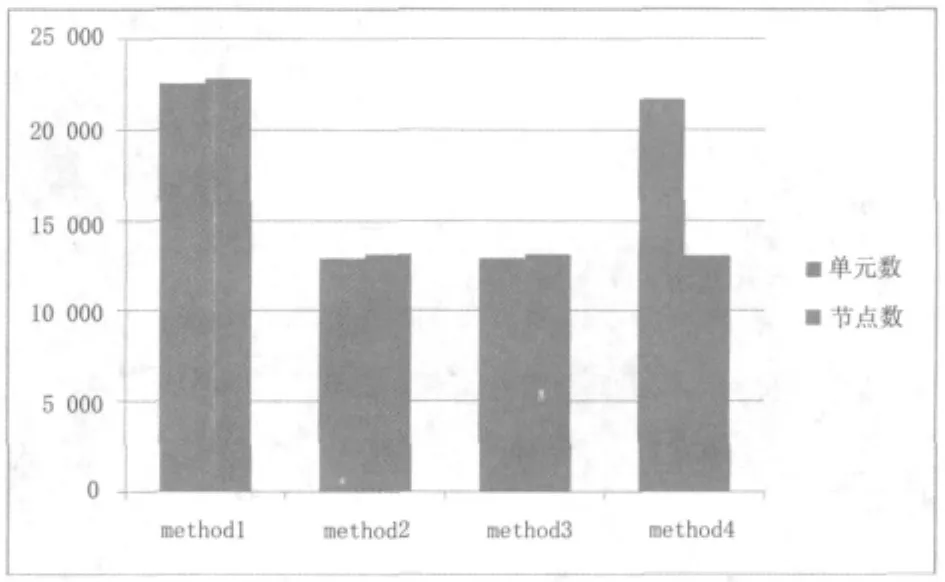
图11 4种方法的单元节点数比较

图12为工况下挠度比较。

图12 工况下挠度比较

总的来说，试验的挠度结果与3种方法的计算结果吻合很好，但偏大。这主要由于模型材料的不均匀和测试误差造成的。此外有机玻璃的粘接会在一定程度上降低有机玻璃的弹性模量，这也会造成试验结果与计算之间的偏差。

5.3 应力分布

5.3.1 截面一应力分布

截面一位于左跨跨中位置，其顶底板正应力分布的计算值和试验值如图1 3所示。从顶板图中可以看出全壳模型（Method1）与测试结果吻合良好。证明全壳模型是模拟结构最好的一个方法。比较其他几种方法，薄板弯曲理论（Method3）与全壳模型（Method1）最接近。事实上这是由于截面一的位置处于荷载作用处和横隔板附近，因此该处由于局部加载所产生的局部弯曲效应非常明显。此时，由于薄板弯曲所产生的二次应力非常明显，用薄板弯曲理论（Method3）进行分析较其他方法更为适合。也因为同样的原因，平面应力理论（Method2）的计算结果与实际情况相差很远，甚至已经超出了材料的极限强度。此外，薄板弯曲理论（Method3）较壳梁单元组合（Method4）在应力分布的形状和数值上都更接近于全壳模型（Method1），但是单元数只有后者的一半。以此类推，如果模型较复杂的时候，无论在建模时间和计算工作量上都能大大地节约，从而起到了简化模型的目的。

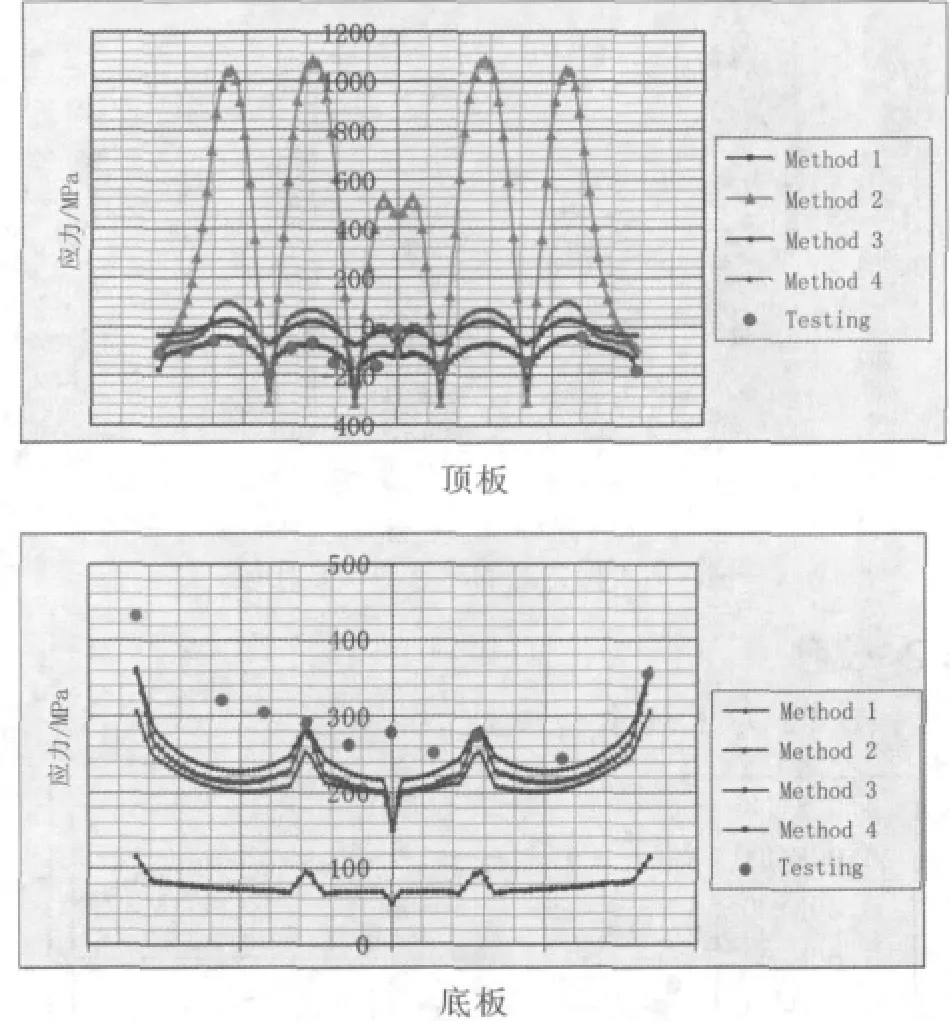
图13 截面一应力分布

从图13的底板应力分布情况可以看出，除了薄板弯曲理论（Method3），其他方法的结果都与试验结果比较接近，都能反映出应力的分布情况和桥梁的特点。

5.3.2 特殊截面应力分布

由于顶板受到加载和横隔板影响，所以不能真实地反映出整个梁体的整体应力分布情况。考虑的横隔板的弹性约束、加载效应分布和圣维南原理，本文选择一个特殊截面，该截面位于两个横隔板之间，远离加载位置，与左侧两端距离3m（见图14）。从图15可以看出，除了薄板弯曲理论（Method3）其他的方法都比较接近实际情况。

图14 特殊截面位置示意图

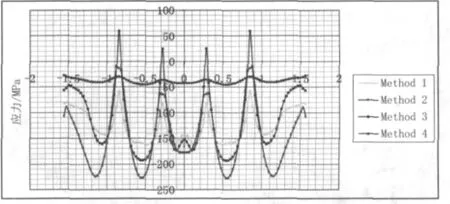
图15 顶板应力分布

总的来说，加载位置和弹性约束是分析顶板应力分布的关键因素。

6 结语

本文就一鱼腹式单箱多室薄壁连续钢箱梁桥进行研究。有限元建模有其优点，但是文中所研究的分析方法还是有其优势，尤其是在梁的初步设计中。虽然全壳模型在分析计算中较为可靠，然而如果模型过大和复杂，太多的单元和节点增加了建模和计算的困难。薄板弯曲理论（Method3）对于分析荷载作用点和横隔板附近的局部结构问题相比于其他的方法是最有效的一种。对于简化分析，平面应力理论（Method2）和壳梁单元组合（Method4）可以用在受加载和横隔板影响较小的截面，对于底板分析，两法均可适用，其中壳梁单元组合（Method4）比平面应力理论（Method2）结果更接近实测值，但建模计算工作量稍大。在整体主梁挠度分析中，除了薄板弯曲理论（Method3）其他均适用。

致谢：项目由国家自然科学基金（Grant No.50968008）以及河北青银高速公路管理处研究项目资助。

[1]Vlasov VZ.Thin-walled elastic beams[M].Washington,DC:National Science Foundation，1961.

[2]Hui Zhang,R.DesRoches,Zijiang Yang,Shizhong Liu.Experimental and analytical studies on a streamlined steel box girder[J].Journal of Constructional Steel Research，2010（66）：906-914）.

[3]Paolo Lisandrin.Elements of Automated Aero elastic Analysis inAircraft Preliminary Design[M].Delft University of Technology:Faculty of Aerospace Engineering，2007.

[4]KISSK,DUNAI L.Stress History Generation for Truss Bridges UsingMulti-lever Models[J].Computers & Structures,2000,78(1):329-339.