准晶简述——2011年度诺贝尔化学奖

孙俊良

(北京大学化学与分子工程学院 北京 100871)

瑰丽多彩的具有规则外形的晶体一直是人们乐于收集和欣赏的对象，如各种宝石，钻石等(图1)。为了了解这些晶体的内在本质，人们在17世纪就开始了晶体学方面的研究，但早期的晶体学局限于几何外形和一些假说上。随着1912年X射线晶体学的诞生，晶体学得到了迅速发展，并连续获得了诺贝尔奖(如Max von Laue，1914年诺贝尔物理学奖；William Henry Bragg和William Lawrence Bragg，1915年诺贝尔物理学奖)。其后晶体学被应用到各种物理学、化学和生物学领域，逐渐发展成为一种非常完备、无可辩驳的描述物质结构的方法。

传统的晶体学理论遇到的唯一也是最大的挑战就是Dan Shechtman在1982年发现的Al-Mn合金急冷相中准晶[1]。准晶所具有的5次对称性(图1)从根本上改变了人们对晶体的看法，晶体的定义也因此被改写。

图1 普通的具有三维平移对称性的晶体(绿宝石Be3Al2(SiO3)6)和十二面体准晶单晶(ZnMgY体系)的照片

1 准晶的发现

在准晶发现之前，为了区别于非晶，晶体的一般要求是该固体具有规则外形，而其内部结构中的原子、离子或分子在空间排列成具有三维周期性的格子。根据这个定义，传统的晶体学理论在19世纪就已基本发展完善，它包括7个晶系，14种Bravais格子，32种晶体学点群以及由此得到的230个空间群[2]。这一理论在20世纪初被X射线晶体学所“证实”。然而这一传统定义的最大缺陷是把原子排列有序和三维周期性混为一谈，因为从一个更自然的角度，非晶与晶体的区分在于其内部结构中的原子、离子或分子是否呈有序排列，而有序是否会导致三维周期性在没有被证实的情况下作为常识被默认了。由于三维周期性的限制，传统定义的晶体中只能出现2、3、4、6次旋转轴，其他如5次以及6次以上的旋转轴被认为是禁止的。

虽然在X射线晶体学诞生不久，人们就发现了非共度相的存在，并在某种程度上否定了三维周期性对晶体的必要性，但是最初发现的两种非共度相都可以看成具有三维周期性的晶体的衍生结构。非共度调制结构可以看成是三维周期性的晶体中部分原子的位置、占有率或元素类型发生不同于原有晶体周期的有规律变化(图2a)，而非共度共生化合物则可以看成两个或多个具有不同三维周期性的晶体在原子尺度上的叠加(图2b)。因此，人们依然把结构有序和三维周期性看成是必须同时存在的现象。当Dan Shechtman发现准晶时，晶体学界展开了激烈的辩论，其焦点就是三维周期性是不是结构有序的必要条件。

图2 两种非共度结构的示意图(a) 非共度调制结构;(b) 非共度共生化合物。

Dan Shechtman最初是利用透射电子显微镜观察到了电子衍射图的10次对称性(图3)，其在正空间中可以对应于5次对称性，而这与晶体的三维周期性是不可共存的。由于坚持这样的研究，他面临了嘲笑并被所属研究团体要求另谋高就。而在文章发表之后，则被以两次诺贝尔奖获得者Linus Pauling为代表的科学家们评为“准科学家”，Pauling认为准晶其实是普通晶体按五次对称性生成的孪晶现象。但随着其他研究组类似化合物的报道，如中国已逝院士郭可信的研究组发现的10次准晶[3]，法日科学家在实验室成功合成出的可以用X射线研究的准晶[4]，以及深入研究从实验和理论上否定了五次对称性孪晶现象对准晶电子衍射图的解释，Dan Shechtman的准晶说法终于获得了科学界的认可。最终在1992年，晶体的定义“拥有规则有序，重复三维图案的固体”被改写为“衍射图谱具有明确图案的固体”。

图3 Dan Shechtman观察到的电子衍射图的10次对称性及1982年4月8日的实验记录

Dan Shechtman的努力最终迫使科学界反思对物质结构的认知，对物理学、化学和生物学的发展都有举足轻重的意义，也鼓舞了更多的科研工作者进入这一领域。虽然准晶最初是从急冷亚稳相中发现的，但热力学稳定的准晶相也很快就被合成出来，科研人员甚至在俄罗斯一条河流的矿物中发现了天然的准晶Al63Cu24Fe13[5]。由于特殊的原子位置排列，准晶也具有一些特殊的性质，如低的电导和热导、硬度高、抗腐蚀性强。准晶作为不沾锅涂层和医疗用手术针头已得到了应用，更多的(如在柴油发动机，催化，热电等方面)应用正在进一步开发中。

2 准晶的结构描述

尽管准晶没有三维周期性，但其之所以被认为是晶体，最根本的原因是它的原子排列是有序的。接下来的问题就是何为有序。从直觉上说，有序就是原子按某种规律排列，这种规律不一定是三维周期性；从数学上说，有序就是结构中的电子云密度函数可以用有限个基矢量进行傅立叶展开。传统的晶体具有三维周期性，其电子云密度函数只需要3个基矢量就可以展开，也就是说它的电子衍射或X射线衍射中的衍射点可以用3个基矢量指标化。对于图3中准晶的衍射图，则需要用4个基矢量才能够用整数指标化所有的衍射点，而整个三维的十二面体准晶需要6个基矢量才能描述。这样的晶体在三维空间中不具有平移对称性，但是在六维空间中，它们就具有平移对称性了。这里我们将不详细讨论准晶的超空间群描述，而是从简单的模型去理解准晶的结构和它们形成的机理。

2.1 Fibonacci链

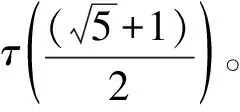
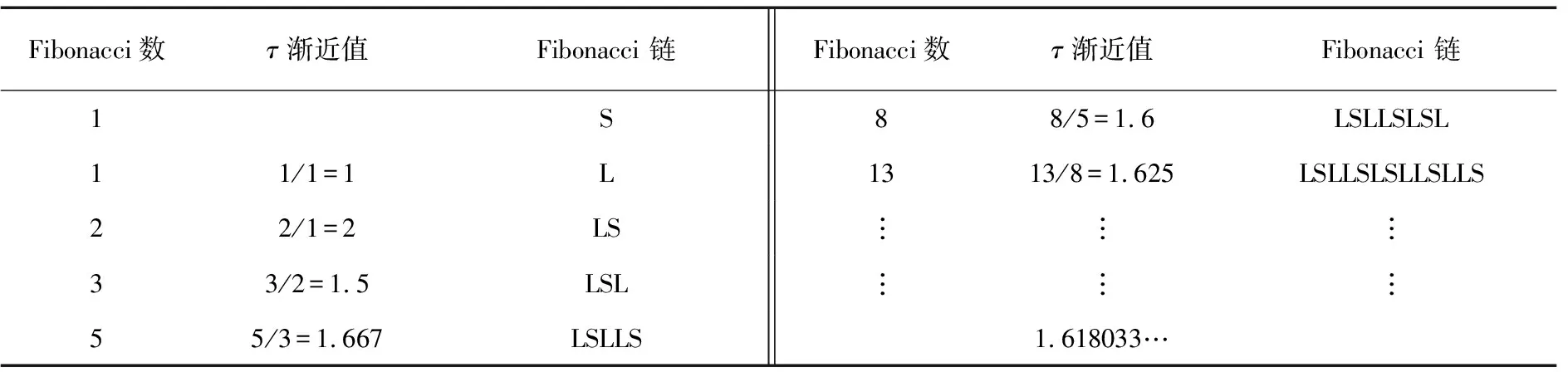
表1 Fibonacci 数和它的形象表示

2.2 Penrose拼砌

图4 由宽、窄两种菱形形成的Penrose 拼砌可以铺满整个二维平面，形成的衍射图案具有5次对称性。

二维准晶的结构可以用二维Penrose拼砌来理解。该拼砌由宽、窄两种菱形形成(图4)，分别具有36°和72°锐角。而真实的结构可以是对宽、窄两种菱形的修饰，整个结构可以认为是两种单胞在二维空间中按自相似原则的有规律排列。三维准晶的结构可以用三维Penrose拼砌来理解，它们由宽、窄两种菱面体堆砌而成[6]。

2.3 高维空间晶体学

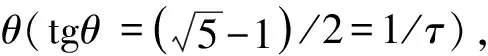
图5 由二维空间投影得到的一维准晶Fibonacci链

最后需要提到的是，虽然准晶理论已经发展了近30年，但准晶中原子位置的准确确定依然非常困难。这主要是因为准晶晶体一般都含有非常多的缺陷，并经常与其近似相共存。除了前面提到的利用超空间群确定结构和正空间利用堆砌建模型，人们也发展了从倒易空间相似性确定其结构[7]，这些方法一般都用于处理相对比较理想的准晶体系。对于缺陷更多的体系，则需要利用漫散射来得到phason mode的信息[8-9]。相信在2011年诺贝尔化学奖之后，会有更多的人参与到准晶的研究工作中，逐渐揭开其原子位置之谜，并把它更多地利用到实际应用中。

参 考 文 献

[1] Shechtman D,Blech I,Gratias D,etal.PhysRevLett,1984,53:1951

[2] Hahn Th.International Tables for Crystallography Volume A.5th ed.New York:John Wiley & Sons,Inc,2002

[3] 郭可信.准晶研究.杭州:浙江科技出版社出版,2004

[4] Fisher I R,Islam Z,Panchula A F,etal.PhilMagB,1998,77:1601

[5] Bindi L,Steinhardt P J,Yao N,etal.AmMineral,2011,96:928

[6] Rakakura H,Gómez C P,Yamamoto A,etal.NatureMater,2007,6:58

[7] Li M,Sun J,Oleynikov P,etal.ActaCrystB,2010,66:17