基于DSP的改进SVPWM算法
2012-09-25姜华杰王忠庆任一峰郭名君
姜华杰,王忠庆,任一峰,郭名君
(中北大学 信息与通信工程学院,太原 030051)
引 言
在电气传动领域中,交流调速占据着极其重要的地位。其先进的控制策略使交流变频调速系统正在逐步取代着结构复杂的直流调速系统。在交流调速系统中,运用最广泛的就是SPWM(正弦脉宽调制)和SVPWM(电压空间矢量PWM)。两者的出发点不同,SPWM调制是从三相交流电源出发,目的是生成一个可以调压调频的三相对称正弦电源。而SVPWM是将逆变器和电动机看成一个整体,根据确定位置的有限个空间矢量组合作用,来产生满足任意位置和一定幅值范围需要的空间矢量过程,即在整个PWM周期内改变各相导通时间的分配来形成所需要的任意空间矢量。
本文介绍一种改进的SVPWM算法,不同于以往的6扇区算法,而是分成12个扇区,低速转矩脉动更低、性能更稳定。
1 SVPWM基本原理及实现
SVPWM的理论基础是平均值等效原理,即在一个开关周期内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。
假设直流母线电压为Udc,逆变器输出的三相电压分别为UA、UB、UC,依次加在空间上互差120°的三相平面静止坐标系上。Um为相电压有效值,f为电源频率,并定义三个电压空间矢量 UA(t)、UB(t)、Uc(t),它们的方向始终在各相的轴线上,大小按正弦规律随时间变化,时间相位互差120°,则:
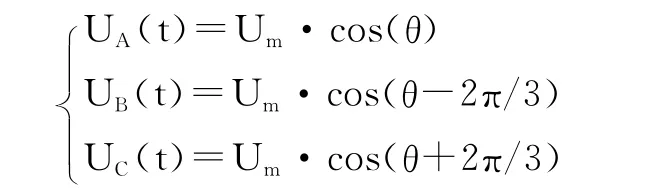
其中,θ=2πft,那么三相电压空间矢量相加的合成空间矢量 U(t)可表示为:
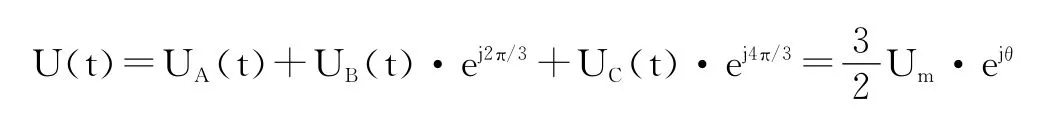
由上式可见,Ut是一个以角频率ω=2πf按逆时针方向匀速旋转的空间矢量,幅值为相电压峰值的1.5倍,Um为相电压峰值,而空间矢量Ut在三相坐标轴(a,b,c)上的投影就是对称的三相正弦量。
三相桥臂示意图如图1所示。由于逆变器三相桥臂共有6个开关管,为了方便研究各相上下桥臂在不同开关组合时逆变器输出的空间电压矢量,定义开关函数Sx(x=a、b、c)为:

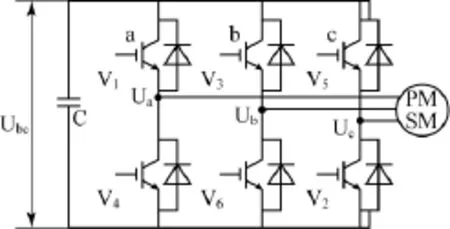
图1 三相桥臂示意图
(Sa、Sb、Sc)全部可能的组合共8个,包括6个非零矢量和2个零矢量。电压空间矢量如图2所示,给出了8个基本电压空间矢量的大小和位置。
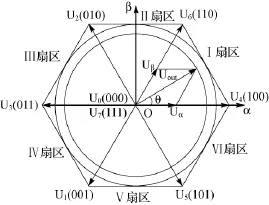
图2 电压空间矢量
图2所示任意两个相邻的非零矢量间隔为60°,并且幅值都相同(模长为2Udc/3),有两个位于中心的零矢量幅值为零。在每一个扇区,选择相邻的两个电压矢量以及零矢量,按伏秒平衡的原则合成每个扇区内的任意电压矢量,即:
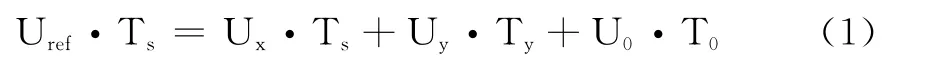
其中,Ts为采样周期;Uref为期望电压矢量;Tx、Ty、T0分别为对应的两个非零电压矢量Ux、Uy和零电压矢量U0在一个采样周期的作用时间;其中U0包括了U0和U7两个零矢量。式(1)表示,矢量Uref在T时间内所产生的积分效果值和 Ux、Uy、U0分别在时间 Tx、Ty、T0内产生的积分效果相加总和值相同。
在两相静止参考坐标系(α,β)中,令Uref和U1间的夹角是θ,按照正弦定理有:
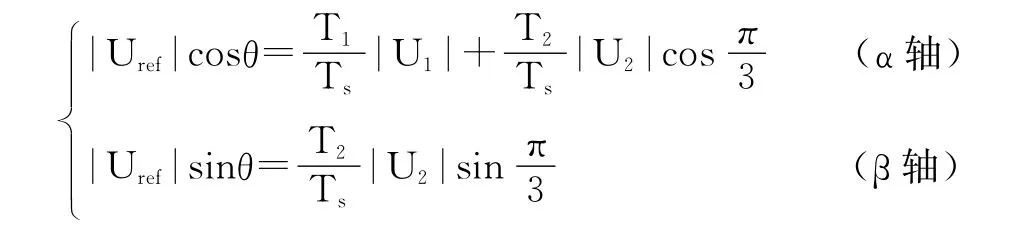
因为|U1|=|U2|=2Udc/3,到各矢量的状态保持时间为:
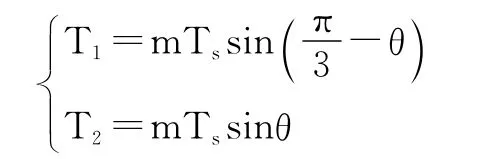
其中m为调制系数(调制深度),可表示为:
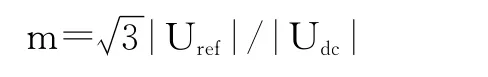
而零电压向量所用的时间为:
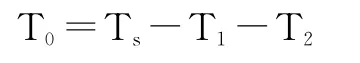
得到合成的Uref的时间后,接下来的问题就是如何产生实际的脉宽调制波形。在电压空间矢量调制方案中,零矢量的选择具有较高的灵活性,合理地选择零矢量,可最大限度地减少开关次数,尽可能避免在负载电流较大的时刻的开关动作,这样可以最大限度地减少开关损耗。
以往的算法都是分6个扇区,并且在赋值之前要先判断目标矢量位于哪个扇区,一方面由于分区较少,划分不够精准,在低速时抖动比较明显;另一方面在程序上比较繁琐。这里提出一种不同于与以往的6扇区的算法,根据角度步距计算得到的实际角度值除以30°,商为扇区编号,余数经过处理之后就是扇区角了,新扇区示意图如图3所示。
对余数的处理,分两种情况。以前两个扇区为例,若商为奇数(即在1、3、5、7、9、11扇区),则所得余数加上30°即为输出电压矢量所在扇区对应的扇区角;若商为偶数(即在0、2、4、6、8、10扇区),则所得余数就是该扇区所对应的扇区角。另外,提前计算清楚不同扇区需要赋值的情况,并编成表格,在后面的赋值中直接根据表格代入,免去了每次判断扇区的麻烦,形式上更为简捷。部分程序代码如下:
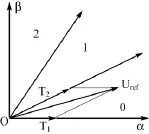
图3 新扇区示意图



2 软件设计
系统上电后开始初始化,包括时钟和锁相环的设置以及I/O口的初始化、中断初始化、变量初始化等。然后进入主程序,主程序中主要进行有关参数的初始化配置和定标,在主程序中循环等待定时器的定时时间的到来,主要计算工作在定时器下溢中断中进行。主程序流程如图4所示。
当定时时间到来时,进入定时器中断程序,整个波形的计算及更新3路比较寄存器的程序是放在通用定时器1的中断当中的,在确定出调制深度和扇区角及扇区编号之后,代入公式计算出基本矢量作用时间T1和T2,并根据不同扇区赋给相应的值。定时器下溢中断流程如图5所示。
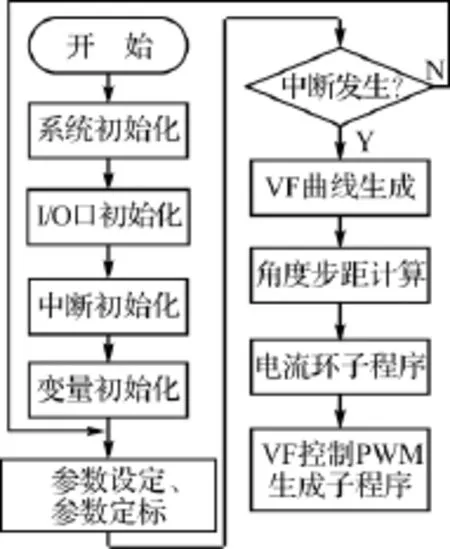
图4 主程序流程

图5 定时器下溢中断流程
3 运行结果
运行方波如图6所示。截取了几个周期波形,未滤波之前的波形清晰稳定,周期性明显,符合理论预期。
阻容滤波后得到的马鞍波如图7所示。

图6 运行方波

图7 滤波后得到的马鞍波
在低速状态下,波形基本为标准的马鞍波,波形平滑均匀,并且已经带电机运行,实测性能比较稳定,转矩脉动很低,取得了预期的效果。
[1]王宏民,赵振民,李娜.SVPWM算法在TMS320F2812上的实现[J].煤矿机械,2008,29(10):42-44.
[2]张少伟.SVPWM在有源逆变中的研究与应用[D].保定:华北电力大学,2008:17-30.
[3]苏奎峰,吕强,邓志东,等.TMS320x28xxx原理及程序开发[M].北京:电子工业出版社,2009:314-331.
[4]胡庆波,吕征宇.一种新颖的基于空间矢量PWM的死区补偿方法[J].中国电机工程学报,2005,25(3).
[5]D G Holmes,Thomas A Lipo.Pulse Width Modulation For Power Converters[M].Hoboker:Wiley-IEEE Press,2003.
