武咸城际铁路基准点沉降对监测点影响改正模型研究
2012-09-22王俊丰花向红刘金标叶珉吕
王俊丰 ,花向红,刘金标,叶珉吕
(1.武汉大学测绘学院,湖北武汉 430079; 2.武汉市勘测设计研究院,湖北武汉 430022;3.武汉大学灾害监测与防治研究中心,湖北武汉 430079)
1 引言
通常进行沉降观测时,一般认为基准点是固定不动的,但实际上,基准点并非是一直恒定不变。当基准点位于沉降区域内,它就有可能发生变动。如果基准点发生了变动,在进行沉降观测平差计算时不加以考虑,就会产生不正确的结果[1]。另一方面,基准点稳定性是通过一般半年或一年一次复测获取的,而沉降监测点监测按照规范要求和工程情况确定监测周期,这样,如果基准点发生变化,而在监测点的沉降中没有考虑,会与实际情况有所出入,导致监测点沉降出现异常情况,这对工程施工或运营状况,不能做出正确的判断,而产生比较严重的后果,因此,有必要对考虑基准点沉降对监测点影响进行研究,提出改正办法。为此,本文提出了基准点沉降下的监测点改正模型,并通过武咸城际铁路实际数据进行计算分析,得出了有益的结论。
2 基准点沉降对监测点影响改正模型
根据武咸城际铁路桥梁、路基、涵洞、隧道、过渡段沉降监测实际情况,沉降监测一般以经过两个基准点构成的沉降监测网。特殊情况下,可以经过一个基准点构成的沉降监测网,图1为武咸城际铁路桥墩沉降监测网示意[2]。
如图1所示,设A,B为两个基准点,在A,B中间存在一系列的沉降监测点 ik(k=1,2,…,n -1,n,其中n为监测点个数),在时刻T0,通过基准网复测可以得到A,B两点的高程,设为,在时刻Tn通过控制网复测有又可以得到A,B两点的高程,设为由于相邻两次基准网之间存在一定的时间间隔△T,通常为半年。如果不等于等于,即基准点发生沉降时,必须考虑基准点变化的影响,对监测点ik的高程(或沉降量)进行改正[4]。
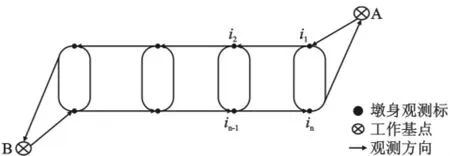
图1 桥墩沉降监测网
2.1 高程改正方法
高程改正方法的基本思想[5]是,首先,需要求出基准点在任意时刻为T(T0<T<Tn)的高程。方法是假定基准点的沉降速度是恒定的,由此得到:A点的沉降速度为:

从而可以得到A,B两点任意时刻T的高程为:

采用这种方法,要分别计算不同时段基准点的高程,需要对整个桥墩沉降监测网进行平差计算,没有利用已有的计算成果,大大增加了数据处理计算的工作量。
2.2 沉降量改正方法
实际工作中,在计算每期监测点高程(或沉降量)时,一般以首次高程基准的成果进行处理,得到了各期监测点的沉降量△hik,经过基准复测后,基准点发生变化,需要对前面各期沉降监测点沉降量进行改正[6]。方法是假定监测点由基准点沉降引起的修正沉降速度与到起始基准点的距离相关,即:

式中Si为任意监测点到起始基准点的距离,VA,VB如式(1),式(2)所示。
则T时刻任意点ik的沉降改正数为:

T时刻任意点ik沉降量为△hik+δik,即未改正的沉降量加上沉降改正数。
3 工程实例计算与分析
为了考察本文提出的基准点沉降下的监测点改正模型的有效性,本文对武咸城际铁路某段桥梁墩台的沉降进行实验计算。
武咸城际铁路武汉至纸坊段沉降监测基准网从2010年11月开始测量至2012年3月已测量了4次,使用仪器为徕卡DNA03,而该段桥墩施工是在不同时间进行的,因此,各桥墩首次监测的时间也不相同。限于篇幅,这里只对 Z18-1、Z18-2、Z20-1、Z20-2、Z22-1、Z22-2桥墩的沉降情况进行分析,这些桥墩监测点是从2011年4月开始监测,施测这些桥墩所用的基准点为GWX050与GWX051,以2011年4月数据为起始数据,由此计算各监测点未考虑基准变化的高程数据和沉降量数据,如表1、表2所示。

部分监测点未考虑基准变化的高程数据/m 表1

部分监测点未考虑基准变化的沉降量数据/m 表2
根据复测资料,GWX050与GWX051两点各期高程如表3所示。

期基准网复测成果表/m 表3
由表1、表2可以看出,桥墩存在一个上升的趋势。由表3可以看出,2011年11月与2011年4月相比,从数值上讲GWX050上升了0.5 mm,而GWX051下降了6.1 mm,根据复测成果,两次复测GWX050高程中误差分别为0.4 mm、0.5 mm,两次较差中误差为0.6 mm,两次复测 GWX051高程中误差分别为0.5 mm、0.6 mm,两次较差中误差为0.8 mm,因此,可以认为 GWX050没有变化,是测量误差引起的,但GWX051数值上较大,点位发生了沉降,因此,如果在计算桥墩沉降时并没有考虑基准点沉降对监测点影响,会导致监测点沉降量出现可能不符合实际情况,对后续分析判断工作带来麻烦,因此有必要考虑基准点沉降对监测点影响,并加以改正。
按照本文所给出的模型,考虑基准变化,其结果如表4~表6所示。

高程改正方法所得的高程结果/m 表4

高程改正方法所得的沉降量结果/mm 表5
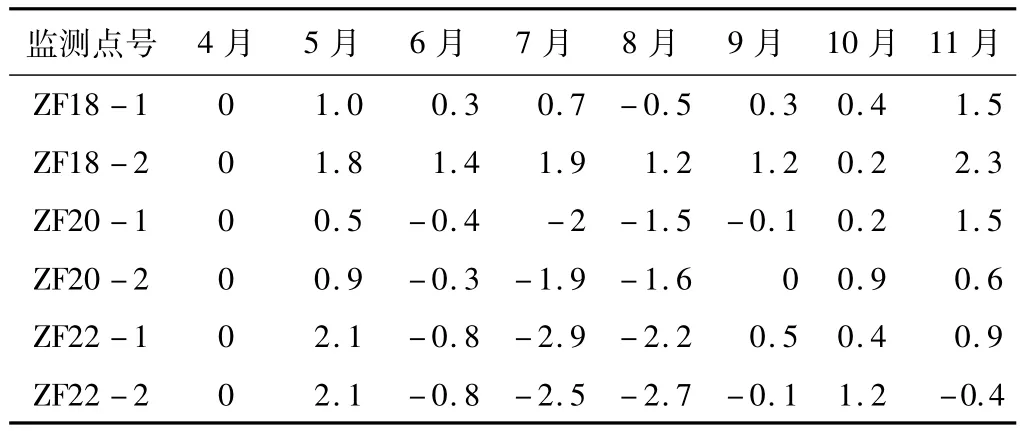
沉降量改正方法所得的沉降量结果/mm 表6
为便于比较,画出了6个点的沉降过程线,如图2~图7所示。
由表4~表6可以看出:使用本文所提出的两种方法进行改正,监测点的沉降量数值上减小,与附近的桥墩相比,经过改正后能较好的反应桥墩实际沉降情况。相对于2011年11月,高程改正方法所得沉降量最大上升1.5 mm,沉降量改正方法所得沉降量最大上升2.3 mm。
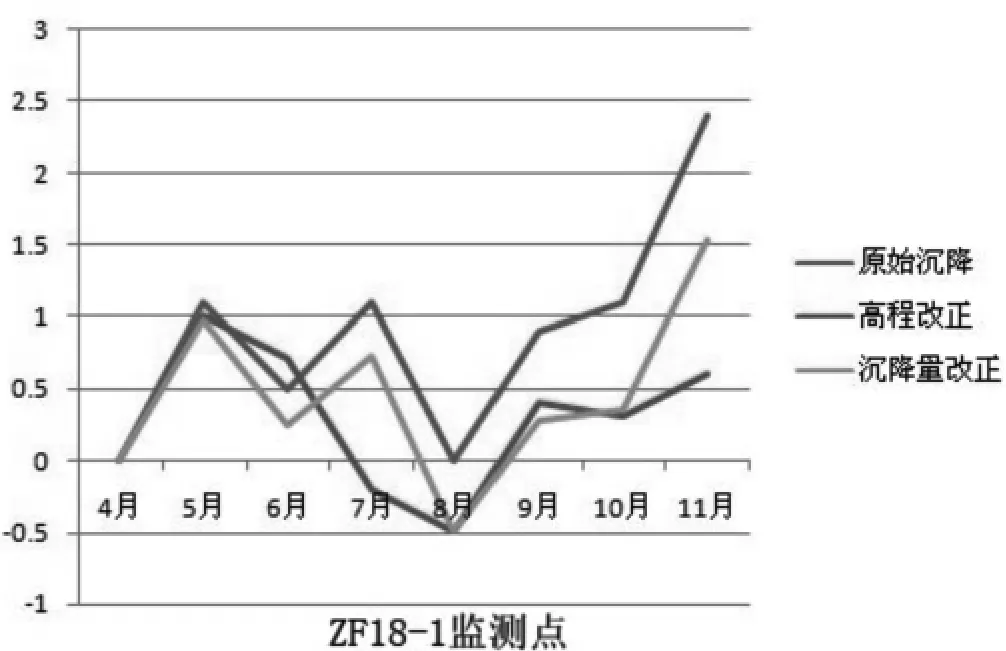
图2 ZF18-1沉降过程线
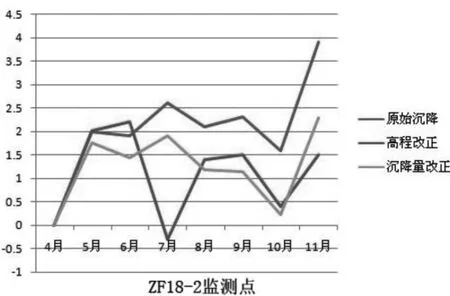
图3 ZF18-2沉降过程线
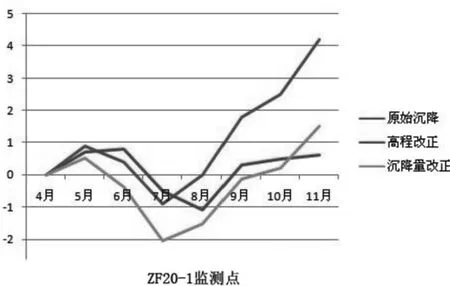
图4 ZF20-1沉降过程线

图5 ZF20-2沉降过程线

图6 ZF22-1沉降过程线

图7 ZF22-2沉降过程线
由图2~图7沉降过程线可以看出:沉降量改正方法相对于高程改正方法而言,沉降量改正方法与原始沉降的趋势基本相同,但高程改正方法与原始沉降之间存在一些差异,如ZF18-1,ZF18-2点在7月时两者之间的变化趋势完全相反。
4 结论
综上所述,本文所提出的两种改正方法是可行的和有效的,两种方法相比较而言,我们认为采用沉降量改正方法更有效,易于编程实现,而且可以很好地利用已有成果,减少计算处理工作量。当然本文提出的沉降量改正模型,还有待于进一步探讨,需根据工程情况,找出合适的改正模型。
[1]张正禄,李广云,潘国荣等.工程测量学[M].武汉:武汉大学出版社,2005:175~212.
[2]湖北城际铁路有限责任公司.武汉城市圈城际铁路沉降变形观测实施细则[R].2010.
[3]武汉大学测绘学院测量平差学科组.误差理论与测量数据处理[M].武汉:武汉大学出版社,2007:102~142.
[4]黄声享,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010:78~83.
[5]黄声享.监测网的稳定性分析[J].测绘信息与工程,2001(3):16~19.
[6]苏京平.控制网的稳定性分析[J].城市勘测,2000(4):14~16.
