GPS高程传递中天线相位中心垂直偏差的改正

2012-09-22黄纪晨

城市勘测 2012年6期

黄纪晨

(新疆交通规划勘察设计研究院，新疆乌鲁木齐 830006)

1 引言

GPS测量中，伪距观测值和相位观测值均以接收机天线相位中心位置为基准测定与卫星之间的距离，实测时天线的对中整平是以接收机天线的几何中心位置为基准，因此理论上设计接收机天线的相位中心应该与其几何中心保持一致。但是，实际上接收机天线的相位中心瞬时位置会随着信号输入强度和方向的不同而发生变化，即观测时相位中心的瞬时位置(称为视相位中心)与理论上的接收机天线的中心位置将有所不同。接收机天线的这种相位中心瞬时位置和设计位置的偏差就是天线相位中心偏差。天线相位中心的偏差会对相对定位结果造成定位误差，根据天线性能的优劣，甚至可达数毫米至数厘米，对于精密相对定位，这种影响是不容忽视的［1，2］。

2 天线相位中心偏差垂直分量的检测

GPS接收机天线相位中心偏差，包括水平偏差和垂直偏差两个方面，一般接收机天线的相位中心垂直方向上的偏差远大于水平方向上的偏差。GPS接收机天线相位中心偏差及其稳定性，是影响高精度GPS测量的一个重要因素。而GPS接收机天线相位中心垂直分量的偏差对于GPS高程测量精度的影响是非常明显的，在变形监测中以及常规测量中很容易产生较大误差，因此必须要采取一定措施予以削弱，以保证获得可靠的测量值［3］。

实际野外观测工作中，如果使用同种类型的同种型号的GPS接收机天线，因为是按照相同的设计标准、制作工艺和材料，所以相位中心偏差一般较小，可以认为是由于测量的误差、模型改正不完善或者计算误差等引起的，数据处理时作为偶然误差处理。如果在相距不远的两个或多个观测站上，同步观测同一组卫星，采用相对定位模式，可通过观测值求差来削弱相位中心偏移的影响。对于同种类型不同型号的接收机天线或者是不同类型的接收机天线进行组合观测时，相位中心偏差的垂直分量的差值较大，对GPS高程测量精度的影响远大于GPS平面测量精度，因此在高精度的GPS高程测量中应该尽量避免使用不同的GPS接收机天线，若使用则应利用改正方法来减弱或消除影响。

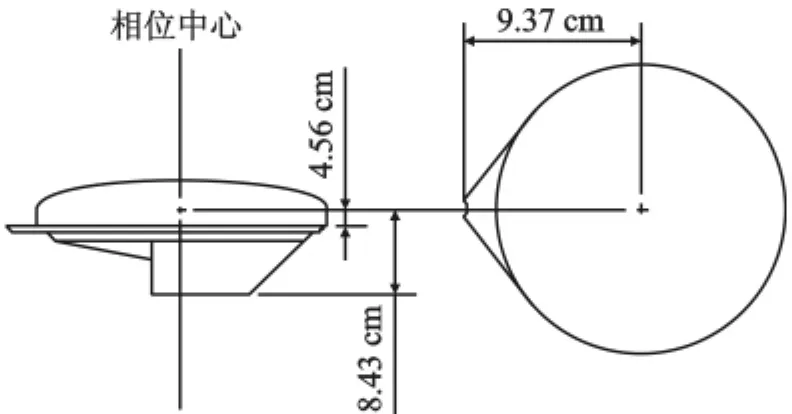
图1 天线相位中心示意图

GPS接收机生产厂家提供的天线相位中心的位置可以改正实测天线相位中心到测点的垂直高度(天线高)。图1是Trimble Zephyr Model 2天线相位中心示意图。基线解算时，要将这些数据提供给基线解算软件，以便获得可靠的结果。即使在解算时加入了天线相位中心的偏差改正，观测作业时的天线实际相位中心和厂家提供的几何中心并不完全一致，即观测时天线的相位中心的瞬时位置与理论的相位中心有所不同，这使定位结果存在着天线相位中心位置不准确的误差。因此，有必要采用有效方法以测定天线相位中心偏差。

现阶段，对于GPS接收机天线相位中心偏差垂直分量的测定方法有两种:一是用微波天线测量设备在室内测定;二是室外实验测定。

室内微波天线测量设备可以精确测定GPS天线相位中心偏差。微波天线测量设备包括1780系列可编程微波接收机、1581型方向图绘图仪、微波发射天线以及微波暗室等四部分。室内微波检定法测定GPS接收机天线相位中心偏差的测量精度，可以达1 mm～2 mm。但是微波暗室等相关设备复杂、昂贵，鉴定费用高，且一般生产部门并没有这些设备，不适用于实际测量工作中应用。在实际测量工作中，主要采用在室外检测GPS天线相位中心垂直分量相对偏差值，来消除天线相位中心偏差对高程的影响［4，5］。

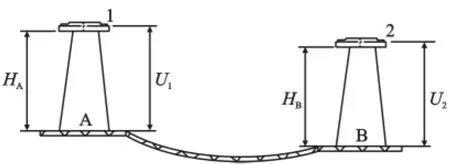
图2 相对相位中心检测示意图

在室外精确测定天线相位中心垂直偏差，必须得到测点的精确大地高或者待检测天线中有一台相位中心垂直偏差已经精确测得(可以用室内微天线测量设备测定)。大地高是无法精确测定的，因此室外一般采用交换天线法检测。在天空视野开阔、无强电磁干扰的室外，相距很近的距离(≤30 m)上设A、B强制观测墩且墩面严格水平，如图2所示，两墩之间的连接链表示相距很近的地面。在观测墩上直接安置两台GPS接收机进行相对定位观测。由于A、B两点距离短，两观测站上空的大气状况极为相似，电离层延迟和对流层延迟产生的误差以及其他误差源的影响也很相近，利用模型改正和差分改正可以削弱这些误差源的影响，因此近似地认为垂直方向上只存在天线相位中心偏差。且A、B两点相距很近，因此可以认为两点高程异常相等。设A点和B点的大地高分别为HA和HB，并设U1和U2分别为通过GPS基线解算求出的A、B两点上的大地高。A点上安置1号机，认为其相位中心偏差为h1;B点上安置2号机，认为其相位中心偏差为h2，h1和h2均包括正负号，测定位置在理论位置之上取正，反之取负。则有:

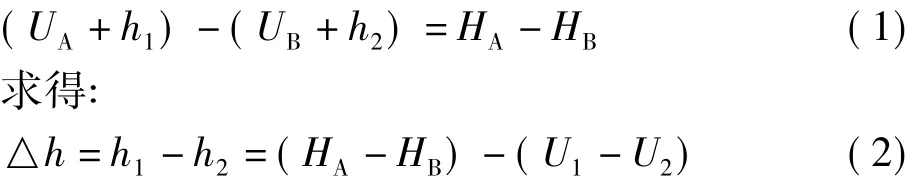
式中，(HA－HB)为A、B两点的大地高差，在相近的两点假设高程异常相等的情况下可以由精密水准测得。由此可得到两个天线的相位中心垂直偏差的差值，如果其中一台天线的相位中心垂直偏差已知则可求得另一台天线的偏差值。

若没有已知相位中心垂直偏差的GPS天线，则无法精确求得待求仪器的相位中心垂直偏差，但是在此方法的基础上加以改进依然具有实用价值。若待测两点间的距离较远时，虽然这时的高程异常并不能认为近似相等，但是仍能准确的测定两点间的大地高差。

图3 改进相对相位中心检测示意图

如图3所示，第一时段观测完后，将1、2号天线交换安置进行第二时段观测，根据两个时段分别列方程:

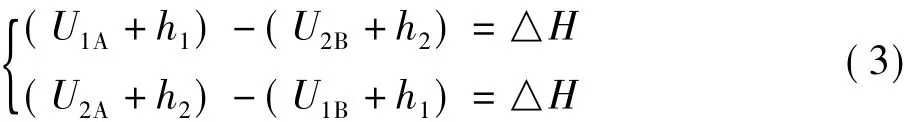
两式相加求得:

△H即是待测两点间的精确大地高差，在检验相位中心垂直偏差稳定性和改正小网观测大地高时具备了实际应用价值。

3 天线相位中心偏差垂直分量稳定性检测

GPS高程传递作业之前应该检验其相位中心垂直偏差的稳定性。虽然相位中心垂直偏差无法精确测定而不能直观判断其稳定性，但是可以通过两台GPS天线的相位中心垂直偏差之差来判断，并且差值可以作为两台天线相位中心垂直偏差的相对改正量。

现有GPS仪器4台，分别为Trimble R7 GNSS和Trimble R8 GNSS两种型号，实验场地设置在相距较远的两个强制观测墩上，墩面制作用水平尺严格水平。根据图3所示的交换天线法，每个时段观测45 min，两个时段为一测回，一测回之内交换仪器不停顿测量，测回之间休息1.5 h，采集的实验数据利用TGO和Cosa联合解算。则一测回由式(3)两式相减求得［6～8］:

式中，消去了大地高差的影响，△h即为两台天线之间的相位中心垂直偏差之差。实验方案设置两个对照组:第一组为两台相同的 Trimble R7 GNSS，使用Trimble Zephyr Model 2天线;第二组为一台Trimble R7 GNSS和一台Trimble R8 GNSS，R8使用Model 3天线。两组间隔观测，上午和下午各观测一个测回，连续观测3 d，实验结果取绝对值见表1和表2。

第一组实验结果表1

第二组实验结果表2

单独看表1或表2，测值之间的波动并不大，特别是上午和下午的观测量取平均后波动幅度均在1 mm之内，可以认为参与检测的仪器的相位中心垂直偏差相对稳定。表1中，最大的互差值为2.6 mm，在实际高程测量中可以作为偶然误差处理。两表对比看，第二组使用不同仪器时互差明显大于第一组使用相同仪器，但R7和R8均为Trimble公司生产的仪器，因此差别不大。对比实验结果进一步说明在GPS高程测量中尽量选择相同的天线，若条件不允许，则可以选用同厂家生产的近似型号的天线。

4 天线相位中心偏差垂直分量改正方法

GPS高程传递时需要消除相位中心垂直偏差的影响，作者提出了以下的方法改正这项误差。选择长江某大桥建设工地江边6个跨河高程控制点作为实验场地，测量点均为强制观测墩。其中KJ1和KJ2为主跨河高程传递点，其余4点为高程拟合基准点。实验仪器为两台Trimble R7 GNSS和两台Trimble R8 GNSS。根据第2节的实验结果，在GPS跨河高程测量实验方案中取表1的均值1.7 mm作为R7之间的高差改正值，同样取表2的均值4.55 mm作为R7和R8之间的高差改正值，具体改正方法分为数据采集和数据处理两个步骤:

(1)数据采集时，至少需要一个测点进行全时段观测，可以和网中所有测点形成基线。如图4中，在KJ1和KJ2两测点架设两台R7进行全时段观测，总计观测两个时段，第一时段在A1和A3上架设R8，第二时段在A2和A4上架设R8。记录每个测点上的仪器型号，确定各条基线两端采用的仪器，即确定各条基线的高差改正值。

(2)数据处理时，首先选择一个全时段观测的点作为起算点进行自由网平差。如图4中，在KJ1和KJ2中选择一个点作为起算，平差后得到未改正的大地高。其次以起算点为中心，在各条基线另一端点的大地高中减去本基线的高差改正值，得到改正后的大地高。

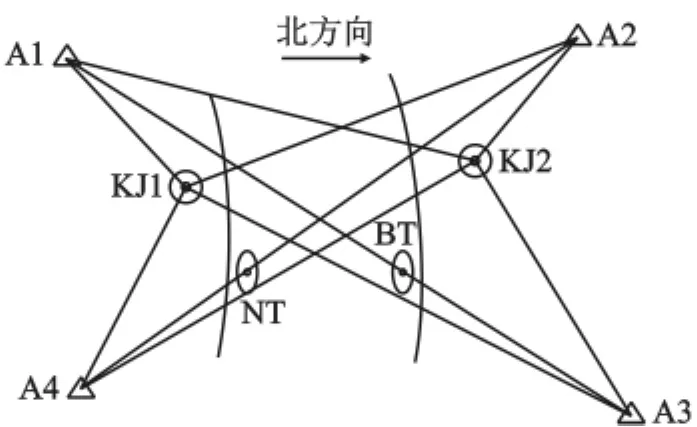
图4 实验场地基线示意图

GPS高程传递最终需要通过高程异常拟合将GPS大地高系统转为施工中使用的正常高系统。本文根据已建立好的高程异常模型，利用未改正的大地高和改正后的大地高分别拟合KJ1和KJ2，结果对比如下:

拟合正常高对比表3

5 结论

数据后处理得到的改正后的大地高中各测点相位中心垂直偏差与起算点近似相等。虽然并没有完全消除各测点的绝对相位中心垂直偏差，但是将GPS网中各点相位中心垂直偏差统一为一个近似值，这个值对高程拟合的影响相对一致，可以认为垂直偏差是高程异常的一部分。通过表3的数据对比可以看出本方法对于提高GPS高程传递精度有明显作用，具备一定实用价值。本改正方法存在一定局限性:

(1)需要进行相位中心垂直偏差检验，较为耗时，仪器种类不宜多。

(2)数据采集时需要额外记录详细信息，工作量较大，网中测点不宜多。

(3)改正大地高时无法实现全自动化，效率较低，网中基线不宜多。

GPS跨河高程传递测区范围不大，可以采用小网观测，网中测点相较少，因此可以满足数据采集时的要求。本改正方法只针对GPS小网的高精度高程传递对于常规的GPS大网高程传递或平面控制并不适用。

［1］范建军，王飞雪.GPS接收机天线相位中心变化对基线解的影响［J］.宇航学报，2007，28(2):298～304.

［2］高玉平.GPS接收机天线相位中心偏差的检测［J］.陕西天文台台刊，2001，24(1):121 ～126.

［3］高伟，晏磊，徐绍铨等.GPS天线相位中心偏差对GPS高程的影响及改正研究［J］.仪器仪表学报，2007，28(11):2052～2058.

［4］陈逸群，刘大杰.GPS接收机天线相位中心偏差的一种检定与计算方法［J］.测绘通报，2000(12):15～16.

［5］王婷婷，朱瀚，陈义.利用完全旋转法检测GPS接收机天线相位中心三维偏差［J］.测绘通报，2008(11):14～17.

［6］孔祥旗，李冠男.GPS天线相位中心的确定及其消除偏差方法［J］.科技信息，2008(4):52～52，94.

［7］姜晨光，张莉娜，吕振勇.GPS接收天线相位中心稳定性及高程零位检测方法的新探索［J］.测绘标准化，2001.17(3):11～14.

［8］翟清斌，齐维君.GPS天线相位中心变化及测试［J］.测绘科学，2004，29(2):60 ～63.