变电站水平双分裂导线的短路张力分析
2012-09-22张谢平
张谢平
(华东电力设计院,上海市,200001)
0 引言
为了消除电晕、提高载流能力,变电站内的220和500kV导线多采用水平双分裂形式。当同相导线中有短路电流通过时,2根次导线之间的电磁吸引力使导线发生变形,从而产生一个附加的弹性拉力,该拉力通常称为分裂导线的“第一最大张力”[1-4]。
第一最大张力对导线、绝缘子、架构以及电气设备端子有很大的影响[5-7]。目前设计人员多使用文献[1]提出的方法来计算第一最大张力,即以相邻间隔棒之间的一段导线作为研究对象,根据短路前后导线形状和长度的差异来推导出附加张力值。文献[1]提出的方法虽然简单,但却存在较大的计算误差,在初始张力较小的情况下误差更大。
文献[2]也提出了计算第一最大张力的方法,推导了短路时绝缘子串的位移和构架的弹性变形,较文献[1]的方法有所改善。但该方法只适用于悬挂点等高、无引下线的简单情形,未对导线的整体状态做出描述。
本文将以整跨导线作为研究对象,推导短路情况下导线的状态方程,通过求解状态方程得出短路时的导线张力以及变形量。与文献[1]的计算方法相比,本文的研究对象为导线的整体而非局部,并且对绝缘子串、引下线等都进行了分析,经实例计算证明所提出的方法更为合理。
1 未发生短路时软导线的状态方程
根据文献[1],软导线状态方程为

式中:H为软导线水平张力;S为导线截面积;αx为导线温度系数;θ为导线温度;E为导线弹性模量;γ为不等高悬挂时的倾斜角度;D为各段导线荷载因数之和,D=∑ΔD,m和n对应2种不同的导线状态。
软导线的形状如图1所示。若已知状态n的张力,则求解式(1)便可求得状态m对应的张力。
2 发生短路时软导线的状态方程
当双分裂导线中流过短路电流时,由于2根次导线的相互吸引作用,导线的长度和水平张力都会发生变化,此时仍可用式(1)对导线进行求解。

图1 不等高悬挂的软导线Fig.1 Flexible conductor with two ends suspended at different height
2.1 次导线受力分析
当2根次导线中流过相同的电流时,由于电磁力的作用,2根导线会相互吸引,从而使导线发生形变,如图2所示。
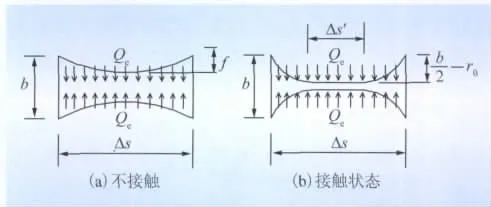
图2 短路时次导线受力变形示意Fig.2 Schematic diagram of sub-conductor’s deformation during short-circuit
图2 中,b为分裂间距;Δs为间隔棒间距;Qe为2根间隔棒之间的电磁吸力;r0为次导线半径;Δs'为接触状态时的接触长度。
根据电磁场定律[8],电磁力可有如下的近似表示:
(1)导线不接触时为

(2)导线接触时为

式中I为单根导线中通过的短路电流周期分量有效值。
根据力矩平衡条件,电磁力和导线水平张力之间有如下关系:
(1)导线不接触时为

(2)导线接触时为

由式(2)~(5)可得
(1)导线不接触时为

(2)导线接触时为
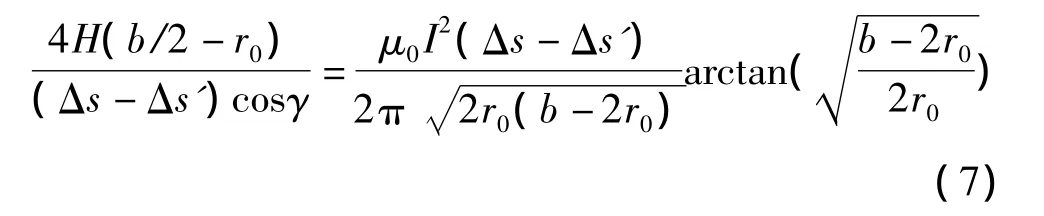
2.2 发生短路时导线的长度
根据图2所示,软导线的长度可表示为[1,9]

式中:si为各段分裂导线(相邻两间隔棒之间)由短路引起的长度增量。
(1)导线不接触时为

(2)导线接触时为

2.3 发生短路时导线的状态方程
由于短路不会改变导线垂直方向的受力,因此短路前后荷载因素亦无变化。在式(1)的基础上,推导出导线状态方程[1,10]:
(1)导线不接触时为

(2)导线接触时为
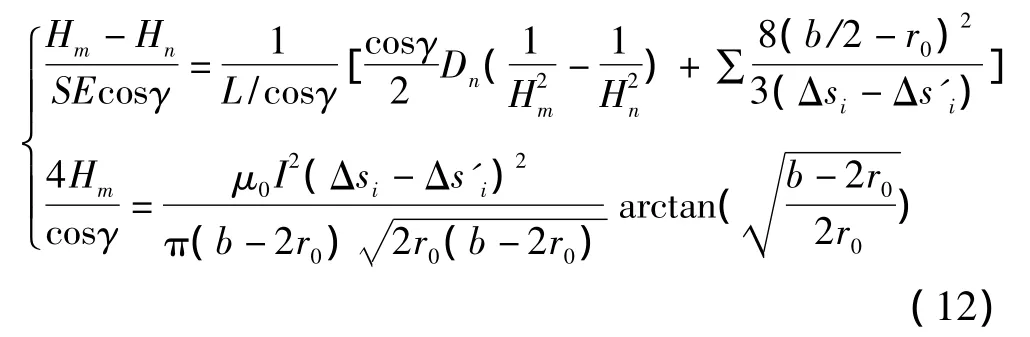
发生短路时,状态方程中除了增加水平张力H外,又增加了变量fi(不接触状态)或变量Δs'i(接触状态),同时增加了方程的个数。通常一跨导线中的间隔棒均匀放置,因此各小段分裂导线的变形相同。
3 计算实例
算例1:变电站内的500kV设备连线采用水平双分裂软导线,设备间无高差。导线跨距为8m,分裂间距为400 mm,间隔棒每隔1m布置1副。导线型号为2×LGJQT-1400,间隔棒型号为MRJ-1400-400,短路前导线弧垂为0.8m,短路电流为63 kA。用文献[1]和本文的方法分别进行了计算,计算结果见表1。

表12 种计算方法结果(算例1)Tab.1 Comparison between two methods(example 1)
算例2:变电站内采用水平双分裂跨线,长度为50m,绝缘子串为1×31×XWP-100的耐张串和可调串,导线型号为 2×LGKK-600,分裂间距为400 mm,间隔棒型号为MRJ-600K-400,每隔10m设置1副。导线等高悬挂,短路前弧垂为3m,短路电流为63 kA。用文献[1]和本文的方法分别进行了计算,结果见表2。

表2 2种计算方法结果比较(算例2)Tab.2 Comparison between two methods(example 2)
由表1、2可见,由于初始张力较小,2种计算方法的结果相差很大,其中短路张力相差近10倍。因此用文献[1]的方法计算此类工况时误差太大,不宜采用。对于较长的跨线,由于初始张力较大,2种方法计算所得的短路张力相差不大,但导线的接触长度有较大差别。
2种方法之所以有如此大差异,是因为文献[1]将相邻间隔棒之间的一段导线作为研究对象,通过比较短路前和短路时该段导线的变形及受力情况,来计算出短路时的导线张力。该方法虽然简单,但却忽视了导线的整体状态:短路时在电磁力的作用下,不仅2根次导线的间距发生变化,整跨导线的弧垂、张力、长度也随之改变,只有将整跨导线作为研究对象才会得出较精确的结果。
4 结语
本文推导了短路情况下水平双分裂导线的状态方程,可用于求解短路时的导线状态和张力。
此状态方程虽然为非线性方程组,但通常间隔棒在1跨导线中为均匀放置,因此方程组中除了水平张力外只增加了1个未知数,可以采用迭代法来求解。
[1]水利电力部西北电力设计院.电力工程电气设计手册1[M].北京:中国电力出版社,2006:379-383.
[2]蓝增珏,叶景星.500kV变电所电气部分设计及运行(上册)[M].北京:水利电力出版社,1987:181-187.
[3]石改萍.超高压配电装置分裂导线次档距长度的选择[J].山西电力,2007(增刊):40-42.
[4]张士利.220kV线路相分裂导线吸引、扭绞分析[J].山西电力,2004(1):4-6.
[5]DL/T 5222—2005导体和电器选择设计技术规定[S].北京:中国电力出版社,2005.
[6]DL/T 5218—2005 220~500kV变电所设计技术规定[S].北京:中国电力出版社,2005.
[7]范锡普.发电厂电气部分[M].北京:中国电力出版社,1995:120-105.
[8]冯慈璋.电磁场[M].2版.北京:高等教育出版社,1983.
[9]能源部东北电力设计院.电力工程高压送电线路设计手册[M].北京:水利电力出版社,1989:196-201.
[10]顾惠琳.工程力学[M].上海:同济大学出版社,2004.
