基于边界探测的InSAR最小二乘整周相位解缠方法

陈 强，杨莹辉，刘国祥，程海琴，刘伟堂

西南交通大学遥感信息工程系，四川成都610031

基于边界探测的InSAR最小二乘整周相位解缠方法

陈 强，杨莹辉，刘国祥，程海琴，刘伟堂

西南交通大学遥感信息工程系，四川成都610031

Abstract：An improved method of phase unwrapping is proposed based on unwrapping edge detection．The unwrapping edge is predicted and propelled by comparing the optimal solutions and suboptimal solution in least squares method．The integer ambiguity of unwrapped phase is extracted through increasing phase increment into wrapped phase．The feasibility and accuracy of proposed method is tested and validated by using simulated data and ERS－1／2 InSAR interferogram covering Hong Kong and Shenzhen area．The testing results show that the proposed method can correctly extract 99．5%phase values from the simulated interferogram with strong noise．The accuracy of phase unwrapping tested on the InSAR interferogram reaches±0．12rad．

Key words：edge detection；integer ambiguity；phase unwrapping；least squares method；InSAR

为解决最小二乘相位解缠方法一直存在收敛性差和非整周性相位解算问题，提出基于解缠边界探测并搜索整周相位值的解缠方法，采用最小二乘次优解与最优解的阈值判别准则，预测解缠趋势并逐步推进相位解缠边界，并在解缠迭代计算中附加相位搜索增量以提取相位整周值。试验分别基于噪声干扰的模拟图和香港、深圳地区的ERS－1／2卫星SAR影像干涉图，采用边界探测算法进行相位解缠计算，试验结果表明，本文解缠方法对附加强噪声的模拟干涉图能正确解缠出99．5%的相位值，真实SAR影像干涉图的解缠精度达到±0．12rad。

边界探测；相位整周数；相位解缠；最小二乘方法；InSAR

1 引 言

合成孔径雷达干涉测量（interferometric synthetic aperture radar，InSAR）凭借其独特的地面分辨率高、覆盖范围广、基于面观测等技术特点，在应用于数字高程模型（digital elevation model，DEM）的生成、地表形变的监测等方面已表现出巨大的潜力［1－3］，InSAR正逐渐发展为一种重要的空间对地观测新技术。

InSAR技术是通过处理和分析覆盖同一地区的两幅或多幅SAR影像，从多个信号混叠的干涉相位数据中，分离和提取出与地形起伏、地表形变相关的信号分量，从而解算出地面高程或地表位移信息［4－7］。InSAR数据处理主要包括影像配准、重采样、相位干涉、参考相位的去除、相位解缠和地理编码等，每个处理环节的精细程度对于InSAR最终测量成果的精度和可靠性都具有极其重要的影响。

相位解缠是InSAR数据处理中的一个关键环节，也一直是SAR干涉处理中的难点和重点。相位解缠是将干涉相位中丢失的相位整周数采用几何解析或数值分析的方法恢复出其相对整周值，从而完成地形相对高差的解算或形变的检测［8－9］。相位解缠的准确性将直接影响到InSAR生成数字高程模型或地表形变检测的精度。在InSAR相位解缠中，如果相邻像素的相位差满足连续的条件，即相邻像素相位差绝对值小于π，则相位解缠很容易正确完成。然而，在真实的SAR影像干涉图中，造成相邻相位不连续、相位周跳的因素较多，如雷达阴影、失相关噪声、影像配准等因素引起相位数据不连续，这给相位解缠工作带来极大的困难，InSAR相位解缠仍然是一个十分棘手的问题。

目前相位解缠算法较多，主要归结为基于路径控制的积分法和基于最小二乘的整体求解法［10－13］。积分法的思路是计算像素行向和列向的一阶相位差分，然后对一阶差分连续积分即可求得解缠相位。由于干涉相位图存在奇异点，积分路径应受到约束以避免局部噪声相位误差的传播，这种算法的关键是按一定的原则对奇异点定位并予以连接作为积分路径的“防火墙”，即积分时不能穿越这些路径。最小二乘算法的思想是解缠后的相位梯度与缠绕相位梯度差异平方和为最小意义下的整体求解，使用带权估计方法可削弱奇异相位对解缠结果的影响。除此两种主要方法外，基于网络流的相位解缠算法、遗传算法、神经网络法等，国内外也有过相应的理论研究与应用尝试［14－19］。

对于干涉图残差点较少的区域，采用基于路径控制的积分法可以得到较为可靠的结果，而对于残差点较多的干涉图，如大多数非Tandem模式、有一定时间间隔的SAR影像对，由于很难正确设置路径控制线（或枝切线），积分方法很难得到可靠的解缠结果，而最小二乘法则通过使缠绕相位梯度与真实相位梯度之差的平方和为最小来实现相位解缠，它对于残差点较多的区域仍能有效解缠，但其明显不足之处是，相位解缠的同时将误差扩散到了非噪声区域，且解缠相位与缠绕相位之差不是整周值，解缠相位不能满足一致性条件。

本文在传统最小二乘相位解缠算法基础上，提出了一种基于边界推进收敛加速的最小二乘整周相位解缠（phase unwrapping based on least squares with integer ambiguity，Publesia）方法，它通过对干涉图解缠边界的逐步推进和解缠相位的整数化迭代计算，较好地解决了最小二乘收敛性慢和整周值的求解问题。

2 最小二乘解缠原理

最小二乘相位解缠是基于解缠相位梯度与缠绕相位梯度之差的平方和为最小的准则来实现相位解缠，它是数学意义上全局范数最小的求解问题［10－12］，其目标函数可表示为

由于最小二乘相位解缠的目标是使缠绕相位与解缠相位梯度差的平方和为最小，已有研究表明，这种最小二乘法相位解缠可以归结为求解下式离散泊松方程的过程［13］

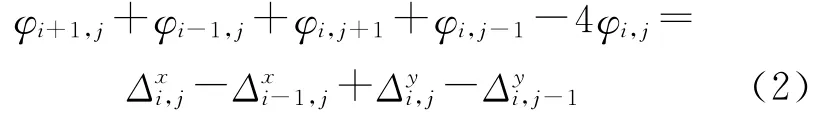
令

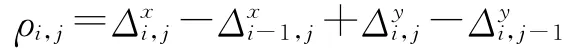
则有

该泊松方程满足如下条件方程

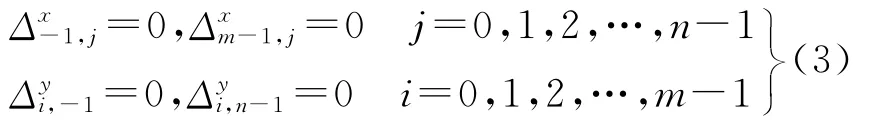
式中各符号含义与式（1）相同。上述方程为无加权的最小二乘解法，其缺点在于解缠过程中它穿过残差点区域而并非绕过它们进行解缠，这可借助为相位数据引入权重值来加以克服，即加权的最小二乘相位解缠算法。对于那些因噪声或其他因素跳变的相位，可以将其权重赋为0，使它们不影响全局解缠过程。如果以InSAR中的相位质量图或者相干系数图作为相位数据的权重ωi，j，则有0≤ωi，j≤1，那么无加权的最小二乘就转化为加权的最小二乘算法，其改进的加权方程式如下［10－12］

按照上述的传统最小二乘算法，经过多次高斯赛德尔迭代所求得的最小二乘解具有很好的连续性和平滑性，但该解在任意一点的结果可能有噪声误差扩散，并且解缠相位与缠绕相位的差不是整周值，解缠相位数据不能很好地满足一致性条件。此外，该方法还存在迭代收敛较慢且在某些区域不收敛的问题，算法的收敛性有待提高。

3 边界推进式相位解缠算法

根据最小二乘方法在迭代过程中逐步趋近于最优解的思想，笔者提出探测解缠边界的推进式解缠算法，将解缠区域划分为已解缠区域和待解缠区域，对解缠区域的边界逐步分析判断，对每次迭代计算的解缠相位值附加相位增量以正确提取整周相位值，通过逐步推进解缠边界，完成全局相位的一致性解缠处理。具体计算方法如下。

传统最小二乘算法每次计算返回的相位值可由下式计算得到［10－12］式中表示像元（i，j）在第n次迭代计算后的解缠相位值。将同一像元两次迭代的解缠相位之差定义为Δ＝φni，j－φn－1i，j，根据Δ的具体数值判断解缠的趋势，设置一个较小的判别阈值TC，阈值大小的有效性应充分顾及迭代计算的稳定性与时间效率的平衡。然后采用如下关系式对本次解缠的φni，j进行计算

式中，dφ是为加快迭代收敛速度而设置的一个相位增量值，其值的大小根据试验结果获得，使解缠相位能更快地趋近于最优值。将前一次迭代计算的结果作为次优解，则本次计算得到的作为最优解，再对解算结果进行如下的相位整周计算。

式中第1项Int为提取解缠相位整周值的函数。上述整周解缠计算能逐步正确解算出每个像素点的缠绕相位整周值，确保全局解缠相位的一致性。

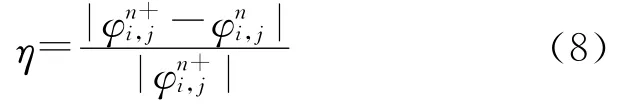
基于上述流程，在每次迭代结束后还需进行边界条件的判断，以此判别已解缠相位和未解缠区域，采用如下判别式式中表示第n次迭代计算出的解缠相位值；表示在第n次迭代的基础上再按式（5）进行计算所得的新相位值。设Tη为解缠判断阈值，若η＞Tη，则判断该像素未解缠，反之则认为已解缠。按此方法可探查已解缠与未解缠的边界像素，并将其进行标记。判断解缠边界后，由于仍无法直接判定边界两侧的已解缠和未解缠区域，但可判定边界上的点仍未得以解缠，然后将边界点的相位值都加上一个相位增量δ。则对于η＞Tη，有

式中，Δ为同一像元两次迭代解缠相位之差；相位增量δ的绝对大小可取小于π的一个固定相位数值，其有效性应充分顾及迭代计算的稳定性与时间效率的平衡。

依据上述计算流程，经过少量次数的迭代即可将解缠边界上的像素点逐一相位解缠，解缠边界不断向前推进，直至最终解缠边界像素数为零，迭代终止，完成全局相位解缠。整个算法的基本流程如图1所示。

图1 Publesia算法流程图Fig．1 Flow chart of Publesia method

需要提及的是，在本算法中考虑了相邻两次迭代相位差与附加相位增量对相位解缠的加速过程，使得算法的时间效率相当高，并且解缠迭代计算中的整数化过程保证了解缠相位的一致性和整周值的正确求解，较好地解决了传统最小二乘算法非整周性解算和收敛速度较慢的问题。

4 仿真数据分析

为验证本文相位解缠算法的可行性和可靠性，笔者基于MATLAB语言工具开发了Publesia相位解缠程序，并使用模拟数据和真实InSAR干涉图对所开发的算法和程序进行验证。

模拟干涉图的主要干涉参数为：基线水平角α＝0°，有效基线长度B⊥＝150m，干涉相位的模糊度高为59m，雷达波长5．7cm，影像区域大小为100像素×100像素，区域内高程分布为0～200m，干涉图中分布有20%区域的低相干区域（复相关系数≤0．2）。

该模拟区域的地形绝对相位如图2所示，相位分布范围为0～30rad，在上述干涉参数条件下得到的缠绕干涉图如图3。干涉图的四角边界区域视为完全失相干区域，通过设置其权值为零以避免这些像素点对全局相位的解缠干扰。采用本文前述的最小二乘整周相位解缠算法（Publesia）对干涉图（图3）进行相位解缠，并设置相位差阈值TC＝π／10，相位增量dφ＝π／6。迭代计算至第4次、6次、8次、10次、12次和14次得到的解缠相位图如图4（a）～（f）。

图2 模拟地形绝对相位图 图3 模拟干涉相位图Fig．2 Simulated topographic Fig．3 Simulated phase interferogram

图4 边界逐次推进的相位解缠过程Fig．4 The process of phase unwrapping by Publesia

从图4中的（a）～（f）可以看出，随着迭代次数的逐次增加（4～14次），相位解缠的边界正如前述算法中所描述的过程，逐步向前推进，当迭代计算进行到第14次时，解缠相位图与原真实相位图完全一致，正确解缠率达到100%，验证了该算法的正确性。

然后使用含有噪声干扰的仿真数据来验证算法的可行性与可靠性。对上述图3的干涉相位图分别施加弱噪声和强噪声干扰，噪声方差分别为0．27rad和0．73rad，采用本文的Publesia方法对弱噪声干涉图和强噪声干涉图分别进行相位解缠。在弱噪声条件下（噪声方差为0．27rad），解缠结果与真实相位仍然保持高度一致性，正确解缠率能达到100%。在强噪声条件下（噪声方差为0．73rad），逐次迭代计算得到的干涉相位图如图5所示，（a）～（f）分别表示迭代第4次、6次、8次、10次、12次和15次的计算结果。

图5 附加强噪声的相位解缠图Fig．5 Unwrapped phase from noisy interferogram by Publesia

为定量评估相位解缠结果的可靠性及解缠精度，笔者对解缠结果（第15次迭代计算）相位值进行数据统计，将解缠相位与原真实相位值进行差异比较，并进行精度评定。相位差异ΔΦ的统计数据如表1所示，并采用如下公式计算解缠相位的均方根误差（RMSE）式中，mφ为解缠相位的均方根误差；φunwrapped为采用本文方法解缠所得到的相位值；φtruth为相位真值。

表1 解缠相位精度统计表Tab．1 Accuracy assessment of unwrapped phase

从表1中的统计数据与精度评估可以看出，采用本文Publesia方法进行强噪声干涉图相位解缠，全图中约占99．5%的像素其解缠相位值与真实相位值的绝对差异小于0．1rad，仅占约0．5%的像素其解缠相位值与相位真值差异超过0．1rad，表明本文解缠算法对于强噪声（0．73rad）干涉图仍然能够实现正确解缠，解缠精度达到±0．005rad。

5 InSAR干涉图解缠试验

在采用模拟干涉图验证了算法的可行性和可靠性之后，笔者进一步使用欧洲空间局（ESA）的ERS－1／2卫星在香港和深圳地区获取的两幅单视复数影像（SLC）开展雷达干涉试验，SAR影像的局部覆盖范围如图6所示。这两幅影像获取时间分别为1996－03－18（主影像）和1996－03－19（从影像），该干涉影像对的有效空间基线长度为98．6m，模糊度高约为103．9m，采用DORIS软件进行干涉数据处理［20］，得到图6中方框区域的干涉相位条纹图，如图7所示。

图6 SAR影像振幅图Fig．6 Amplitude map of SAR image

图7 InSAR干涉相位图Fig．7 InSAR interferogram derived from DORIS

采用本文解缠算法对图7的干涉相位开展相位解缠，经迭代计算后得到的解缠相位如图8所示。为评价本文解缠算法对该真实干涉图相位解缠的精度与可靠性，进行了解缠结果的外符合精度检查，采用斯坦福大学的Curtis W．Chen所开发的Snaphu解缠程序对图7的干涉图开展相位计算。Snaphu方法充分考虑相位解缠的地形信息与形变提取物理意义，基于极大验后估计费用函数，利用统计特性寻找全局优化解，Snaphu方法对不同类型数据解缠均具有较高的可靠性［14，21］。因此，当难以获得解缠真值时，选用Snaphu计算结果作为本文解缠算法结果的评判依据，将本文Publesia计算结果与Snaphu解缠图进行差异比较，相位差异统计数据如图9所示。

图8 解缠相位图Fig．8 Unwrapped phase by Publesia

图9中，横轴表示解缠相位差异区间（单位：rad），按相位差异区间统计，在（－1．0，1．0）内统计单元长度为0．1rad，在差异值超过该区间后，将（－∞，－1．0］内的像素统一归算到－1．0rad处，［1．0，＋∞）区间内像素统一归算到1．0rad处，纵轴为像素个数的百分比。从图9中的统计数据可以看出，采用本文Publesia方法对ERS－1／2 SAR干涉图进行相位解缠，图中有93%像素的解缠相位与Snaphu方法解缠相位的绝对差异小于0．5rad，以Snaphu方法解缠相位作为参考，计算两种方法相位解缠的均方根误差（RMSE），得到解缠精度为±0．12rad。为进一步验证本文方法的解缠精度，采用加权的最小二乘解缠方法对图7进行了相位解缠计算，解缠结果与本文方法计算结果的均方根差（RMSE）达到±0．28rad，表明本文方法与Snaphu方法的解缠结果具有较高的一致性，而加权最小二乘解缠方法的计算结果偏差相对较大。

图9 解缠相位差异统计Fig．9 The statistics of unwrapped phase difference

此外也需提及的是，图9中Publesia方法与Snaphu方法的解缠结果也存在相位差超过0．5rad的少量像素，产生这种差异的原因主要来源于解缠方法的差异，Snaphu方法是基于统计费用流的非线性优化约束算法，而本文方法是在全局优化基础上顾及了整周模糊度参数的一致性解算，有效避免了相位质量差的像元引起的全局误差传播，本文方法对于强噪声干涉图相位解缠具有较好的稳健性。

此外，对于解缠时间效率的比较，将Publesia方法、Snaphu方法和加权的最小二乘解缠方法，分别在相同的计算环境下予以测试，Snaphu方法对图7干涉图相位解缠所耗时间为5．0s，本文Publesia方法所耗时间为5．7s，而加权最小二乘算法所耗时间大于30s，这表明本文Publesia方法与Snaphu方法解缠效率相当，而相对于加权最小二乘方法，解缠效率有明显提高。

6 结 论

本文针对InSAR最小二乘相位解缠方法存在的收敛性差和整周模糊度解算的问题，提出了将干涉图逐步划分为未解缠区域和已解缠区域，对迭代计算的解缠相位值附加相位增量以正确提取整周相位值，通过逐步探测解缠边界以此推进相位解缠过程，最终完成全局干涉相位的一致性解缠处理。

基于所开发的Publesia相位解缠方法，对模拟干涉图和ERS－1／2卫星SAR干涉图分别开展相位解缠试验，在施加强噪声干扰的模拟干涉图中相位解缠的正确率达到99．5%，解缠的均方根误差为±0．005rad，试验结果验证了本文解缠方法的可行性和可靠性。在ERS－1／2卫星SAR影像覆盖香港和深圳地区的干涉图相位解缠试验中，有93%的相位解缠数值与Snaphu方法解缠结果保持较高的一致性，且本文方法对于强噪声干涉图相位解缠具有较好的稳健性，解缠效率得以显著改善。

［1］ MASSONNET D，ROSSI M，CARMONA C，et al．The Displacement Field of the Landers Earthquake Mapped by Radar Interferometry［J］，Nature，1993，364：138－142．

［2］ LIU Guoxiang，DING Xiaoli，CHEN Yongqi，et al．Ground Settlement of Chek Lap Kok Airport Hong Kong，Detected by Satellite Synthetic Aperture Radar Interferometry［J］．Chinese Science Bulletin，2001，46（21）：1778－1782．

［3］ LIU Guoxiang，DING Xiaoli，LI Zhilin，et al．Experimental Investigation on DEM Generation through InSAR［J］．Acta Geodaetica et Cartographica Sinica，2001，30（4）：336－342．（刘国祥，丁晓利，李志林，等．使用InSAR建立DEM的试验研究［J］．测绘学报，2001，30（4）：336－342．）

［4］ SHAN Xinjian，ZHANG Guohong．An Analysis of Dynamic Evolution of Preseismic Interferometric Deformation Fields in Seismic Area［J］．Seismology and geology，2006，28（3）：441－446．（单新建，张国宏．孕震区震前D－InSAR干涉形变场动态演化图像分析［J］．地震地质，2006，28（3）：441－446．）

［5］ ZHANG Qin，ZHAO Chaoying，DING Xiaoli，et al．Research on Recent Characteristics of Spatio－temporal Evolution and Mechanism of Xi＇an Land Subsidence and Ground Fissure by Using GPS and InSAR Techniques［J］．Chinese Journal of Geophysics，2009，52（5）：1214－1222．（张勤，赵超英，丁晓利，等．利用GPS与InSAR研究西安现今地面沉降与地裂缝时空演化特征［J］．地球物理学报，2009，52（5）：1214－1222．）

［6］ WANG Yan，LIAO Mingsheng，LI Deren，et al．Subsidence Velocity Retrieval from Long－term Coherent Targets in Radar Interferometric Stacks［J］．Chinese Journal of Geophysics，2007，50（2）：598－604．（王艳，廖明生，李德仁，等．利用长时间序列相干目标获取地面沉降场［J］．地球物理学报，2007，50（2）：598－604．）

［7］ CHEN Qiang，DING Xiaoli，LIU Guoxiang，et al．Baseline Recognition and Parameter Estimation of Persistent－scatterer Network in Radar Interferometry［J］．Chinese Journal of Geophysics，2009，52（9）：2229－2236．（陈强，丁晓利，刘国祥，等．雷达干涉PS网络的基线识别与解算方法［J］．地球物理学报，2009，52（9）：2229－2236．）

［8］ GHIGLIA D C，PRITT M D．Two－dimensional Phase Unwrapping：Theory，Algorithms，and Software［M］．New York：Wiley，1998．

［9］ GOLDSTEIN R M，ZEBKER H A，WERNER C L．Satellite Radar Interferometry：Two－dimensional Phase Unwrapping［J］．Radio Science，1988，23（4）：713－720．

［10］ ZEBKER H A，LU Y P．Phase Unwrapping Algorithms for Radar Interferometry：Residue－cut，Least－squares，and Synthesis Algorithms［J］．Journal of the Optical Society of America A，1997，15（3）：586－598．

［11］ YUE Huanyin，GUO Huadong，HAN Chunming，et al．Phase Unwrapping of Noisy SAR Interferograms［J］．Acta Geodaetica et Cartographica Sinica，2002，31（2）：151－156．（岳焕印，郭华东，韩春明，等．噪声条件下的干涉SAR相位解缠［J］．测绘学报，2002，31（2）：151－156．）

［12］ XU Caijun，WANG Hua．Comparison of InSAR Phase Unwrapping Algorithms and Error Analysis［J］．Geomatics and Information Science of Wuhan University，2004，29（1）：67－71．（许才军，王华．InSAR相位解缠算法比较及误差分析［J］．武汉大学学报：信息科学版，2004，29（1）：67－71．）

［13］ XIANG Maosheng，LI Shukai．InSAR Phase Unwrapping Using Poisson’s Equation with Dirichlet Boundary Conditions［J］．Acta Geodaetica et Cartographica Sinica，1998，27（3）：204－210．（向茂生，李树楷．用狄氏边界的泊松方程进行InSAR相位解缠的研究［J］．测绘学报，1998，27（3）：204－210．）

［14］ CHEN C W，ZEBKER H A．Two－dimensional Phase Unwrapping with Use of Statistical Models for Cost Functions in Nonlinear Optimization［J］．Journal of the Optical Society of America A，2001，18（2）：338－351．

［15］ YU Yong，WANG Chao，ZHANG Hong，et al．A Phase Unwrapping Method Based on Network Flow Algorithm in Irregular Network［J］．Journal of Remote Sensing，2003，7（6）：472－477．（于勇，王超，张红，等．基于不规则网络下网络流算法的相位解缠方法［J］．遥感学报，2003，7（6）：472－477．）

［16］ COSTANTINI M．A Novel Phase Unwrapping Method Based on Network Programming［J］．IEEE Transactions on Geoscience and Remote Sensing，1998，36：813－831．

［17］ LIU Zilong，CAI Bin，DONG Zhen．A New InSAR Phase Unwrapping Method Based on Local Frequency Estimationand Multigrid Technique［J］．Acta Geodaetica et Cartographica Sinica，2010，39（1）：82－87．（刘子龙，蔡斌，董臻．基于局部频率和多网格技术的InSAR相位解缠算法［J］．测绘学报，2010，39（1）：82－87．）

［18］ PRITT M D，SHIPMAN J S．Least－squares Two－dimensional Phase Unwrapping Using FFT＇s［J］．IEEE Transactions on Geoscience and Remote Sensing，1994，32（3）：706－708．

［19］ CARBALLO G F，FIEGUTH PW．Probabilistic Cost Functions for Network Flow Phase Unwrapping［J］．IEEE Transactions on Geoscience and Remote Sensing，2000，38（5）：2192－2201．

［20］ KAMPES B M，HANSSEN R F，PERSKI Z．Radar Interferometry with Public Domain Tools［C］．Proceedings of FRINGE 2003Workshop．Frascati：［s．n．］，2003．

［21］ CHEN C W，ZEBKER H A．Phase Unwrapping for Large SAR Interferograms：Statistical Segmentation and Generalized Network Models［J］．IEEE Transactions on Geoscience and Remote Sensing，2002，40（8）：1709－1719．

（责任编辑：雷秀丽）

InSAR Phase Unwrapping Using Least Squares Method with Integer Ambiguity Resolution and Edge Detection

CHEN Qiang，YANG Yinghui，LIU Guoxiang，CHENG Haiqin，LIU Weitang
Department of Remote Sensing and Information Engineering，Southwest Jiaotong University，Chengdu 610031，China

P237

A

1001－1595（2012）03－0441－08

国家自然科学基金（41072220；41074005）；中央高校基本科研业务费专项资金（SWJTU09CX010；SWJTU11ZT13）

2011－03－24

修回日期：2011－10－14

陈强（1974—），男，博士，副教授，主要从事摄影测量与遥感的教学和科研工作。

First author：CHEN Qiang（1974—），male，PhD，associate professor，majors in photogrammetry and remote sensing．

E－mail：swjtucq＠sina．com