基于RBF的指标规范化的水安全评价模型

臧 蕾, 李祚泳

（成都信息工程学院,四川成都 610225）

0 引言

水安全包括水资源及由此而引发的经济安全、社会安全甚至上升到国家安全高度的问题。因此,水安全问题越来越成为全世界关注的焦点。国内外对水安全定性研究较多,而在系统性和量化方面显得不足[1]。当前常用的水安全评价主要有层次分析法、模糊分析法、物元分析法、集对分析法、属性识别法等不确定性分析评价方法[2-6]。这些方法虽然能反映水安全评价过程中具有的模糊性、灰色性、不相容性和既确定又不确定的特征,但是评价过程中需要构造众多的评价函数,工作量大,而且这些评价函数的设计无规律可循,主观性较大。因此,实际使用不简便。BP网络、支持向量机及投影寻踪等智能评价模型指标较多时有大量参数需要优化确定[7],编程计算较复杂。环境质量评价实际上是根据一定的判别标准对环境质量的模式的好坏做出评价与区分,是典型的模式识别问题[8]。人工神经网络在模式识别方面表现出了较好的特性,尤其是最近几年提出和开始研究的径向基函数（Radial Basis Function,RBF）人工神经网络较为有效地解决了以上问题,在环境质量评价中得到应用。径向基神经网络的分类能力、学习效率及泛化能力都优于BP网络,而且隐节点数容易确定,需要优化的权值亦较少。RBF神经网络不仅具有良好的推广能力,而且避免了向反向传播那样烦琐、冗长的计算,克服了计算时容易陷入局部极小值的问题,学习速度也是传统BP网络无法比拟的。不过,传统的径向基函数网络模型的隐层节点基函数的中心矢量的各指标分量值不相同,因而基函数对各指标不具有普适性。论文提出基于径向基函数的指标规范化的水安全评价模型（Normalized Value Radial BasisFunction,NV-RBF）,模型的隐层节点基函数中心矢量的同级标准各指标分量规范值相同,这个标准规范值可取为所有指标规范值的平均值,因而具有普适性。将模型应用于山东省水安全实例评价,得到相应区域3个方案的水安全评价结果与其他方法的评价结果基本一致。

1 基于径向基函数网络的指标规范值表示的水安全评价模型

1.1 水安全指标体系的建立及指标参照值和指标值的规范变换式

选取山东省水安全评价作范例,其23项指标及5级分级标准如表1所示。虽然表1中不同指标同级标值差异很大,有的甚至相差几个数量级。但若能分别对各指标设定一个适当的参照值cj0和相应于参照值cj0的指标值的规范变换式（1）和式（2）。各指标参照值cj0和指标值的规范变换式（1）和式（2）的设定原则为:通过对各项指标各级标准值之间的变化规律（比如线性或非线性）的观察、比较、分析和归纳,使23项不同指标的同级标准值cjk经式（1）和式（2）变换后的规范值 x′jk差异尽可能小,而不同级标准之间的标准规范值差异尽可能大。这一过程需要对选择的cj0和规范变换式反复设置、试算和调整,直到满意为止。从而可以认为所有各指标皆“等效”于某个规范指标。23项水安全指标的参照值cj0见表1。

式中:x′j为指标j的规范变换值,cj为指标j的实际值或标准值,cj0为指标 j的参照值。

表1 水安全评价指标参照值、分级标准值及山东省水安全评价3个可行方案

1.2 基于指标规范值的径向基函数网络模型的基本思想

设径向基函数网络（Radial Basis Function,RBF）模型的学习样本为指标规范值构成的 m维规范矢量x′i=（x′i1,…,x′ij,…,x′im）。因此,网络输入节点数为 m;输出节点数可取 l=1;隐层节点数与分级标准数相同。通常选取如式（3）所示的高斯函数φk作为每个隐节点k处的径向基函数。

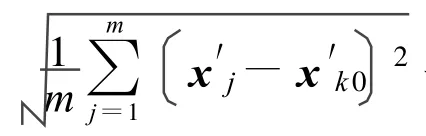
式中,φk为式（3）表示的高斯径向基函数,wk为第k个隐节点与输出节点的连接权值。

表2 NV-RBF网络中各基函数“恒定”中心矢量分量值 x′k0、方差σ2k、优化后的连接权值wk及网络期望输出值yk0、实际输出值yk及分级区间（a,b]

1.3 可调参数的优化

式（4）中基函数的方差σ2k和连接权值wk需要优化确定。经分析和运行调试,隐层5个节点的基函数的方差σ2k均设定为0.05,如表2所示。因而需要优化确定的参数只是权值wk（k=1,2,3,4,5）。为此,需要设计如式（5）所示的优化目标函数式:

式中,K=5,为分级标准数目;yk为由式（4）计算得到的第k级标准样本的NV-RBF网络实际输出值;yk0为第k级标准样本的NV-RBF网络期望输出值。yk0为设定的与具体指标数无关,而只与k级标准有关的网络期望输出目标值。各级标准样本的网络期望输出值yk0的设定原则为:限制yk0∈[0,1],开始各级标准样本的网络期望输出值yk0可在[0,1]区间内等距取值,随着优化的进行,亦需反复调整相邻两级标准样本的网络期望输出值之间的间距,最终满足优化目标函数式（5）极小为止。设定水安全的NV-RBF网络的各级标准样本期望输出值yk0亦见表2。设定 wk∈[-2,2],在满足优化目标函数式（5）条件下,用猴王遗传算法对式（4）中的连接权值wk反复迭代优化。猴王遗传优化算法的参数设置如表3所示。有关猴王遗传算法的基本思想和算法实现详见文献[9]。当目标函数式min Q=2.59×10-4时,停止迭代,得到优化后的wk,如表2所示。从而得到对式（4）优化后适用于任意m（1≤m≤23）项指标的水安全评价的NV-RBF网络模型输出表达式:

式中,φi（i=1,2,3,4,5）用式（3）表示。

将水安全各级标准样本的23项指标规范值构成的矢量x′k代入式（3）和式（6）中,计算得到水安全各级标准样本的NV-RBF网络实际输出值yk,及分级标准的划分区间,见表2。

表3 猴王遗传算法的参数设置

2 实例分析

山东省水安全评价可供选择的3个方案的指标数据见表1。分别将表1中的3个方案各指标值用式（1）、式（2）规范变换后的规范值,代入式（3）和式（6）中计算,并根据表2输出值的划分区间做出评价结果见表4。

表4 山东省3个方案的水安全评价结果

NV-RBF网络模型对山东省水安全评价的结果与TS-SVM模型[10]、属性识别法[11]的评价级别基本一致。比较文献[12]的结果可以看出:山东省目前水安全状况隶属等级为3级,即属于“安全”级别。根据计算结果:若实施方案1和方案2,山东省水安全状况会有较明显改善,将隶属于“基本安全”级别3级;而方案3对水安全状况的改善较小。

3 结束语

对于表1中的任意m（1≤m≤23）项指标的水安全评价,不用编程,也不需设计评价函数,只需用式（1）和式（2）计算得到的各指标规范值代入式（3）和（6）计算。因而NV-RBF模型与其他方法相比,计算简单,使用方便,为水安全评价提供了一种新方法。

对表1中的23项指标以外的其他指标,只要能适当设定这些指标的参照值cj0及相应的指标值的规范变换式,使计算出的这些指标的各级标准规范值在表1中的23项指标的同级标准规范值范围内,则优化得出的式（3）和式（6）仍可作为基于RBF网络的这些指标的水质评价模型,而不会有太大的偏离影响,因而优化得出的NVRBF水安全评价模型具有较广泛意义的普适性和通用性。

[1] 阮本清,魏传江.首都圈水资源安全保障体系建设[M].北京:科学出版社,2004:50-52.

[2] 樊彦芳,刘凌,陈星,等.层次分析法在水环境安全综合评价中的应用[J].河海大学学报:自然科学版,2004,32（5）:512-514.

[3] 安鑫,周维博,马艳,等.基于熵权的模糊综合评价法在水安全中的应用[J].水资源研究,2011,32（1）:18-19,46.

[4] 陈志军,朱健.艾比湖流域水安全的多指标物元综合评价[J].水资源研究,2010,31（4）:13-15.

[5] 何焰,由文辉,吴健.上海市水环境生态安全评价[J].水资源保护,2006,22（6）:18-20,27.

[6] WANG Wen-sheng,JIN Ju-liang,DING Jing,et al.A new approach to water resources system assessment:set pair analysis method[J].Science in China Series E:Technological Sciences,2009,32（10）:3004-3016.

[7] Kuo Yiming,Liu Chenwang,Lin Kaohuang.Evaluation of the ability of an artificial neural network model to assess the variation of groundwater quality in an area of blackfoot disease in Taiwan[J].Water Research,2004,38（1）:148-158.

[8] 李宗伟,辛沂,王美娟.径向基网络在环境质量评价中的应用[J].临沂师范学院学报,2001,23（6）:12-14.

[9] 郭晨海,谢俊,刘军,等.连续非线性规划的猴王遗传算法[J].江苏大学学报:自然科版,2002,23（4）:87-90.

[10] 汪嘉杨,王文圣,李祚泳,等.基于 TS-SVM 模型的水安全评价[J].水资源保护,2010,26（2）:1-4,9.

[11] 张龙云,曹升乐,杨尚阳.属性识别理论在水安全评价中的应用研究[J].山东大学学报:工学版,2006,36（5）:70-72.

[12] 田守岗,曹升乐.山东省水安全评价体系及对策研究研究报告[R].济南:山东省水利科学研究院,2006.