基于二阶泛模型的无模型自适应控制及参数整定

王晶，纪超，曹柳林，靳其兵

(北京化工大学 信息科学与技术学院，北京，100029)

无模型自适应控制器将不依赖被控对象具体数学模型的“泛模型”和某些“控制功能”模块相结合[1-2]，采用边建模边控制的方式，得到新的观测数据后，再建模再控制，使每次得到的“泛模型”逐渐精确，从而控制器的性能也随之得到改善。无模型自适应控制作为一种不依赖于对象数学模型的简单、有效、具有广泛适用性的先进控制策略，在很多复杂过程控制中得到成功应用[3]。但是对于相同的控制系统而言，不同的控制器参数所得到的控制效果完全不同。特别是当工况发生改变时，对象特性将发生一些变化，当前控制器参数可能造成响应曲线的振荡，导致生产事故的发生[4]。同时，当代社会对节能减排的要求也越来越高，而较好的控制效果可以达到节能减排的目的。要获得较好的控制效果，就需要较好的控制器参数。因此，优化控制器参数是非常必要的。本文作者首先针对MFAC中的关键因素“泛模型”进行改进，由一阶扩展为二阶“泛模型”，使得每次迭代得到的“泛模型”更加精确，从而大大提高控制精度。然后针对现阶段无模型自适应控制领域中参数整定问题研究较少的现状，提出适用于改进无模型自适应控制的基于下降梯度法的参数优化整定算法，并运用不同的性能指标进行控制器参数整定和结果对比分析研究。

1 基于二阶泛模型的改进无模型自适应控制器设计

1.1 二阶“泛模型”

对于一般离散时间非线性系统：

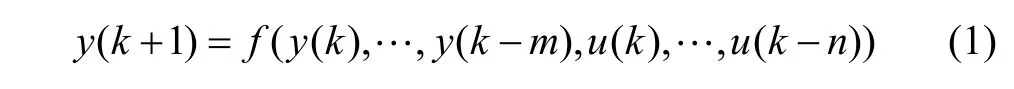
其中：y(k)和u(k)分别为系统的输出与输入；m和n分别为系统阶数[5]。

首先假设：

假设1：系统(1)是输入输出可观测的，可控制的。即：对某一系统一致有界的期望输出信号 y*( k+ 1)，存在一致有界的可行控制输入信号，使得系统在此控制输入信号的驱动下其输出等于系统的期望输出。

假设2：f (…)关于系统当前的控制输入信号u(k)的偏导数是连续的。

假设3：系统(1)是广义Lipsehitz的，即满足对任意时刻的k和 Δu(k )≠0有：

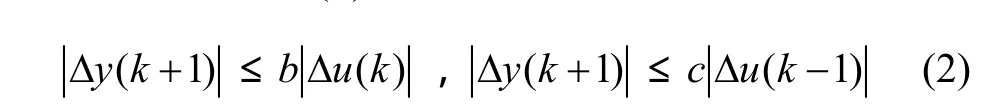
其中：Δ y(k +1)=y(k+1) -y(k )；Δu(k)=u(k)-u(k -1)；b是1个大于0的常数。

对非线性系统(1)，如果满足以上假设条件，那么当 Δu(k )≠0和 Δu(k - 1)≠0时，一定存在伪偏导数φ1(k )和φ2(k )，使得系统可以用下式表示[6]：

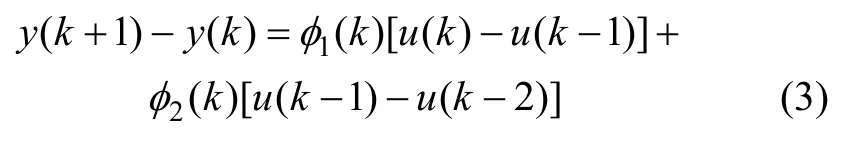
简写为：

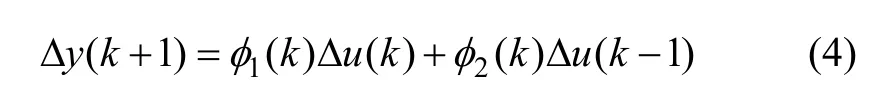
称式(3)为系统(1)的二阶“泛模型”(Second-order universal model)。众所周知，系统当前时刻的输出不仅与当前时刻的输入有关，而且与以前时刻的输入相关，因此，上述二阶泛模型的提出可以代表更广泛的系统信息。

1.2 基于二阶“泛模型”无模型自适应控制规律

1.2.1 控制规律导出

考虑如下的控制输入准则函数：

其中：λ是权重因子； y*( k+ 1)是k+1时刻的给定值。λ[u (k)-u(k-1)]2的引入，使得控制输入量的变化受到约束，且能克服稳态跟踪误差。将式(3)代入式(5)，并对u(k)求导，令其为0，得：

根据下降梯度法，得：

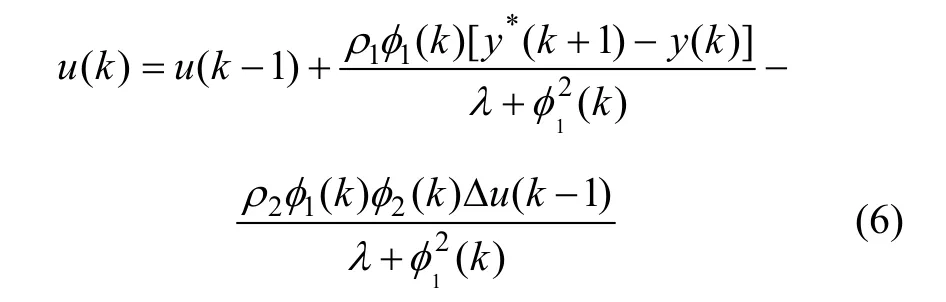
其中：ρk(0＜ρk≤2)是步长序列[6]。

从控制律算法(6)可以看出：此类控制系统与受控系统参数数学模型结构、系统阶数无关，仅用系统I/O数据设计[7]。

1.2.2 伪偏导数估计

传统的参数估计准则函数应该是极小化系统模型输出与系统真实输出之差的平方，然而，应用此类准则函数推导出的参数估计算法在估计参数时，其参数的估计值经常变化太快，或者就是对某些突变的个别不准的干扰过于敏感，为此，提出如下新的参数估计准则函数：

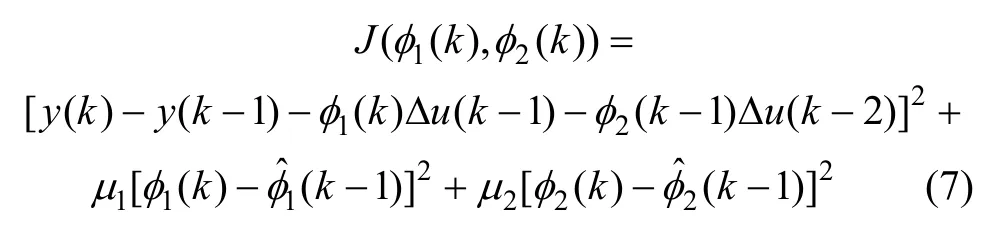
其中：y(k)为k时刻系统的输出；μ1和μ2为权重因子。分别对 φ1(k )和φ2(k )求导并令其等于 0，得到偏伪导数估计：

其中：1η和2η为步长序列。

2 二阶“泛模型”无模型控制器参数整定

针对无模型自适应控制器参数较多、不易得到合适参数的特点，必须对其进行控制器参数整定。首先，二阶“泛模型”无模型自适应控制器的可调参数为1ρ，2ρ，λ，1η，2η，1μ和2μ。经过工程实践与大量仿真实验发现：λ，1η，2η，1μ和2μ对控制器影响很小，因此，参数整定的重点在于1ρ和2ρ。而2ρ又是在二阶“泛模型”概念提出后才出现，根据式(6)可知：其在(0, 2)之间取定后，只要与1ρ的比值一定，对系统的影响并不明显。因此，对于整个二阶“泛模型”无模型控制器参数整定的核心在于1ρ的优化。

参数优化算法需要根据离线数据对被控对象辨识出一个简单的模型，该模型只是被控对象的近似，在此对任何高阶复杂对象均使用二阶加纯滞后模型近似，由于参数整定效果并未因辨识误差较大而变差，因此此时的系统辨识并不违反无模型控制的宗旨。即假设所有对象经系统辨识均近似为二阶惯性纯滞后对象，

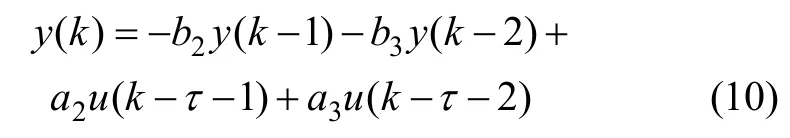
式中：τ为纯滞后时间。

传统的参数优化算法比较简单[8]，基本原理较容易理解，使用起来比较方便，计算量不大。但对于比较复杂的被控对象，传统整定方法难以使用。因此，需要选择一种优化精度高且可以适用于较为复杂的被控对象的参数优化算法，而梯度下降法可以很好地满足以上要求。

2.1 性能指标的选取

二阶“泛模型”无模型自适应控制器的参数优化就是寻找合适的控制器参数，即使在工况发生变化的时候，系统仍具有较小的超调量，较快的响应速度和较高的控制精度。根据性能要求不同，参数优化时所采用的目标函数也大不相同。

2.1.1 ISE系列目标函数

最优 PID控制器参数整定算法由 Zhuang等[9]提出，其最优准则为：

式中：e(θ,t)为进入控制器的误差信号；θ为控制器参数构成的集合。在最优准则中考虑了3个n的取值，即n=0，1，2。当n=0时，为误差平方(ISE)准则；当n=1时，为时间加权的误差平方积分(ISTE)准则；当n=2时，为时间平方加权的误差平方积分(ISTTE)准则[10]。

下面针对n=0时，采用梯度下降参数优化算法进行推导。

首先，将性能指标(11)转化成离散形式，即：

最终根据式(6)、(10)和(12)联立，得到基于 ISE性能指标的梯度下降法参数优化算法：

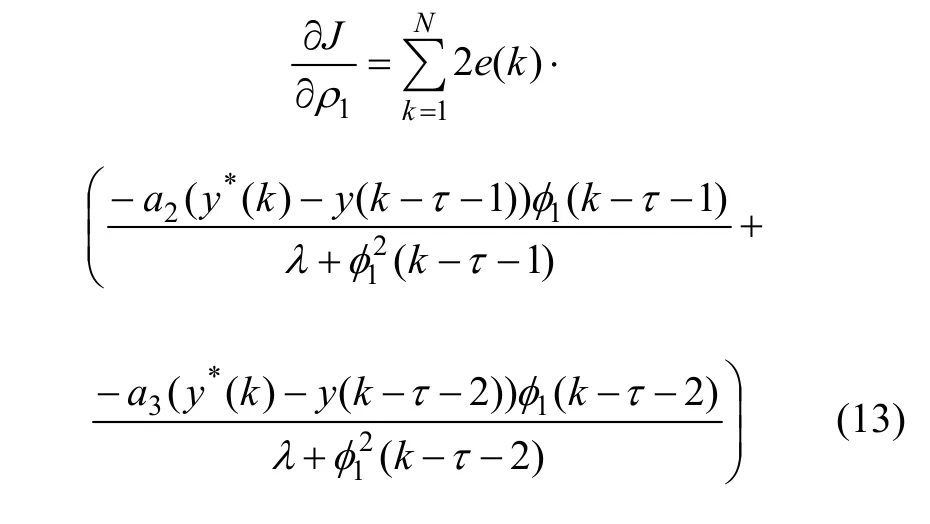
2.1.2 IAE系列目标函数

经常使用的还有误差绝对值积分(IAE)以及误差绝对值与时间乘积的积分(ITAE)最小为目标的调节规律[11]，其表达式分别如式(14)和式(15)所示：

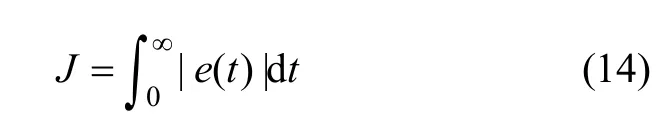
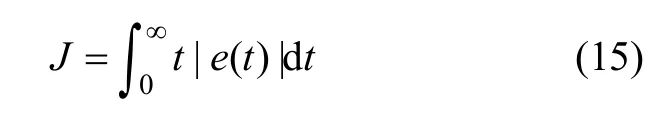
类似于ISE性能指标优化算法的推导过程，可以得到基于IAE性能指标的梯度下降法参数优化算法：

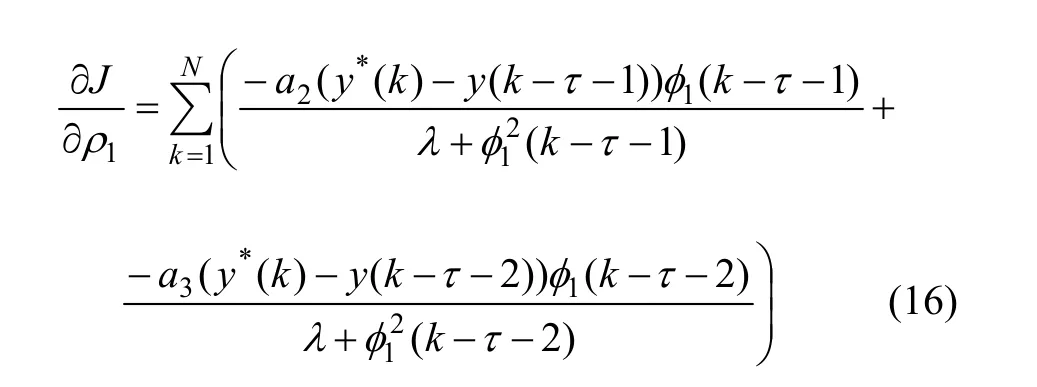
2.1.3 Jeu目标函数

上述各准则考虑了综合性能指标，包括响应速度、稳定性和超调量这些指标。它使用起来比较方便，但是如果控制器对某一性能指标的要求较高，例如：要求最大超调量最小、峰值时间最短、上升时间最短等，上述表达式难以实现。因此，提出了组合目标函数[12]。

为了获得满意的过渡性能和动态特性，采用误差平方积分性能指标作为参数优化的目标函数。同时为了避免超调量过大，在目标函数中加入了控制器输出的平方项。目标函数为：

式中：e(t)为系统误差；u(t)为控制器的输出；1ω和2ω为权值。其参数优化算法为：

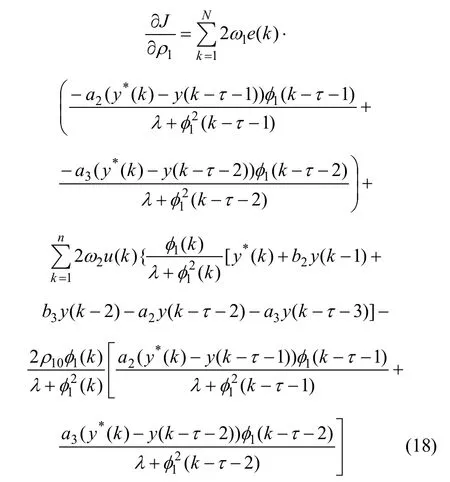
另外，也可以在性能指标(17)的基础上加入对超调量δ、上升时间tr等约束条件，即：

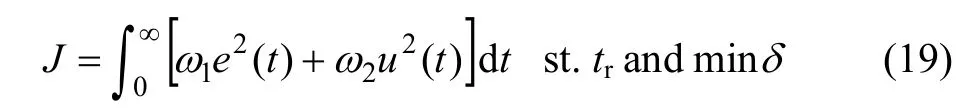
2.2 改进无模型控制的参数整定算法实现

运用梯度下降法对二阶“泛模型”无模型自适应控制器的参数整定思路如下：

(1) 根据离线数据对被控对象辨识出 1个简单的模型；

(2) 根据控制要求，选取参数优化的性能指标；

(3) 将其余无需参数整定的控制器参数进行设定；

(4) 根据式(6)可知1ρ的选取范围为(0, 2)，因此，在参数整定时，在该范围内选择初始值；

(5) 根据性能指标的计算结果得到∂J∂1ρ；

(6) 运用下降梯度法对1ρ进行调整，即

(7) 判断是否满足性能指标要求，若满足，则参数整定结束；若没达到要求，则跳转到第 5步继续整定。

上述(5)～(7)步为运用梯度下降法进行二阶“泛模型”无模型控制参数优化的步骤，如图1所示。

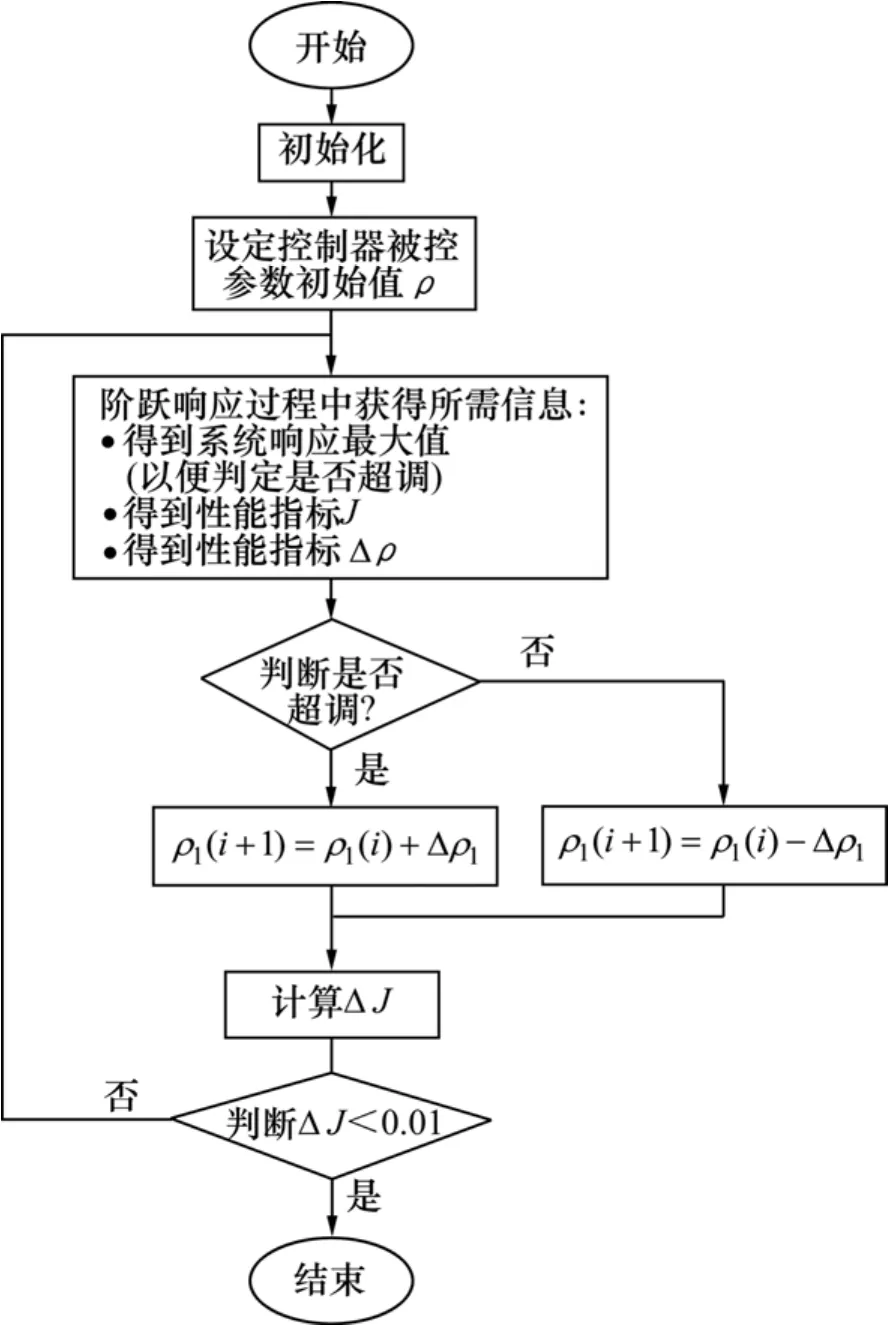
图1 梯度下降法参数优化流程图Fig.1 Flow chart of parameter optimization of gradient descent method

3 仿真研究

针对三容水箱的三阶惯性纯滞后对象为[13]：

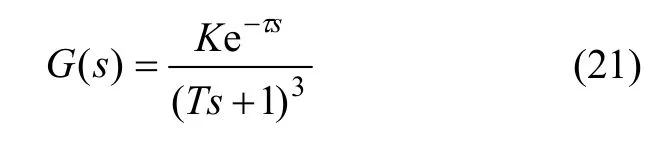
其中：静态增益K=5；惯性时间常数T=3；纯滞后时间τ=60。

3.1 二阶“泛模型”无模型自适应控制仿真研究

从式(6)可以看出：2ρ的作用是减弱无模型自适应控制器的控制作用，使得控制器输出更加稳定与准确。

仿真参数为：

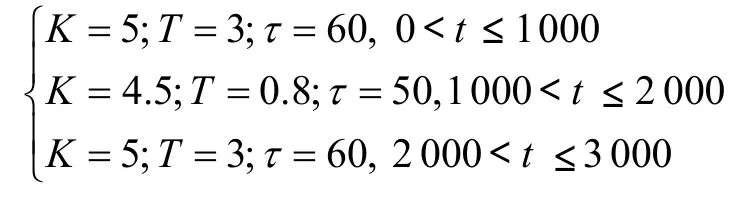
改进无模型自适应控制器控制参数为：

ρ1=0.003 5；ρ2=0.35；λ=2；μ=2；ε=0.1；

MFAC控制参数ρ=0.002 8(其余参数同二阶“泛模型”无模型自适应控制器)。相对于ρ1来说，ρ2的数量级较大。因为从式(6)可知： y*(k+1) -y(k )＞＞Δu(k -1)。二阶“泛模型”无模型自适应控制器与MFAC控制方法的系统响应曲线对比如图2所示。

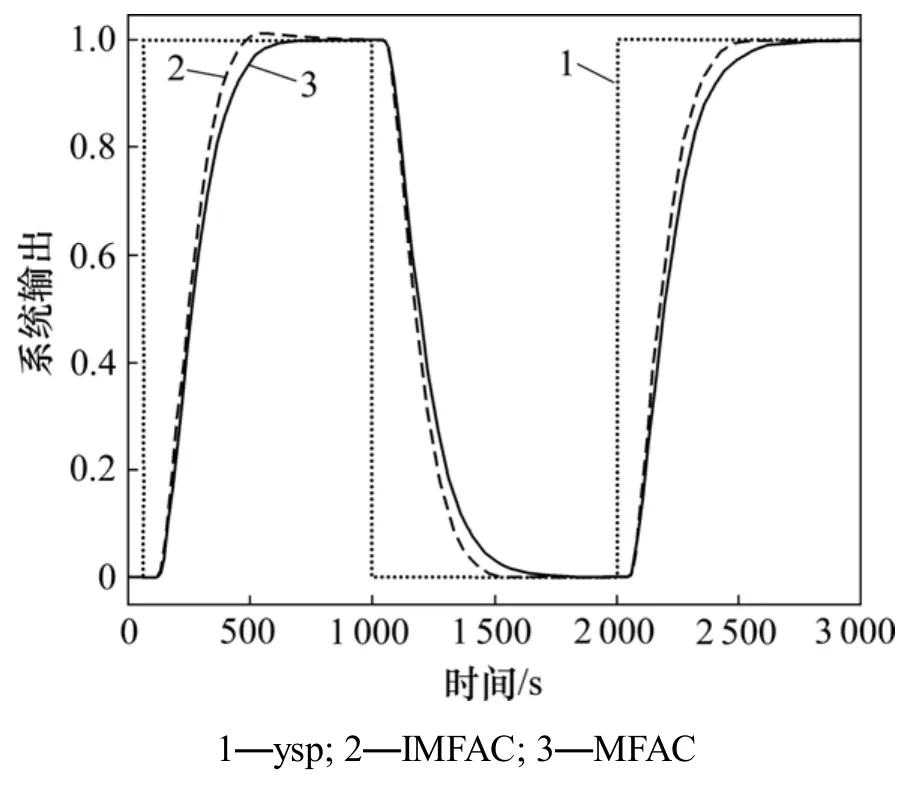
图2 改进MFAC与常规MFAC响应曲线对比Fig.2 Comparison of improved MFAC and MFAC

由图2可知：二阶“泛模型”无模型自适应控制算法与MFAC的调节时间分别为326 s和523 s；超调量分别为1.40%和0.14%；而上升时间分别为216 s和300 s。可以看出：在2种控制方法中，二阶“泛模型”无模型自适应控制器的调节时间最短，相比MFAC快近200 s，尽管超调量比MFAC的略大，但满足控制系统设计要求(2%)，上升时间也较快，并且在1 000 s时，当被控对象特性发生了改变时，二阶“泛模型”无模型自适应控制算法依旧最先到达新稳态值，并且无超调，因此，二阶“泛模型”无模型自适应控制具有较好的鲁棒性和较快的响应速度。

3.2 二阶“泛模型”无模型自适应控制参数优化的仿真研究

参数优化算法需要根据离线数据对被控对象辨识出一个简单的模型，如图3所示，可以看出实际对象与辨识出的近似对象相差很大。实际对象与辨识对象对比如下。

根据辨识结果可以看出：辨识出的被控对象参数与实际对象偏差很大，这就说明在二阶“泛模型”无模型控制器的参数整定中辨识对象不需要较高的精度，并且运用简单的二阶纯滞后对象即可对所有高阶被控对象近似，适用范围广。接下来根据辨识出的对象带入参数优化算法对实际三阶纯滞后对象进行控制器参数优化。

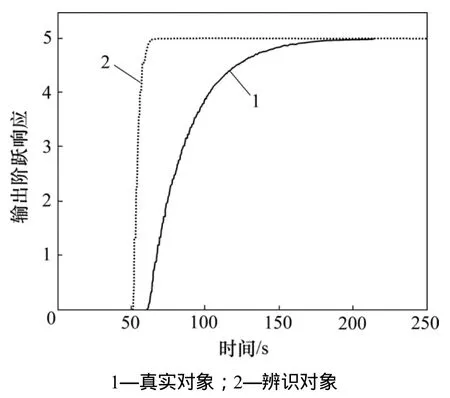
图3 实际对象与辨识对象的阶跃响应曲线Fig.3 Step response for real and identified objective

3.2.1 ISE系列目标函数参数优化仿真

运用下降梯度法为优化算法，并以式(11)为目标函数对二阶“泛模型”无模型自适应控制器进行参数优化，优化结果如图4所示，分析结果如表1所示。

当n=0时着重权衡大的误差，在初始值1ρ=0.01时，控制系统具有较短的上升时间，但超调较大，在实际系统中往往存在偏差小但波动次数多，调节时间长，系统稳定裕量偏小等缺点；当n为1和2时较少考虑大的起始误差，着重权衡过渡过程后期出现的误差，有较好的选择性，反映系统的快速性和精确性，相比较而言，ISTE的优化效果最好。

3.2.2 IAE系列目标函数参数优化仿真

运用目标函数式(14)和(15)对二阶“泛模型”无模型自适应控制器进行参数优化，优化控制效果如图 5所示，优化迭代次数及最终参数结果如表2所示。

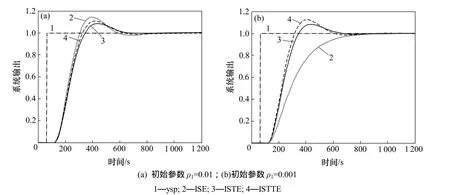
图4 目标函数分别为ISE，ISTE和ISTTE的参数优化效果Fig.4 Comparison of ISE, ISTE and ISTTE parameter optimization effects

表1 ISE系列目标函数参数优化效果对比Table 1 Results of ISE, ISTE and ISTTE parameter optimization

表2 IAE系列目标函数参数优化效果对比Table 2 Results of IAE and ITAE parameter optimization

IAE所具有的性质与式(11)的相同，ITAE与其有较大不同。从图5可以看出：当初始参数1ρ=0.01时，两者的优化效果并没有明显差异，但当初始值为1ρ=0.001时，ITAE优化出的参数明显比IAE的好。ITAE对刚开始的误差要求比较低，而对响应曲线最后出现的误差要求比较高。它体现了控制系统所要求的快速性和精确性的品质。因此，它经常在优化或整定过程中得到应用。

3.2.3 对比总结

将上述各种目标函数中优化效果最好的几种性能指标进行对比，以便得到最佳目标函数。

首先，通过对下降梯度法参数优化的仿真可以看出：在辨识模型与实际模型相差较大的情况下，仍可以将二阶“泛模型”无模型自适应控制器参数调整到较好的程度，证明本优化算法可以只运用二阶纯滞后模型，便可以优化任何高阶复杂的真实对象，具有较强的实用性。

由图6及表3可以看出：ISTE目标函数主要对较大的误差求和。以此为目标函数整定出来控制参数的响应曲线，具有快速的上升速度，需要较短的上升时间。但是，超调量比较大，稳定所需要的时间比较长，往往经过多次较小的偏差波动才能稳定。因此，不能很好满足控制的要求。

而ITAE目标函数相对于ISTE来说，优化效果相对较好，稳定性更好一些。但是，相比于带约束条件的Jeu，稳定性与快速性都差。这里在Jeu性能指标的基础上增加了约束条件：超调量δ小于1%；上升时间tr＜300 s，即如式(19)所示。此类Jeu-tr型指标对应的优化迭代次数最少，更加实用与快速。因此，为了满足综合控制性能的要求，选择Jeu-tr作为目标函数对无模型自适应控制器进行参数优化能得到最好的结果。

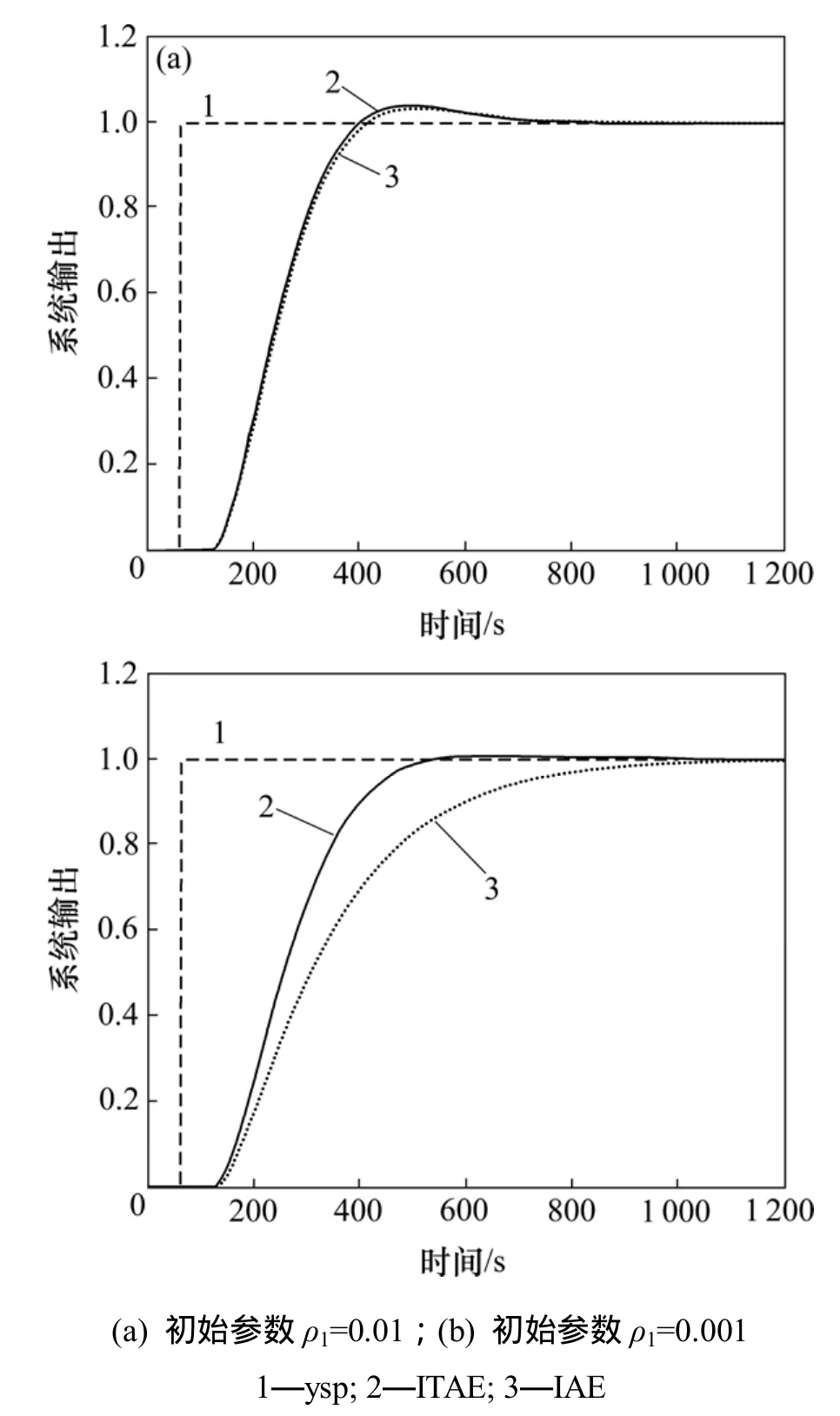
图5 目标函数分别为IAE和ITAE的参数优化效果Fig.5 Comparison of IAE and ITAE parameter optimization effects

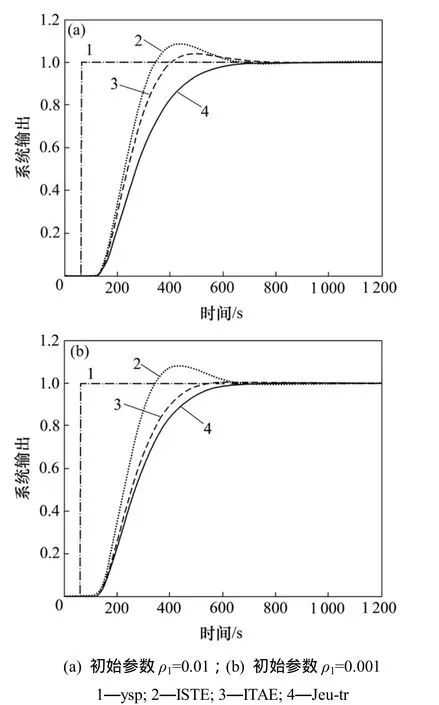
图6 目标函数分别为ISTE，Jeu-tr和ITAE的参数优化效果Fig.6 Comparison of ISTE, Jeu-tr and ITAE parameter optimization effects

表3 目标函数参数优化效果对比Table 3 Results of ISTE, Jeu-tr and ITAE parameter optimization

4 结论

(1) 本文基于无模型自适应控制中“泛模型”的概念，从提高控制过程中“泛模型”精度的角度出发，提出了二阶“泛模型”概念，给出了基于二阶“泛模型”的无模型自适应控制(Second order universal MFAC)算法，并推导了控制器和泛模型的迭代求解方程。与常规无模型自适应控制比较的仿真结果表明，该方法具有较快的响应速度，并且对过程对象参数的摄动具有较强的鲁棒性。

(2) 为了解决改进无模型自适应控制器参数整定问题，提出了下降梯度参数优化算法，针对不同类型的目标函数进行参数优化。仿真结果说明了该参数优化算法的有效性；采用带约束条件的误差平方与控制器输出平方加权(Jeu)为目标得到的参数控制效果最佳，适宜二阶“泛模型”MFAC的参数整定。

[1] 韩志刚. 无模型控制器理论与应用的进展[J]. 自动化技术与应用, 2004, 23(2): 34-37.HAN Zhi-gang. The progress of theory and application of model free controller[J]. Techniques of Automation and Applications,2004, 23(2): 34-37.

[2] Hou Z S, Huang W H. The model-free learning adaptive control of a class of SISO nonlinear systems[C]//Proceedings of the American Control Conference. New Mexico, l997: 343-344.

[3] Tan K K, Lim S Y, Lee T H, et al. Adaptive predictive control of a class of SISO nonlinear systems[J]. Dynamics and Control,2001, 1l(2): 151-174.

[4] 李文博. 锅炉控制系统设计及其在PCS7上的实现[D]. 北京:北京化工大学信息科学与技术学院, 2010: 23-24.LI Wen-bo. Design of control system of boiler and realization based on PCS7[D]. Beijing: Beijing University of Chemical Technology. College of Information Science and Technology,2010: 23-24.

[5] 马彦, 陈雪, 解小华, 等. 带有单输出跟踪微分器的无模型自适应控制[J]. 仪器仪表学报, 2009, 30(6): 204-208.MA Yan, CHEN Xue, XIE Xiao-hua, et al. Research on MFA control algorithm with tracking differentiator[J]. Chinese Journal of Scientific Instrument, 2009, 30(6): 204-208.

[6] 侯忠生. 非参数模型及其自适应控制理论[M]. 北京: 科学出版杜, 1999: 117-163.HOU Zhong-sheng. Non-parameter model and adaptive control theory[M]. Beijing: Science Press, 1999: 117-163.

[7] Cheng G S. Model-free adaptive control[J]. IEEE Computing and Engineering, 2004, 1(3): 28-33.

[8] 周宝林, 朱建跃, 蔡宁生, 等. 过程控制系统中PID控制器参数优化的研究[J]. 能源技术, 2001, 22(5): 194-197.ZHOU Bao-lin, ZHU Jian-yue, CAI Ning-sheng, et al. A study on parameter optimization of PID controller in process control system[J]. Energy Technology, 2001, 22(5): 194-197.

[9] Zhuang M, Atherton D P. Automatic tuning of optimum PID controllers[J]. Control Theory and Applications, IEE Proceedings D, 1993, 140(6): 216-224.

[10] Zhuang M, Atherton D P. Tuning PID controllers with integral performance criteria[C]//International Conference on CONTROL & Institution of Electrical Engineers Computing and Control Division. Proceedings of IEE Conference on Control.London: IEE, 1991: 481-486.

[11] 徐峰, 李东海, 薛亚丽. 基于ITAE指标的PID参数整定方法比较研究[J]. 中国电机工程学报, 2003, 23(8): 206-210.XU Feng, LI Dong-hai, XUE Ya-li. Comparing and optimum seeking of PID tuning methods base on ITAE index[J].Proceedings of the CSEE, 2003, 23(8): 206-210.

[12] 熊伟丽, 徐保国, 周其明. 基于改进粒子群算法的PID参数优化方法研究[J]. 计算机工程, 2005, 31(24): 41-43.XIONG Wei-li, XU Bao-guo, ZHOU Qi-ming. Study on optimization of PID parameter based on improved PSO[J].Computer Engineering, 2005, 31(24): 41-43.

[13] 金尚泰, 侯忠生. 一类非线性大滞后系统的改进无模型自适应控制[J]. 控制理论与应用, 2008, 25(4): 623-626.JIN Shan-tai, HOU Zhong-sheng. An improved model-free adaptive control for a class of nonlinear large-lag systems[J].Control Theory & Applications, 2008, 25(4): 623-626.