一类无穷时滞积分微分方程周期解的稳定性
2012-09-20常啸
常 啸
(安徽财经大学统计与应用数学学院,安徽蚌埠233030)
0 引言
泛函微分方程是20世纪70年代以来研究较多的微分方程的分支内容.近年来,已有不少的专家学者对泛函微分方程[1]的定性和非定性等相关性质做了分析研究,这些研究包括了周期解的分析[2-3]、有界性的分析[4-5]等,对于无穷时滞和分布时滞等一些类型的方程都做了一定的研究工作.本文主要考虑更一般形式的泛函微分方程,对其周期解的存在性和稳定性进行定性分析,得出了更具一般性的结论,对已有的结果进行了推广和改进.
对于下面两个微分方程
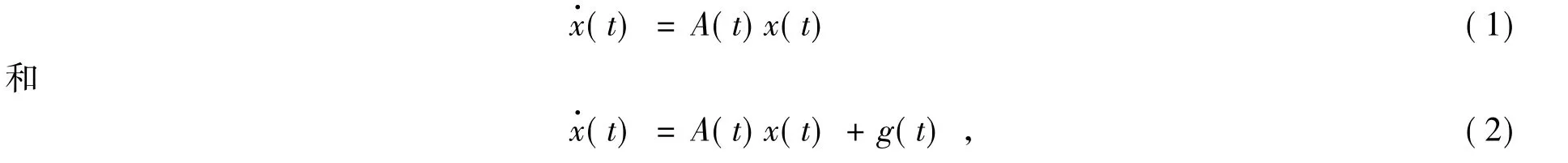
其中:t∈R,x∈Rn,A(t)为n×n连续函数矩阵,且A(t+T)=A(t),g(t)为连续向量函数,且g(t+T)=g(t),关于其基解矩阵有如下的结论.
引理1[6]对于系统(1),假设存在不全为零的T-周期连续向量函数α(t),使得对于∀t∈R,有μ1(A(t))≤α(t)≤0成立,则系统(1)的基本解矩阵X(t)一定满足下面的不等式:
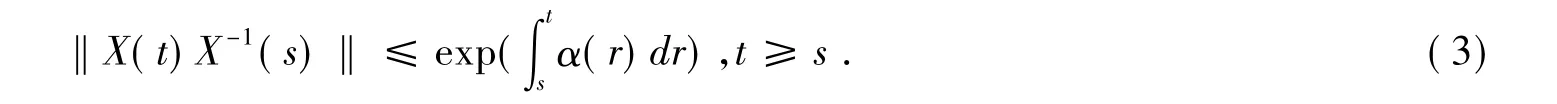
引理2[7]在引理1的条件下,方程(2)存在唯一的T-周期解x(t),它可以用如下式子表示:
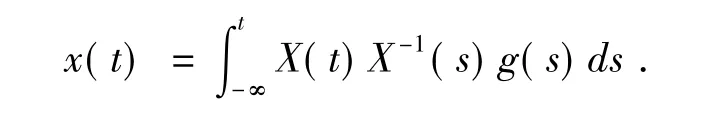
其中X(t)为方程(1)的基解矩阵.
引理3 设C(t,s)为n×n连续的函数矩阵,并且满足假设条件(A3)、(A5),如果f1(t)是连续的T-周期函数向量,则g(t)=t,s)f1(s)ds也是连续的T-周期函数.
1 主要结果
本文考虑如下的中立型无穷时滞泛函微分方程
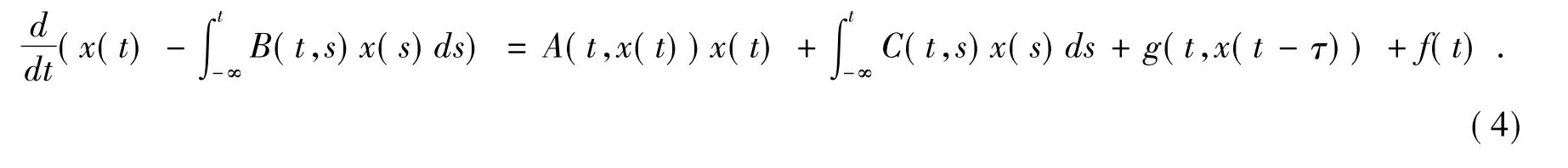
其中:t∈ R,x∈ Rn,A(t,x)=(aij(t,x))n×n,B(t,s),C(t,s) 为n × n 维的连续函数矩阵,g 是从 R × Rn到Rn的连续向量函数,f(t)是从R到Rn的连续向量函数,f(t)是从R到Rn的连续向量函数.
对于上述方程(4)中的函数,先作如下假设:
(A1) A(t,x)和f(t)关于t都是以T为周期的函数,并且有μ1(A(t,x))≤α(t)≤0,其中α(t)是连续的不恒为零的T-周期函数;
(A2) 存在常数K1,0≤K1<1,它使得对 ∀t∈R有B(t,s)‖ds < K1,且对 ∀t,s∈ R 有

定理1 对于方程(4),如果条件(A1)~(A5)成立,则方程(4)存在唯一的T-周期解.
证明 设B={u(t)|u∶R→Rn是连续的T-周期函数},则集合B在范数‖u‖ =sup{‖u(t)‖∶0≤t≤T}下是一个Banach空间.

对t求导可得x(t)满足方程(4),x(t)是方程(4)的唯一T-周期解.
考虑方程
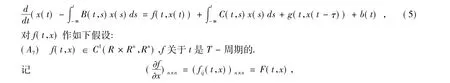
则 F(t,x) 满足(A1).
推论1 如果满足条件(A2)~(A7),则方程(5)存在唯一的T-周期解.
证明 由 f(t,x)∈ C1(R ×Rn,Rn),可知
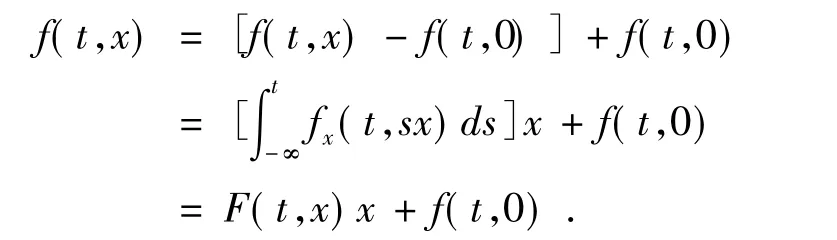
结合假设条件知,方程(5)满足定理1中的相应条件,故由定理1得出方程(5)存在唯一的T-周期解.
考虑方程
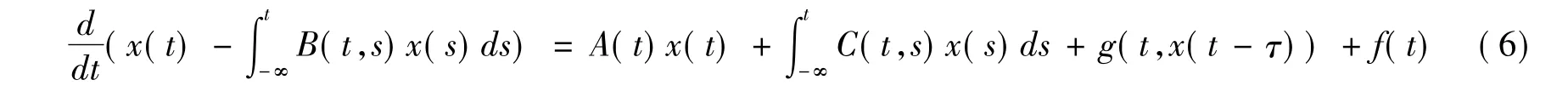
作如下假设:
(A8) A(t)关于t是以T为周期的,且μ1(A(t))≤α(t)≤0,α(t+T)=α(t),其中α(t)不为零.
定理2 如果方程(6)满足条件(A2)~(A6)和(A8),则它一定存在唯一的一致稳定的T-周期解.
证明 类似定理1的证明过程,可知方程(6)存在唯一的T-周期解.下证方程(6)的任一解都是一致稳定的.方程(6)可改写成如下形式

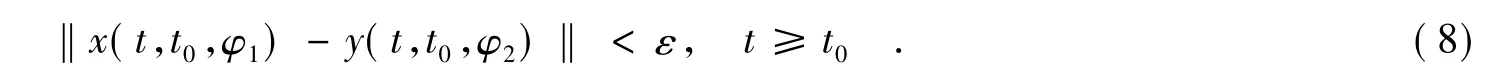
否则,一定存在 t1> t0,使得 ‖x(t,t0,φ1) - y(t,t0,φ2)‖< ε,t0< t<t1,而
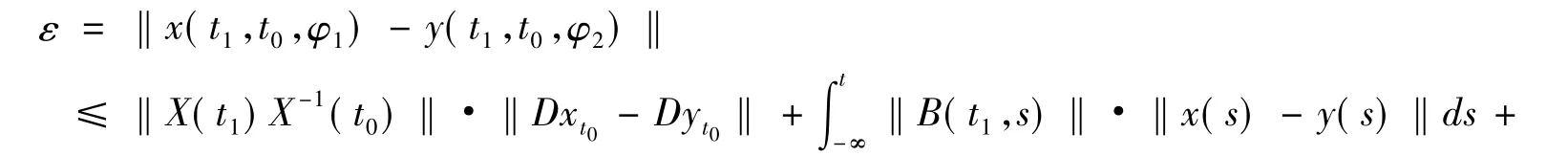
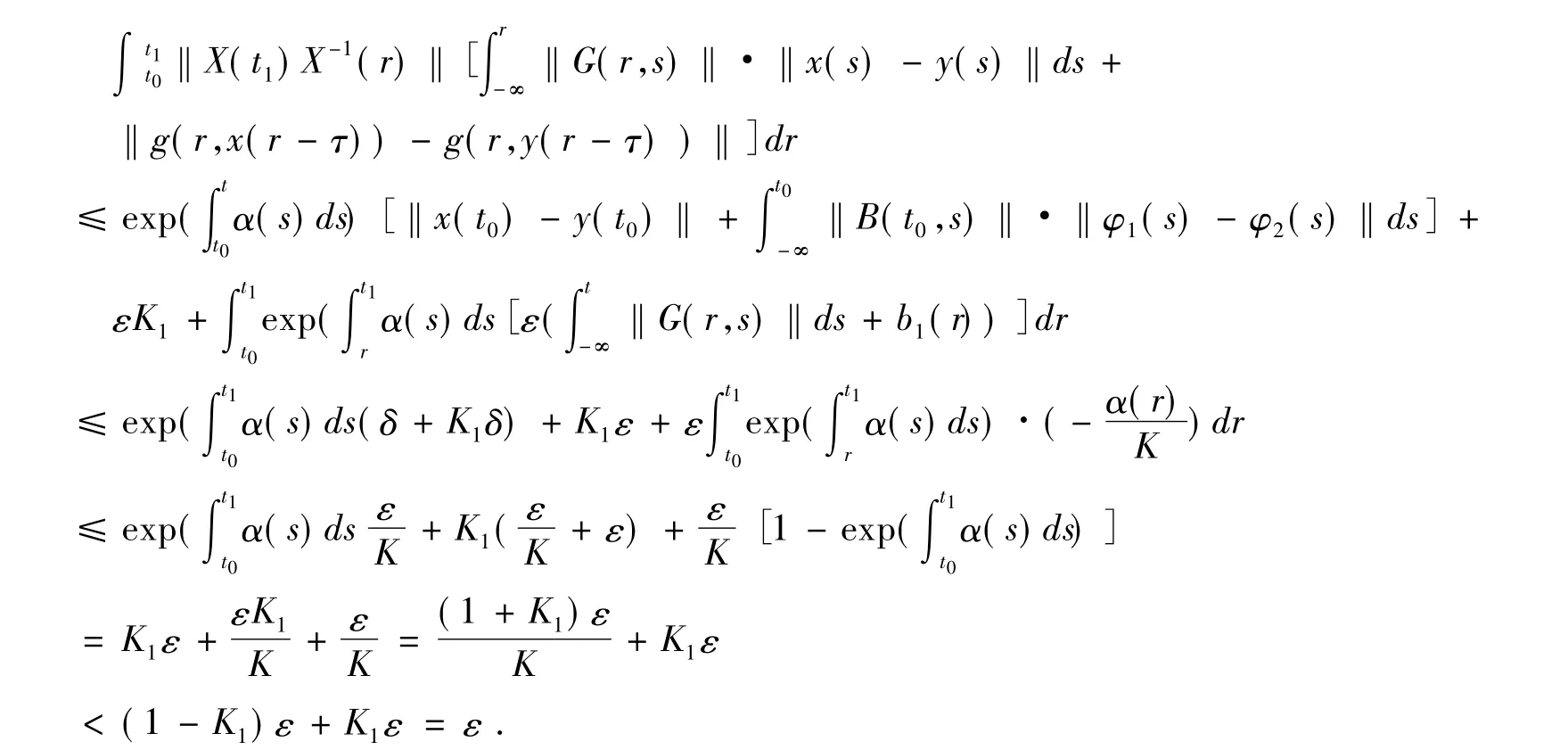
从而得出矛盾,所以(8)式成立.即方程(6)的解是一致稳定的.
[1]郑祖庥.泛函微分方程[M].合肥:安徽教育出版社,1994.157 -168.
[2]张莉,黄先开,葛渭高.一类中立型泛函微分方程周期解的存在性[J].北京理工大学学报,2011,31(12):135-141.
[3]秦发金,姚晓洁.一类高阶中立型泛函微分方程周期解[J].华南师范大学学报(自然科学版),2012,44(1):21-26.
[4]王雯,徐燕,鲁世平.D算子型线性中立型泛函微分方程解的性质[J].安徽师范大学学报(自然科学版),2011,34(1):42-49.
[5]魏克英,王克.无限时滞中立型泛函微分方程解的有界性[J].黑龙江大学自然科学学报,2009,26(5):617-621.
[6]王全义.具有无穷时滞的积分微分方程周期解的存在性,唯一性及有界性[J].应用数学学报,1998,21(2):312-318.
[7]彭世国,朱思铭.具有无穷时滞泛函微分方程的周期解[J].数学年刊(A辑),2002,23(3):371-380.
