一类一阶微分方程初等解法的分析研究

白福梅

（晋中师范高等专科学校，山西 晋中030600）

一类一阶微分方程初等解法的分析研究

白福梅

（晋中师范高等专科学校，山西 晋中030600）

对一阶微分方程变量分离方程f（x）φ（y）（其中f（x），φ（y）分别是x，y的连续函数）和非齐次线性微分方程＝p（x）y＋Q（x）（其中p（x），Q（y）是x的连续函数）的其初等解法进行了分析研究，结合Lebesgue积分与Riemann积分的相关知识，给出了f（x），φ（y），p（x），Q（x）的不连续点集是零测集时的初等解法。

一阶微分方程；变量分离方程；非齐次线性微分方程；零测集

文献［1］中研究了下列一阶微分方程的初等解法：

变量分离方程

其中f（x），φ（y）分别是x，y的连续函数。

如果φ（y）≠0，可将（1）式改写成

两边积分，得到

这里c为积分常数。

如果存在y0使φ（y0）＝0则直接验证y＝y0也是（1）的解。当y＝y0不包括在方程通解（1.1）中时，必须补上特解y＝y0。

一阶线性微分方程

其中p（x），Q（y）在考虑的区间上是x的连续函数。

若Q（x）＝0，方程（2）变为

方程（2.1）称为一阶齐次线性微分方程。若Q（x）≠0，方程（2.1）称为一阶非齐次线性微分方程。

方程（2.1）是变量分离方程，其通解为

这里c是任意常数。

将常数c变易为x的待定函数c（x），令

这里¯c是任意常数。将（2.5）代入（2.2）得到方程（2）的通解。

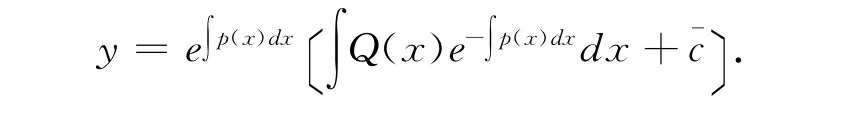
本文将方程（1），（2）中的条件进行了推广。

1 相关知识与理论

定义1［2］设E⊂Rn，若｛Ik｝是Rn中的可数个开矩体，且有

则称｛Ik｝为E的一个L－覆盖，我们称

为点集E的Lebesgue外测度。

推论1［2］若E⊂Rn为可数点集，则m＊（E）＝0。

定义2［2］设E⊂Rn，若对任意的点集T⊂Rn，有

则称E为lebesgue可测集，简称为可测集，其外测度称为测度。

推论2［2］外测度为零的点集是零测集。

引理1［2］设f（x）是定义在I＝［a，b］上的有界函数，记ω（x）是f（x）在［a，b］上的振幅函数，我们有

左端是ω（x）在I上的Lebesgue积分。

引理2［3］（可积的第一充要条件）设f（x）是定义在［a，b］上的有界函数，f可积的充要条件是：f在［a，b］上的上积分等于下积分，即S＝s。

定理1［2］若f（x）是定义在［a，b］上的有界函数，则f（x）在［a，b］上是Riemann可积的充分且必要条件是f（x）在［a，b］上的不连续点集是零测集。

证明 必要性，若f（x）在［a，b］上是 Riemann可积的，则f（x）的Darboux上下积分相等，从而由（3）可知∫Iω（x）dx＝0。

因为ω（x）≥0，所以ω（x）＝0，a.e.x∈［a，b］。这说明f（x）在［a，b］上是几乎处处连续的。

充分性，若f（x）在［a，b］上的不连续点集是零测集，则f（x）的振幅函数ω（x）几乎处处等于零。从而由（3）可知

即f（x）的 Darboux上下积分相等，f（x）在［a，b］上是 Riemann可积的。

2 主要结论

变量分离方程

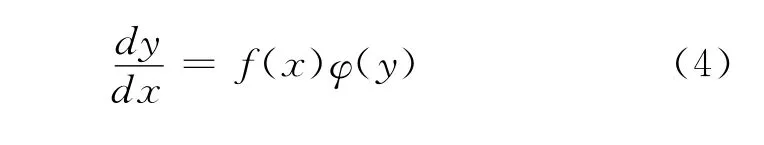
其中f（x），φ（y）分别在［a，b］上是有界函数，关于x，y的不连续点集是零测集。

如果φ（y）≠0可将（4）式改写成

这里c为积分常数。

如果存在y0使φ（y0）＝0，则直接验证y＝y0也是（4）的解，当y＝y0不包括在方程的通解（4.1）中时，必须补上特解y＝y0。

一阶线性微分方程

其中p（x），Q（x）在［a，b］上是有界函数，关于x的不连续点集是零测集。

若Q（x）＝0，方程（5）变为

方程（5.1）称为一阶齐次线性微分方程.若Q（x）≠0，方程（5）称为一阶非齐次线性微分方程。

方程（5.1）是变量分离方程，其通解为

这里c是任意常数。

将常数c变易为x的待定函数c（x），令

这里¯c是任意常数，将（5.5）代入（5.2）得到方程（5）的通解

［1］王高雄，周之铭，米思铭.常微分方程［M］.北京：高等教育出版社，2006：30－48.

［2］周民强.实变函数论［M］.北京：北京大学出版社，2001：80－200.

［3］华东师范大学数学系.数学分析［M］.北京：高等教育出版社，1991：284－288.

For the separation of variable equation＝f（x）φ（y），where f（x），φ（y）are continuous function of"x，y"，as well as non－homogeneous linear differential equations of first－order differential equations＝p（x）y＋Q（x），where p（x），Q（y）is continuous function of x.In this paper，the elementary solution was analyzed，combined with Lebesgue integral and Riemann integral related knowledge，the elementary solution was given when the discrete point set was zero test set.

First order differential equations；Variable separation equations；Non－homogeneous linear differential equations；Zero measurable set

Elementary Solution to a Kind of First－ Order Differential Equation

Bai Fumei
（Jinzhong Teachers College，Shanxi Jinzhong 030600，China）

O175.29

A

1671－8151（2012）05－0478－03

2012－05－11

2012－05－29

白福梅（1976－），女（汉），山西柳林人，硕士，研究方向：运筹学与控制论。

（编辑：马荣博）