肖维勒准则和格拉布斯准则的比较

2012-09-19林丽芬吴先球

大学物理实验 2012年6期

林丽芬，肖化，吴先球

（华南师范大学，广东广州 510006）

实验测量的数据中有时会发现个别数据与其他数据差异很大（过大或过小），这是由于实验过程中出现某种差错或者环境条件突变造成的，文中称为异常数据。对于一组实验中异常数据的取舍，如果将混有异常数据的实验数据进行实验结果计算，会加大实验误差，甚至是歪曲实验结果，因此要将这些异常数据剔除，以符合客观事实。但不能为了得到精度更高的结果，而任意地把一些误差较大、但符合测量值随机波动性而含有正常偏差的数据剔除[1，2]。

本文以《测直流电源的电动势和内阻》为例，利用Origin软件进行实验数据线性拟合的功能，分别以肖维勒准则[1]和格拉布斯准则[2]实现异常数据的判断和剔除，并比较两种准则使用范围的差异。

1 肖维勒准则和格拉布斯准则

1.1 肖维勒准则

在n次测量中，取不可能发生的个数为0.5，那么对正态分布而言，误差不可能出现的概率为

利用标准正态函数表，根据等式右端的已知值n可查表求出肖维勒系数ωn。对于数据点xd，若其残差Vd满足Vd＞ωnσ则剔除，否则xd应保留。其中σ是样本标准差。

1.2 格拉布斯准则

设n个测量值按大小顺序排列x1≤x2≤…≤xn，假设xn是需要检验判别的异常数据。S和Sn都是测量值的函数，对应的概率密度为

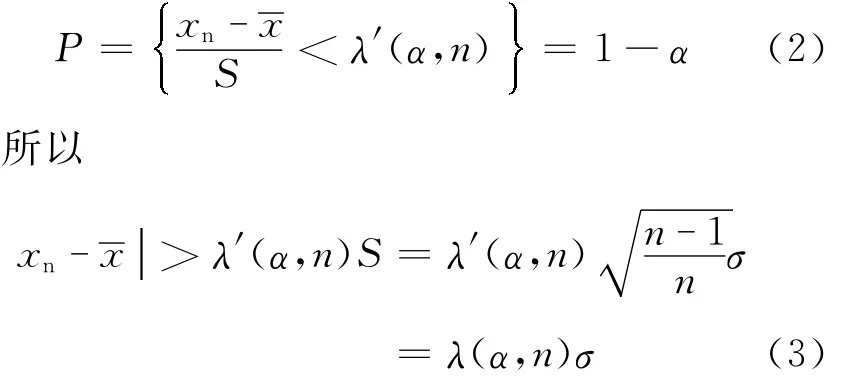
通过查表可得λ（n，α）值，根据异常数据xn与平均值的残否大于λ（n，α）倍样本标准差σ来判断异常数据是否应当剔除。

2 用Origin实现实验数据的剔除[4]

首先将伏安法测得外电路的电流和电压的实验数据如表1所示[5]。

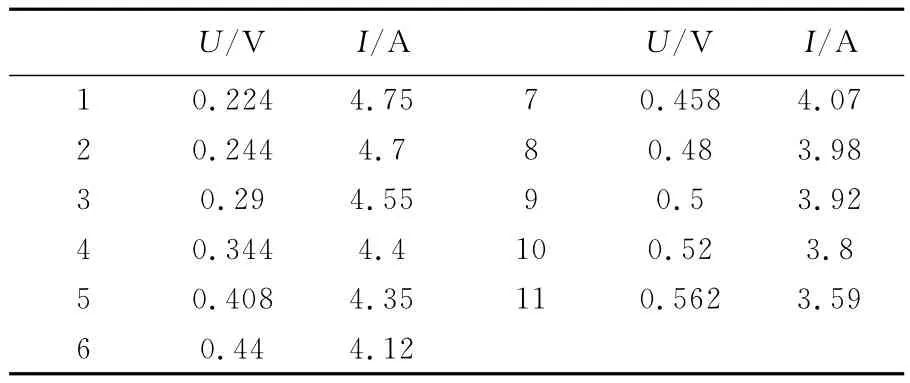
表1 实验数据

输入到Origin的工作表Worksheet中，生成二维坐标数据点状分布图，调用Origin内置的最小二乘法线性拟合工具，如图1所示。

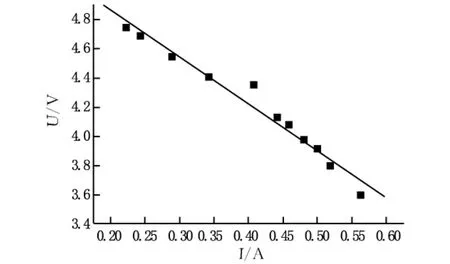
图1 原始数据线性拟合结果

由图1可看出，测量数据中第5、11点离拟合直线偏差较大，是异常数据。通过Column／Add New Column新增一列，命名为Vd，存放残差。调出script window 执行命令：Data1＿Vd＝5.51444＋Data1＿I＊（-3.22794）－Data1＿U；得到Vd列的值。

2.1 用肖维勒准则判断

当n为11时，ω11为2.00。新增一列，命名为Contrast1，该列执行命令：

Data1＿Contrast1 ＝ abs（Data1＿Vd）－2.00＊0.06865；

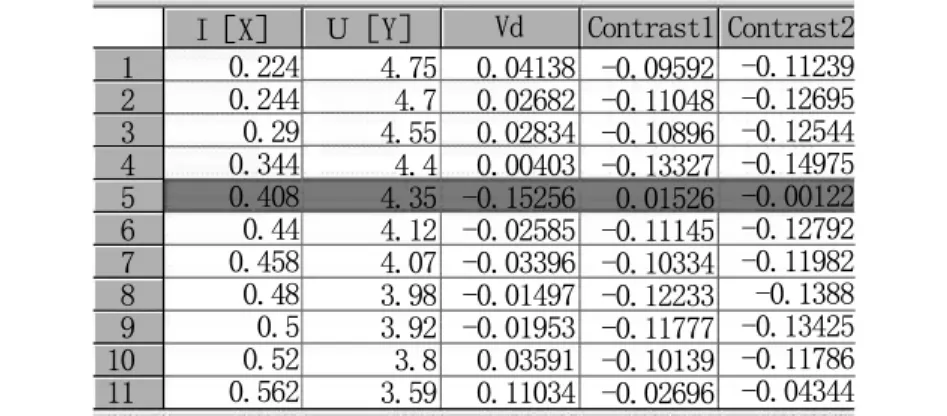
图2 肖维勒准则和格拉布斯准则与残差的比较结果对比

2.2 用格拉布斯准则判断

当n为11时，λ（11，0.05）为2.24。新增一列，命名为Contrast2，该列为行命令：

Data1＿Contrast2＝abs（Data1＿Vd）－2.24＊0.06865；

如图2所示，Contrast2所有数值都为负值，即所有的数值都是符合统计学概率而出现的。

2.3 讨论

两个准则的判别结果如图2所示，但相互矛盾的结果并不能说明肖维勒准则比格拉布斯准则的保留数据较窄，从而认为前者比后者更可靠。虽然两个准则都与测量次数挂钩，但肖维勒准则存在明显缺点：n不同时，置信水平就不同；而格拉布斯准则可根据研究对象的特点，选择合适的置信水平进行讨论。肖明耀[1]、吴先球[2]等人都提到格拉布斯准则的剔除原则同时与测量次数、显著性水平联系起来，并适用于n＜100的情况，对样本中仅混入一个异常数据的情况判别效率最高[3]。

首先，在本例中测量样本比较小，两种准则的标准差因偏离正态分布而不准确，但σ由Origin软件中的内置程序处理所得，数值相等，可信度高。忽略标准差存在的误差。

其次，两个准则判断是否为异常数据时，都满足

k是统计临界系数。对应于相同的测量次数，两准则的统计临界系数各不相同，而判断结果对统计临界系数相当敏感。在同一k值下（k＝3）格布拉斯准则对应的测量次数n＝25（α＝0.01）、n＝50～60（α＝0.05），而肖维勒准则是185。

第三，格拉布斯准则在相同的k值下，置信水平不同（0.01、0.025、0.05三个置信水平），n值有所不同。n相同时，λ（n，0.01）比λ（n，0.05）大，即α＝0.01比α＝0.05的保留数据窄，说明σ在一定时，α值越小，对异常数据剔除的要求更严格，有效避免错误剔除包含正常误差或保留了含有粗大误差的数据。

最后，针对实际的测量次数选择合适准则，确保正确地剔除坏值，保留好值。在统计临界系数k＝3时，肖维勒准则的系数ωn随n（n＜185）相对格拉布斯准则的系λ（n，α）数随n（n＜25）的变化小，即格拉布斯准则的系数λ（n，α）对测量次数n（n＜25的变化比较敏感[3]。在本例中测量次数n＝11，ω11＝2.00比λ（11，0.01）＝2.48小，容易剔除含有较大正常误差的测量值。

因此，文中《测直流电源的电动势和内阻》的11组原始数据中，第5个数据是否剔除，应当采用格拉布斯准则（置信水平α为0.01）不剔除这个数据，虽然σ会偏大，但结果相对安全且符合统计学规律。