基于MatIab分析数据和传感器控制的金属杆的线膨胀与温度关系的实验研究
2012-09-19刘雅彬夏雪琴
刘雅彬,夏雪琴
(浙江海洋学院,浙江 舟山 316000)
在大学物理实验中存在许多非电学量,需要用到多种传感器进行检测和控制。若能改变实验设备及内容,恰当选择和合理使用传感器,将传感器运用于大学物理实验中配以相应的接口电路与计算机终端,将在很大程度上优化实验过程、保证实验效果、提高仪器性价比[1]。
以往在大学物理实验中,传统的做法只能测量金属矸的线膨胀系数,很难证明线膨胀与温度变化的正比关系。本文以电脑控制热膨胀系数的实验为例,如图1所示,运用了Matlab的数据处理功能在一定程度上简化了数据处理的过程,从而得到金属杆的线膨胀是与温度变化成正比关系。

图1 金属杆的线膨胀与温度的关系的实验示意图
1 实验原理
1.1 金属杆的线膨胀与温度的关系
原长度为L的固体受热后,其相对伸长量ΔL正比于温度的变化,即[2]:

设在温度0℃,t1℃、t2℃ 时固体的长度分别为L0、L1、L2,由式(1)可得

由(2)、(3)两式解得:
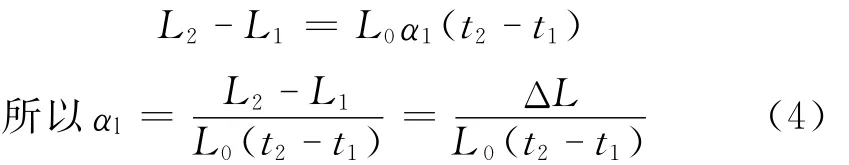
从式(4)可知,对同一个金属杆而言,当温度从t1升至t2时,其伸长量ΔL与温度的变化成正比。
1.2 用力传感器测微小的长度变化ΔL
力传感器的工作原理是在传感器内部有一个弹性应变片,当应变片受力发生形变时显示出相应的电参数变化。因应变片的形变是在其弹性形变的范围内,根据胡克定律,形变量与受力成正比。所以力传感器显示的受力大小也代表了它自身的形变大小。金属材料的线胀系数通常都很小(约105/℃数量级),在数十度的温度变化范围内,一根20~30cm的金属杆的伸长量仅零点几毫米。对于这样微小的长度变化用一般的长度测量仪器是难以准确测量的。为此,在本实验中选用力传感器达到测量微小长度变化的目的,且传感器测出的形变量可以从电脑屏幕上实测显示出来。
1.3 加热装置控制温度的变化
由于在实验中的传感器的加热装置是集成的,而从内部的原理来看,加热装置的加热时能力是有能量和时间关系的,又温度计的数值可以读出在时间上,两者基本上是呈线性关系的;从外部关系上来说,在金属丝的外围仍有着较好的绝热装置,在金属丝的伸出端还有有机玻璃的部件防止散热,在试验的过程中也没有部件的移动,及外部空气的对流,实验室的外部环境也基本保持稳定。所以在有关金属丝的温度与时间关系上可以认为是一阶线性的。由实验原理知,我们在20~30、30~40、40~50℃左右的三个区间内来进行数据采集。
从上面的分析可知金属杆线膨胀与漫长的关系转化为金属杆线膨胀伸长后给力传感器的压力随温度变化的关系。
2 实验方案
(1)将被测试样品安装在测试架上,把金属杆的伸长端通过一只杠杆顶在力传感器上。打开电脑上的力传感器的应用软件,从电脑屏幕上即可显示出受热后的样品给力传感器压力情况。在开始时,力传感器应校准。
(2)在加热电源箱的面板上,温度的升高速度有高、中、低三种选择。如果要使电脑显示的温度与金属杆的真实温度尽可能接近,可选择低速加温;若想加快实验的速度则可选择快速加温。
(3)打开加热电源开关,金属杆被加热后温度开始上升。经力传感器采集数据,电脑屏幕上就会显示金属杆伸长后给力传感器的压力随温度升高的变化数据。
3 实验数据分析与处理结果
3.1 传感器采集的数据
部分具体的数据如下(前40组)见表1。

表1 实验数据

组数 时间 压力 组数 时间 压力10 12.62 0.04 20 26.62 0.15 21 28.02 0.15 31 42.02 0.22 22 29.42 0.15 32 43.42 0.22 23 30.82 0.15 33 44.82 0.22 24 32.22 0.15 34 46.22 0.26 25 33.62 0.15 35 47.62 0.26 26 35.02 0.15 36 49.02 0.26 27 36.42 0.19 37 50.42 0.26 28 37.82 0.19 38 51.82 0.26 29 39.22 0.22 39 53.22 0.3 30 40.62 0.22 40 54.62 0.3
3.2 MatIab的拟合处理
传感器的数据是0.02s采集一次的,采集由时间和力传感器的采集数据所组成。由力探测头得到的金属丝由加热产生的微小变量通过力传感器内部的弹性传动装置产生力的变化信号,从而转化成为数字信号进入到计算机。但是我们每组数据计算大约五分钟的值,这样每组数据有15 000个,以平时的运算方式很难处理,因此用Matlab来进行分析[3-5]。
Matlab进行数据的拟合,设y为压力,x为时间,程序如下:
a=data(:,1);
b=data(:,2);
A=polyfit(a,b,2);
z=polyval(A,a);
plot(a,b,a,z)
A=
-0.0000-0.006 1 0.032 4
由此可知,其函数关系为

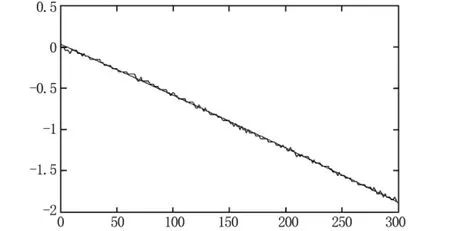
图1 Matlab进行数据处理的压力与时间的线性拟合图
3.3 MatIab的拉格朗日插值的辅助误差估计
对于Matlab的拉格朗日插值运算来说,我们对于在如此近似线性的数据组中,如果做15 000次的数据运算不仅没有必要,而且计算机的处理时间也太长,实际运算中我用了两个小时,还没有得到结果,因此我们选用15 000中的215组(以70个数据中选一,做等差选择Ecxel处理)来进行二次处理,实际运用中效果较好,且不影响数据的处理程度。然后用拉格朗日的插值,来初步的估计误差[6]。
Matlab的拉格朗日插值法:
function y=lagrange(x0,y0,x);
n=length(x0);m=length(x);
syms z
for i=1:m
z=x(i);
s=0.0;
for k=1:n
p=1.0;
for j=1:n
if j~=k
p=p*(z-x0(j))/(x0(k)-x0(j));
end
end
s=p*y0(k)+s;
end
y(i)=s;
end
如图3,实际的插值结果如下,

图3 拉格朗日插值截图
拉格朗日插值的辅助误差估计可知,只有前3个数据有误差以外,其余的实验误差几乎为零。
3.4 线性度误差的MatIab计算
Matlab程序的设计如下:
c=length(data(:,1));
k=-1.89/299.6;
v0=0
for i=1:c
v1=(data(i,2)-k*data(i,1))/((1+k^2)^(1/2)*299.6);
if abs(v1)>v0;
v0=v1;
end
end
v1
计算结果为
v1=
4.2111e-007
由此可知,在线性拟合度误差的结果上,在10的-7次方的数量级上,因此此数据的线性度极高,绝对符合实验的要求。
3.5 实验结果
由Matlab分析数据和拉格朗日插值的辅助误差估计,从而验证了传感器控制的金属杆的线膨胀与温度变化绝对成正比关系的。
4 结 论
以往我们做这个实验都是测出金属杆的线膨胀系数,没有从根本上验证金属杆的线膨胀与温度变化的正比关系。通过传感器控制的金属杆的线膨胀与温度关系的实验研究,有了传感器的装置使实验数据的采集更为方便简洁,实验的数据分析运用了Matlab数据拟合和拉格朗日插值的辅助误差估计,从而验证了传感器控制的金属杆的线膨胀与温度变化绝对成正比关系。
[1]黎敏,廖延彪.光纤传感器及其应用技术[M].武昌:武汉大学出版社,2008.
[2]竺江峰,芦立娟,鲁晓东.大学物理实验[M].北京:中国科学技术出版社,2005,9.
[3]苏金明,王永利.MATLAB7.0实用指南[M].北京:电子工业出版社,2004.
[4]刘瑞华,李力.V基于MATLAB的数据采集系统设计研究[J].工业控制计算机,2003,16(7).
[5]韩进宏.互换性与技术测量[M].北京:机械工业出版社,2004,7.
[6]张德丰.数值计算方法[M].北京:机械工业出版社,2010,1.
