改进的Turbo类编码的近似码字错误率公式
2012-09-19戴利云杨鸿文尧文元
戴利云 杨鸿文 尧文元
①(江西财经大学软件与通信工程学院 南昌 330013)
②(北京邮电大学信息与通信工程学院 北京 100876)
1 引言
自从Berrou等人[1]提出Turbo码以来,基于迭代译码思想的Turbo类编码已成为现代信道编码的主流,其中包括Turbo码,LDPC码[2],RA码[3],PA码[4]等等。然而,对于此类编码,其理论错误率目前还是未知的。研究中一般采用蒙特卡罗仿真的方法来得到错误率的估计值,但这种方法对无线通信中的许多应用来说(例如链路级与系统级的仿真接口[5])极不方便,同时,也不利于揭示问题的理论本质。
在无法获得Turbo类编码的理论错误率的情形下,许多研究者转而采用错误率的界[6-8]的方法来对其进行估计。这些界对于人们深入理解这些码的特性起到了非常重要的作用,对码的设计也有重要的指导意义,但对于某些实际应用(例如文献[9,10])来说这些界还比较松散。另外,大部分关于界的研究都基于最大似然译码,因此,从理论上来说,这些界不能体现对实际系统相当重要的一些译码设计上的差异,例如Turbo码的Log-MAP及其各种简化算法、迭代次数等因素[11,12]。另一方面,用界来估计错误率还需要已知码重谱。对于任意的Turbo码或者LDPC码来说,准确测定码重谱也非易事。此外,也有不少研究者应用重要采样法或其他方法[13,14]来估计错误率,对于Turbo码和LDPC码来说,这些方法的通用性或者估计精度都不够理想。
在错误率估计方面,文献[15]中提出了一种新的思路,就是利用判决域的平方半径谱来估计。文献[15]还给出了一个简单的错误率近似公式。本文主要工作是对文献[15]中的近似公式进行了改进,使误差从0.2 dB缩小到0.05 dB。同时,由于近似公式中有两个参数必须通过仿真来测定,其统计误差是影响近似公式准确度的重要因素,因此本文另一项工作是分析研究由此引起的误差问题。结论表明,只需测量几百条半径样本,就能使得误码率为1%时对应的信噪比偏差控制在±0.05 dB之内。
本文第2节导出所提的近似公式,第3节分析参数误差问题,第4节给出结论。本文用大写粗斜体U表示随机向量,用大写斜体V表示随机变量,用小写粗斜体u和小写斜体v分别表示随机向量U和随机变量V的实现。
2 基于判决域半径的错误率近似公式
考虑BPSK调制及AWGN信道。由于(n,k)编码器的输入信息的随机性,编码调制后的发送信号S=(S1,…,Sn)是一个随机向量。对于BPSK调制,可假设Si∈{±1},i=1,…,n。编码器的约束关系使得随机向量S只能取值于样本空间S⊂nℝ ,其元素个数为2k。译码器的输入可以表示为

其中高斯噪声Z=(Z1,…,Zn)的元素Zi独立同分布,其均值为0,方差为σ2。本文用记号β=1/σ2表示信噪比。
译码器将Y的样本y映射为译码结果
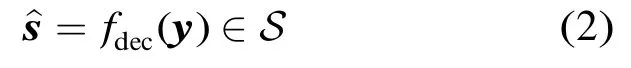
对于每个发送的s∈S,所有译码结果为s的y的集合构成了s的判决域
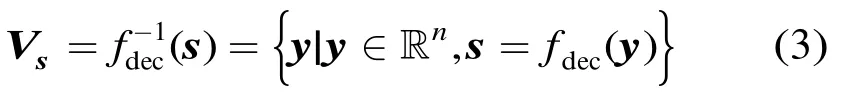
发送s条件下的译码错误率就是Y=s+Z落在Vs之外的概率,即
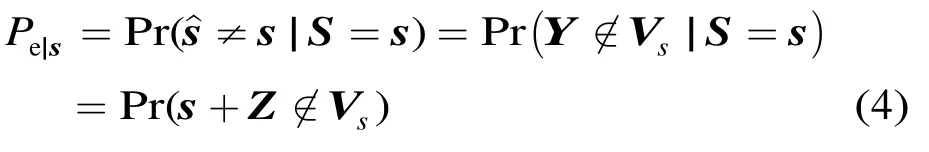
平均译码错误率是所有s的错误率的平均值,即Pe=E[Pe|s]。对于线性编码、BPSK调制及ML译码,所有s有相同的错误率。对于Turbo码和LDPC码的迭代译码,也基本上可以这样认为。故此,为简单起见,以下始终假设发送信号S固定为s,并用Pe代替Pe|s。
参考图1可知,式(4)中的随机事件“s+Z∉Vs”等价于随机事件“噪声的长度大于判决域半径R”,因此
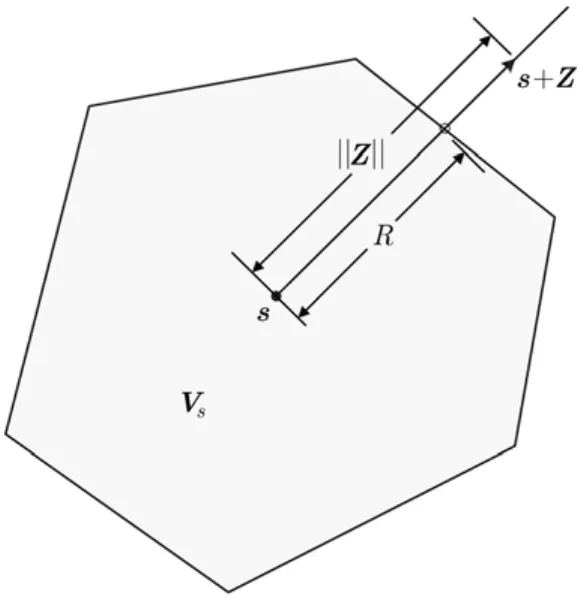
图1 判决出现错误表明噪声长度超过了噪声方向上的判决域半径
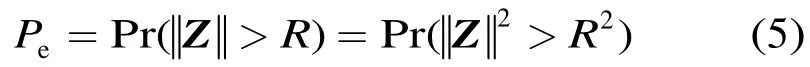
根据中心极限定理,当n充分大时近似服从高斯分布。容易求出的均值为n/β,方差为 2n/β2。另外根据仿真观察,式(5)中的R2也可近似为高斯分布,图2示出了两个实测的例子。关于R的样本的测量问题,参考图1可知测量方法就是对随机择定的信号s及噪声样本z,逐步加大噪声的长度,直至译码开始出错。因为是一维搜索,故此可以用二分法等方法快速进行。需要注意的是,虽然对于所假设的AWGN信道及BPSK调制,ML译码器不需要已知信噪比β,但Turbo码的Log-Map译码算法[12],LDPC码的sum-product译码算法(SPA)[16]在把y映射为信道软信息时,需要知道噪声的方差:

对此,测量半径时可以用搜索进程中实际的噪声长度来代替,即,若送入译码器的是s+z,则信道软信息用下式给出的值:
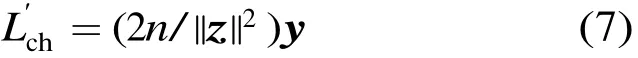
图2中测量半径时所用的Turbo的定义见文献[10],其码长n=1152,码率k/n=1/2,分量RSC编码器的生成多项式为[13,15]8,译码采用最大迭代次数为8的Log-Map译码算法;LDPC码采用文献[9]中定义的码长为1152,码率为3/4的码,译码采用最大迭代次数为25的分层SPA译码算法。图2中的每条概率密度曲线都是用随机实测的105个R2样本得出的,图中还同时示出了对应均值和方差相同的高斯分布概率密度。可以看出,R2的概率密度基本符合高斯分布。在其他条件下(不同码长、码率、译码算法、迭代次数等),也可以得到类似的结果。
假设R2可近似为高斯分布,令c1=E[R2],c2=Var[R2]。注意到噪声的长度和判决域半径相互独立,于是也是一个高斯随机变量,其均值为c1-n/β,方差为c2+ 2n/β2。因此,式(5)可以表示成
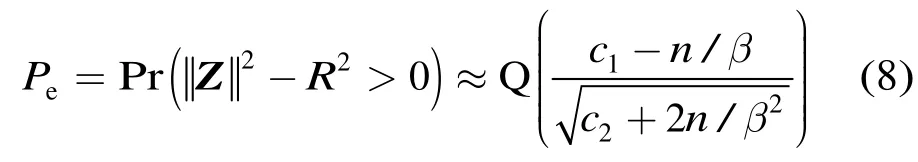
若近似认为是常数,则可忽略式(8)分母中的2n/β2,从而得到
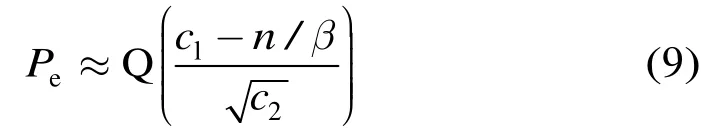
此即文献[15]的式(6),差别只是文献[15]中对平方半径按码长进行了归一化。
图3示出了Turbo码和LDPC码的蒙特卡罗错误率仿真结果以及式(8),式(9)给出的近似结果。此图中的编码和译码算法与图2相同,对每个蒙特卡罗仿真值需要统计到100个码字错误。从图3中可以看出,式(9)的近似误差是0.2 dB,改进后的式(8)的近似误差小于0.05 dB。
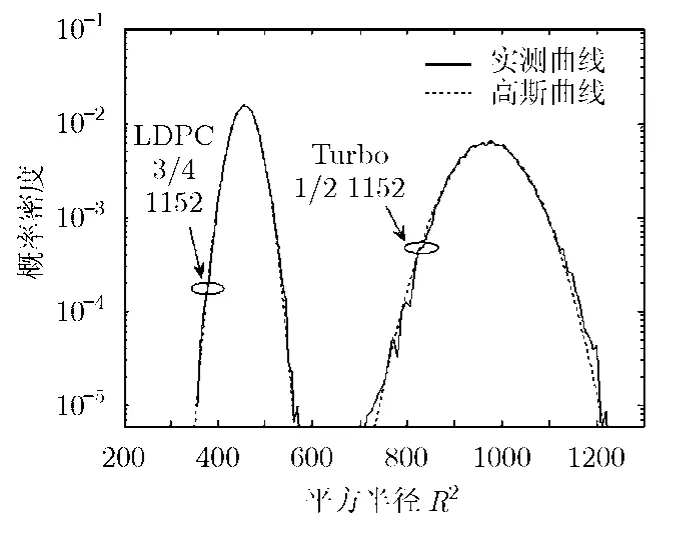
图2 码长1152 码率1/2的Turbo码和码长1152 码率3/4的LDPC码R2的概率分布
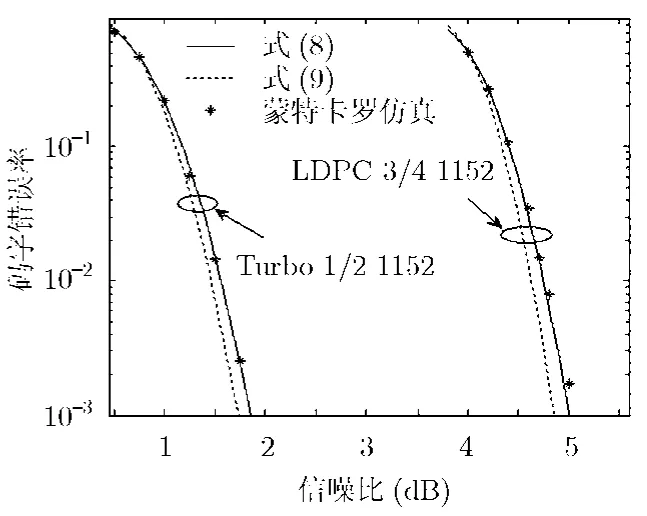
图3 用不同近似公式估算Turbo/LDPC码的错误率
在其他条件下也可以得到类似的结论。表1列出了部分编码/译码条件下的参数值c1,c2。表中LDPC码译码的最大迭代次数均为25,Turbo码的最大迭代次数均为8。需要指出的是,式(8)这个近似式依赖于R2的高斯近似。这一点对于性能较差的短码(如一般的BCH码、约束长度较小的卷积码等)并不成立。另外对于Turbo类编码,如果存在明显的错误率平台(error floor),上述高斯近似的半径分布也无法正确体现处于最小码重一带的判决域结构特性。一般可以通过优化设计来避免或降低平台[17,18]。此外,在具有严重突发衰落的信道中,由于此时译码性能很差,其判决域平方半径也不能近似为高斯分布。对此情形,编码应用中一般会采用信道交织器。我们通过仿真观察到[19],对于独立衰落的理想交织信道,R2仍能较好地近似为高斯分布。总之,对于诸如3G,LTE等中的应用来说,如果信道编译码的设计中已经考虑了误码平台和突发衰落的问题,则所提近似公式的精确程度一般是可以接受的。
3 误差分析
实际应用式(8)时,误差的来源除了高斯近似这个固有因素外,还有一个重要的误差来源是参数c1,c2的测量误差。这是因为c1,c2不仅与码的结构(如LDPC的H矩阵)有关,还与译码器有关。给定一种编码,译码器方面的任何涉及性能的变化,如LDPC译码中的迭代次数、校验节点的更新方式(例如SPA,MSA(Min-Sum Algorithm),offset-MSA等)的改变都会体现为不同的c1,c2数值。因此一般来说,这两个参数只能通过仿真测量来获得。于是,在应用式(8)时,我们只能用基于M个样本的样本均值
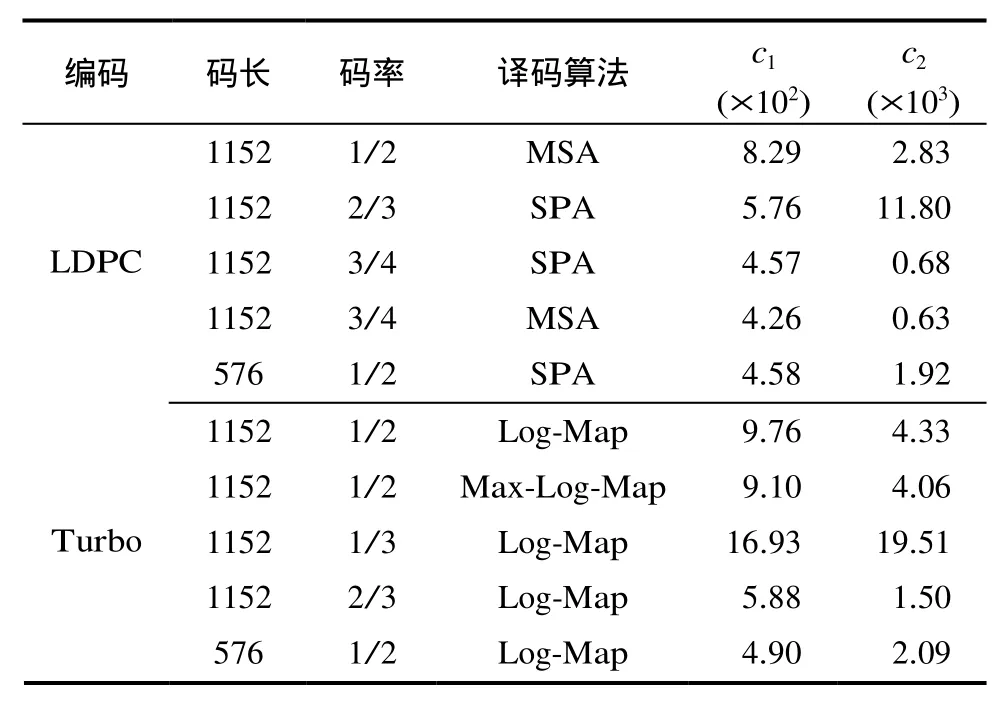
表1 部分编码的c1,c2参数

及样本方差

来近似c1=E[R2]及c2=E[R4]-。当样本数趋于无限时,样本平均将收敛到数学期望,但如果所需的M过大,式(8)将失去意义。因此本节分析样本数M与式(8)的误差之间的关系。
先假设c2准确。对式(8)应用全微分公式可得
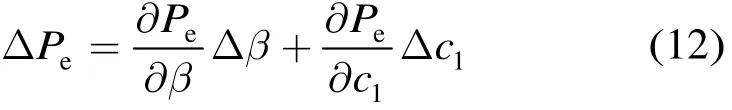
其中ΔPe,Δβ,Δc1分别为错误率Pe,信噪比β和参数c1的绝对变化量。令式(12)中ΔPe=0,可以得到误差关系为

同理可得

式(13),式(14)给出了允许的信噪比偏差为δβ时,对参数c1,c2的误差要求。对于前述的Turbo码和LDPC码,图4示出了不同信噪比偏差下的误差要求,其中Turbo码的信噪比β=1.5 dB,LDPC码中β=4.7 dB时,这两个信噪比大致对应码字错误率为1%左右。用式(13),式(14)计算图中的曲线时,我们用104个样本的测量结果,来代替式中的c1,c2。
根据这个结果可以求得所需的样本数。假设要求的置信度为pΔ,则
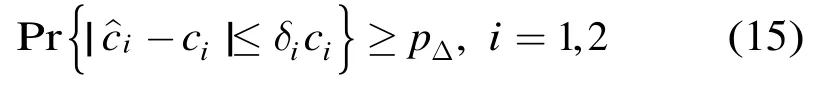
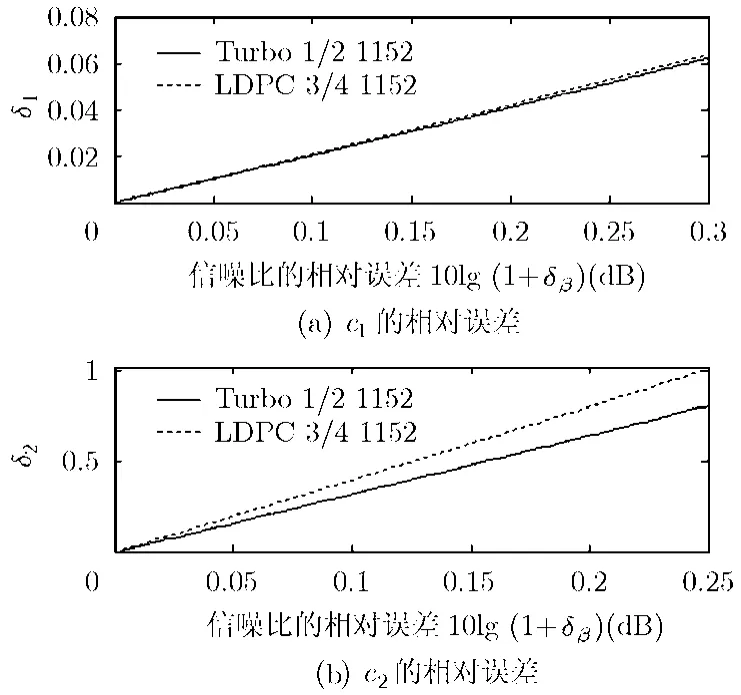
图4 给定信噪比的允许偏差时,参数c1,c2的相对误差
故此由式(15)可得到,当参数ci的允许误差为δi,置信度要求为pΔ时,所需的样本数为
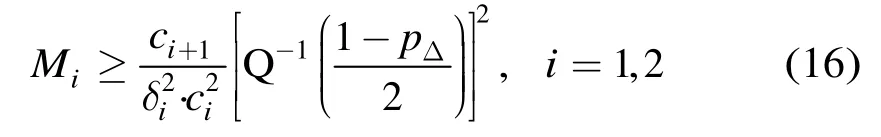
其中 Q-1(⋅)是 Q(⋅)的反函数。
实际所需样本数应取M1,M2的最大值,即
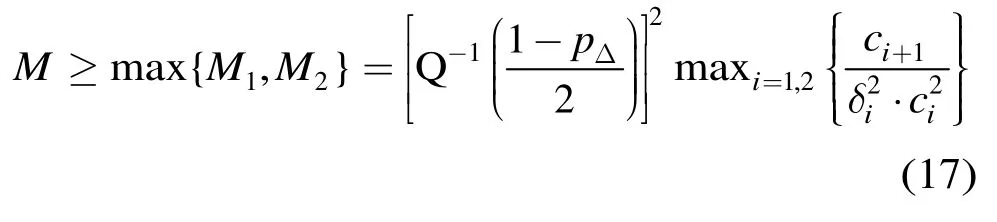
将式(13),式(14)代入式(17),即可得到给定信噪比偏差时,所要求的样本数。图5给出了置信度为90%时,不同信噪比偏差所要求的半径样本数。此图的其他条件与图3相同。
作为进一步的验证,图6给出了一个示例,我们先随机测量出104个Turbo码判决域半径样本,然后用其中的前M个来估计c1,c2,再代入近似式(8)得到错误率的估计值(β,M)。图中示出了信噪比为β=1.5 dB时,(β,M)随M的变化实例,图中还同时给出了信噪比偏差±0.05 dB时,用全部样本所估计的错误率(β⋅ 10±0.005,104)。在这个实例中,错误率估计值误差为0.05 dB时所需的样本数大约是200,在数量级上与图5给出的M值相当。注意图6是用随机M个样本得到的曲线,因此据此图所得到的数值200对于不同的样本排列而言是一个随机量。
类似地,图7中示出了信噪比β=4.7 dB时,LDPC码的码字错误率随样本数收敛的曲线。从图6,图7我们注意到,半径样本数超过1000后,错误率估计值与蒙特卡罗仿真的误差基本保持稳定,也即是,增加样本数对近似公式精度的改善是有限的。
综上所述,对于设计合理的Turbo类编码(误码率平台低于工作点、有适当的信道交织能避免严重的突发差错),如果能够接受±0.05 dB的误差,那么式(8)即是一个可以接受的近似式,并且确定式中的两个参数c1,c2只需要测量数百条半径即可。
4 结束语
文献[15]提出了一种用判决域半径来估计错误率的方法,并提出了一个简单的错误率近似式。本文给出了一个更为精确的改进近似式,并分析了测量参数所需要的样本数。结论表明,对于设计合理的Turbo类编码,在多数无线通信系统所关注的错误率区间内,仅用数百条半径样本即可获得足够准确的参数值,并且近似式所给出的错误率估计值相对于蒙特卡罗仿真结果的偏差可以小于0.05 dB。
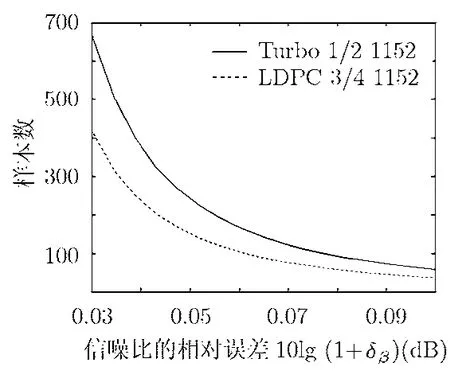
图5 信噪比的相对误差与样本数的对应关系
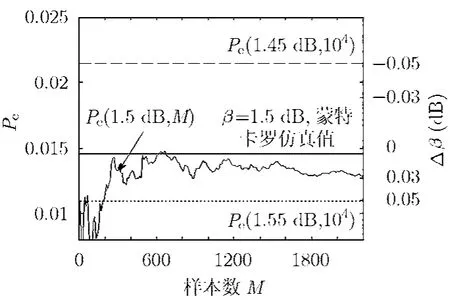
图6 Turbo 1/2 1152码的码字错误率随样本数收敛曲线
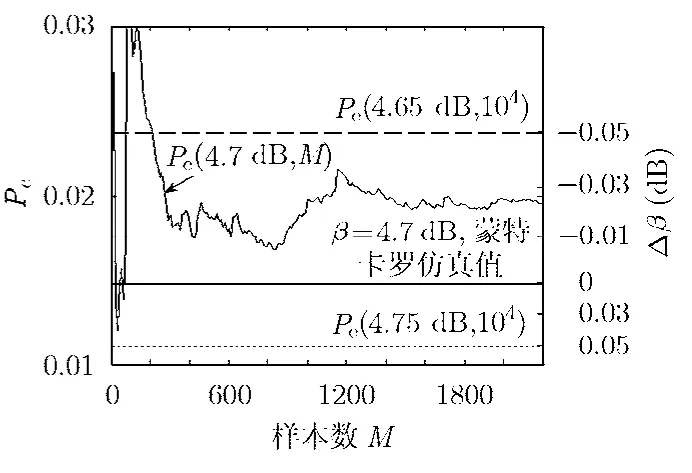
图7 LDPC 3/4 1152码的码字错误率随样本数收敛曲线
[1]Berrou C,Glavieux A,and Thitimajshima P.Near Shannon limit error-correcting coding and decoding: Turbo-codes(1)[C].IEEE International Conference on Communications(ICC),Geneva,Switzerland,May 1993: 1064-1070.
[2]Gallager R G.Low-Density Parity-Check codes[J].IRE Transactions on Information Theory,1962,8(1): 21-28.
[3]Abbasfar A,Divsalar D,and Yao K.Accumulate-repeataccumulate codes[J].IEEE Transactions on Communications,2007,55(4): 692-702.
[4]Li J,Narayanan K R,and Georghiades C N.Product accumulate codes: a class of codes with near capacity performance and low decoding complexity[J].IEEE Transactions on Information Theory,2004,50(1): 31-46.
[5]Chen L,Chen W W,Wang B,et al..System-level simulation methodology and platform for mobile cellular systems[J].IEEE Communications Magazine,2011,49(7): 148-155.
[6]Twitto M,Sason I,and Shamai S.Tightened upper bounds on the ML decoding error probability of binary linear block codes[J].IEEE Transactions on Information Theory,2007,53(4): 1495-1510.
[7]Shamai S and Sason I.Variations on the Gallager bounds,connections and applications[J].IEEE Transactions on Information Theory,2002,48(12): 3029-3051.
[8]Ma X,Li C,and Bai B.Maximum likelihood decoding analysis of LT codes over AWGN channels[C].The 6th International Symposium on Turbo Codes and Iterative Information Processing(ISTC),Brest,France,Sept.2010:285-288.
[9]IEEE Std 802:16TM-2004.IEEE standard for local and metropolitan area networks part 16: air interface for fixed broadband wireless access systems[S].2004.
[10]3GPP2.C.S0024-B cdma2000 high rate packet data air interface specification[S].2006.
[11]郭琨,黑勇,周玉梅,等.一种应用于不可分层LDPC码的并行分层译码算法[J].电子与信息学报,2010,32(8): 1956-1960.Guo Kun,Hei Yong,Zhou Yu-mei,et al..A parallel layered decoding algorithm for non-layered LDPC codes[J].Journal of Electronics&Information Technology,2010,32(8):1956-1960.
[12]Robertson P,Villebrun E,and Hoeher P.A comparison of optimal and sub-optimal MAP decoding algorithms operating in the log domain[C].IEEE International Conference on Communications(ICC),Seattle,USA,1995:1009-1013.
[13]Sakai T and Shibata K.Fast simulation of LDPC codes over additive non-Gaussian noise channel[C].The 6th International Symposium on Turbo Codes and Iterative Information Processing (ISTC),Brest,France,Sept.2010:216-220.
[14]Zheng X,Lau F C M,and Tse C K.Performance evaluation of irregular low-density parity-check codes at high signalto-noise ratio[J].IET Communications,2011,5(11):1587-1596.
[15]Chen X G and Yang H W.Evaluating the word error rate of channel codes via the squared radius distribution of decision regions[J].IEEE Communications Letters,2008,12(12):891-893.
[16]Wang Z X and Mu Q.A low-complexity layered decoding algorithm for LDPC codes[C].International Forum on Computer Science Technology and Applications(IFCSTA),Chongqing,China,Dec.2009: 318-320.
[17]Dinoi L,Sottile F,and Benedetto S.Design of variable-rate irregular LDPC codes with low error floor[C].IEEE International Conference on Communications(ICC),Seoul,Korea,May 2005: 647-651.
[18]Luo J,Zhang X L,and Yuan D F.Turbo codes with modified code-matched interleaver over AWGN and Rayleigh fading channel[J].Chinese Journal of Aeronautics,2005,18(2):147-152.
[19]Dai L Y and Yang H W.Evaluating word error rate via radius of decision region[C].The 74th IEEE Vehicular Technology Conference (VTC2011-Fall),San Francisco,USA,Sept.2011:1-4.
