改进的TV-Stokes图像修复模型及其算法

许建楼 冯象初 郝 岩

①(西安电子科技大学理学院 西安 710071)

②(河南科技大学数学与统计学院 洛阳 471003)

1 引言

图像修复是当前数字图像处理和计算机图像学中的一个热点问题，其在文物保护、剔除图像或视频中的一些文字、修复网络传输中丢失或损坏的视频信息以及影视特效制作等方面都有很高的应用价值。

从数学的角度看，图像修复是一个病态问题，因为没有足够的信息可以保证能唯一正确地恢复被损坏部分。因此，人们从视觉心理学的角度进行分析，提出了各种假设限定来解决这个问题。

Bertalmio等人[1]首先提出了一种基于等照度线传输的修复模型。该模型依据美术家修复图片的方法，将图片中每个像素点的平滑度沿等照度线传输。由于将图像平滑度填入目标区域，修复后的图像目标区域轮廓自然效果很好。但由于等照度线间无信息交互，为保证模型的稳定性需要强制附加各向异性扩散过程。模型缺乏数学理论依据。Criminisi等人[2]提出了一种基于纹理合成的修复方法。该方法在待修复区域的边界通过块匹配的方式选择合适的纹理进行填充。这种算法虽对纹理修复有较好的结果，但对结构信息的修复能力有限。为了能同时修复结构和纹理，文献[3]提出了一种基于图像分解的非参数采样纹理合成修复方法。在此基础上，Elad等人[4]提出了一种基于图像分解的修复方法，不同的是，他们利用稀疏表示来分别处理获得的结构层和纹理层。这类基于分解的修复算法虽然能较好地修复结构和纹理，但是修复过程比较复杂。对于图像处理问题，小波一直起着举足轻重的作用[5-7]。基于小波的修复技术最先由文献[5]提出。该种方法对于小波系数丢失较少时修复效果较好，但当小波系数丢失较多时，则其修复结果中会出现一些模糊。受文献[5]启发，文献[6]提出了一种基于 Haar小波阈值的修复方法。该方法虽能较好地处理结构信息，尤其是边。但对纹理信息的修复能力有限。

近年来，变分偏微分方程(Partial Differential Equation,PDE)方法已经成为图像处理领域的一种重要工具[8,9]。Chan等人[10]提出了一系列基于变分PDE的图像修复模型。总体变分(Total Variation,TV)模型选择有界变差(Bounded Variation,BV)为图像处理空间，通过对BV空间中的总体变分能量函数求最小值来修复图像。TV模型虽能在噪声情况下有效地对图像进行修复，但不满足人类视觉感知要求的连通性原理。针对这一问题，Chan等人[11]又提出了曲率驱动扩散(Curvature Driven Diffusions,CDD)模型。然而，该模型是一个三阶的PDE，因此数值实现比较复杂。最近，文献[12]基于TV-Stokes方程提出了一个二步修复模型，本文简称为TV-Stokes模型。该模型不仅可以避免高阶导数的计算，而且还能获得较好的修复效果。

本文在研究文献[12]的基础上，提出了一种改进的TV-Stokes修复模型，并利用对偶方法[13]和分裂Bregman方法[14-16]给出一种高效且快速的数值算法。由于新方法对TV- Stokes模型中的两步从构成方式及计算方式上分别进行了改进，因此，数值实验表明，新方法相比于文献[12]不但修复的效果较好，而且修复的速度较快。

2 TV-Stokes模型

最近，文献[12]提出了一个二步图像修复模型(TV-Stokes模型)，该模型经证明对非纹理图像已经取得了较好的修复效果。若记Ω为待修复区域，B为Ω的外围区域，破损图像为d0，修复后的图像为d。则TV-Stokes模型的第1步就是解下面优化问题：

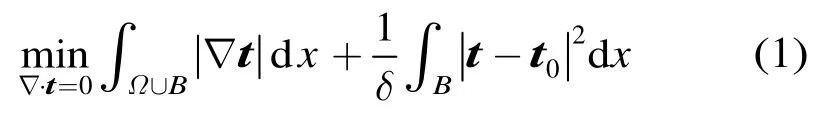
式中t=(θ,v)表示切向量，t0=∇⊥d0表示破损图像的切向量。第1项称为正则项，第2项称为保真项，δ＞0 是正则化参数，它在正则项和保真项之间起着重要的平衡作用。

一旦求得切向量t，则法向量于是TV-Stokes模型的第2步就是重构适合法向量n的图像d。该步通过极小化下面能量泛函来实现

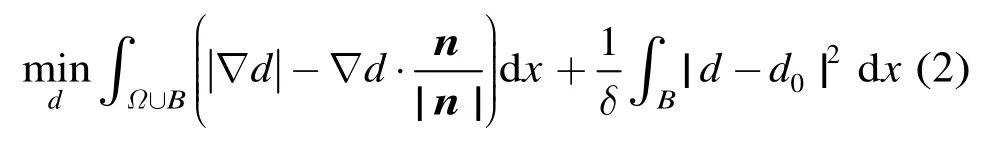
由式(1)看出，TV-Stokes模型在构建切向场t时，仅仅用到了初始的破损图像d0，而没用到第 2步中的重构图d，也就是说，TV-Stokes模型中的两步是独立进行的，并没有相互交织在一起。显然，这样构建的向量场不是很准确。此外，文献[12]用梯度下降法求解上面两步使得算法的修复速度较慢。

3 改进的TV-Stokes模型及算法

3.1 改进的TV-Stokes模型

为了在构建向量场时能够充分利用重构图d的信息，本文提出一个改进的TV-Stokes修复模型。

式中u表示向量场，ω(x)是权函数，前两项是正则项，后两项是保真项，α,β,γ＞0 是正则参数。与TV-Stokes模型一样，本文提出的模型也主要是用于非纹理图像修复。

由于式(3)中包含两个变量u和d，因此可通过交替迭代策略将其转化成下面两个简单的子模型

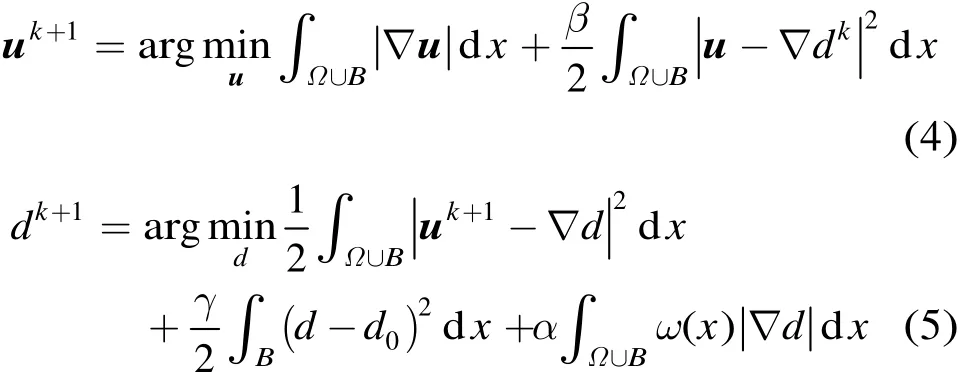
显然，通过式(4)可以构建向量场u，而通过式(5)能够重构与向量场u相适应的图像d，与TV-Stokes模型相比，新模型主要具有以下优点：

(1)式(4)在构建向量场u时，保真项中要求向量场u逼近 ∇dk，充分利用了上层重构出的图像dk，这样可使构建的向量场u更准确。

(2)式(5)在重构图像d时，不仅保真项中充分利用了经式(4)更新过的向量场uk+1，而且模型中还增添了一个加权的TV正则项，该项比不加权的 TV正则项能更好地保持图像的特征[17]。

(3)式(4)，式(5)中的保真项能够随交替迭代不断地进行更新，这一点TV-Stokes模型是无法比拟的。此外，新模型在带噪情况下也能有效地对图像进行修复。

3.2 算法提出

为解式(4)，令u=(u1,u2)，并分别固定u1,u2可得

式(6)，式(7)可以利用Chambolle的对偶方法[13]来求解。与传统的梯度下降法相比，该方法的收敛速度比较快。详见文献[13]。

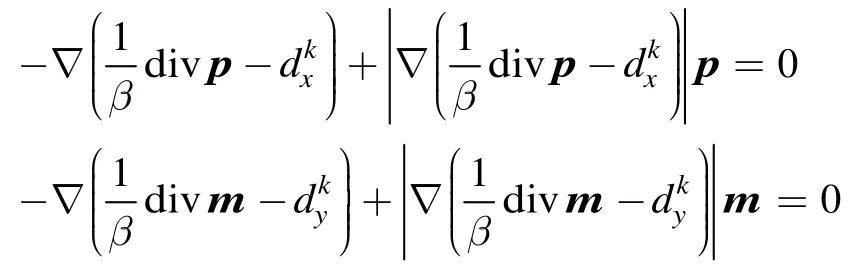
上面两式可以通过固定点迭代来实现。取p0=0,m0=0,则

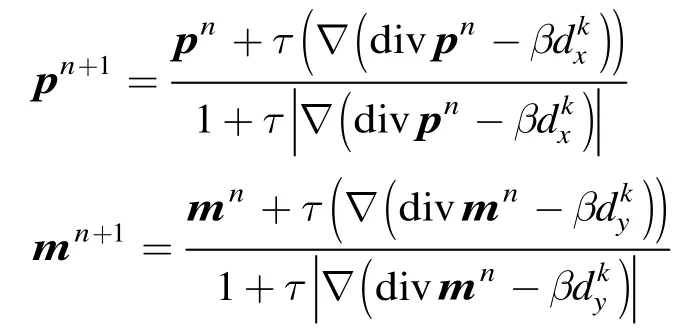
证明 详细推导过程参见文献[13]。

分裂Bregman方法是由文献[14]提出的一种高效的迭代方法，常用于求解带有L1项的优化问题。这种方法具有许多优点。比如编程简单、数值求解过程比较稳定、占有内存小且计算速度和收敛速度快等。但它最主要的优点是收敛速度比较快。详细原因参见文献[14]。本节将采用该方法对式(5)进行数值求解。

首先，在式(5)中引入辅助变量η来处理不可微通过添加等式约束，式(5)等同于下面的新变分问题：

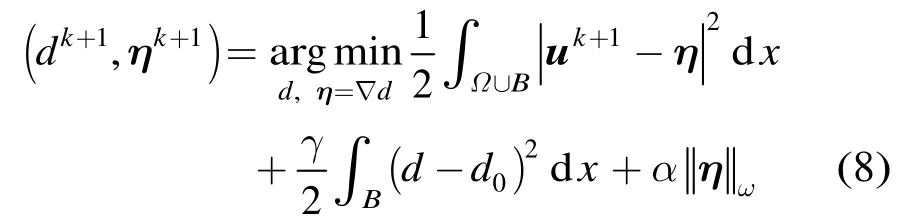
在式(8)中引入惩罚项，使其转化成为无约束问题，并引入Bregman参数b来更新迭代过程。最终，求解式(5)的迭代公式如下：

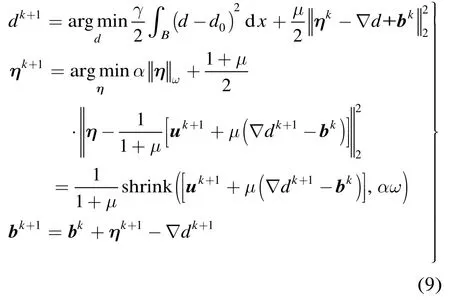
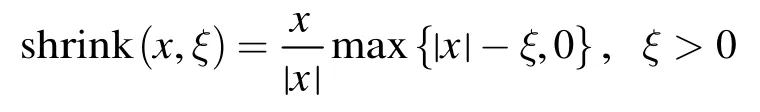
式(9)中第1个问题可由式(10)迭代求得

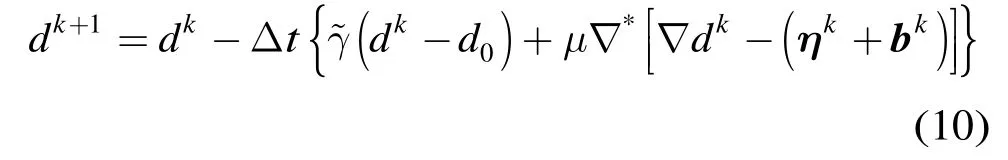
其中 ∇*为梯度算子∇的共轭，

最后，求解式(3)的完整算法描述如下：

步骤 4 停止迭代：对ε＞0 ，当＜ε时，则停止迭代，并输出复原图像；否则，令k=k+ 1，转步骤2。

4 数值实验

为了验证新算法的有效性，本节分别对3幅大小为256×256的受损图像进行修复实验，并将新算法和文献[12]中方法进行比较。为保证比较的客观性和公平性，本文严格按照文献[12]提供的方法对TVStokes模型进行数值实现，并从视觉效果与定量指标两个方面对图像质量进行比较。采用的定量指标为峰值信噪比(Peak Signal to Noise Ratio,PSNR)：

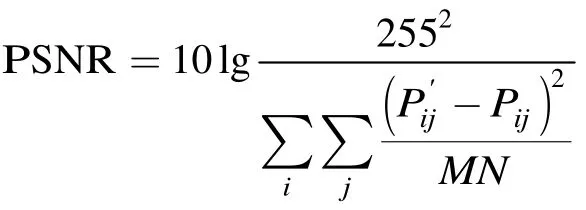
式中P为原始图像，P'为修复后的图像，M和N为图像尺寸大小，i,j为图像像素下标。

文献[12]在做数值模拟时取外围区域B为一个像素宽，为与其保持一致，本文的外围区域B也取成一个像素宽。此外，新模型中权函数ω(x)是一个关于的减函数，本文实验中将其取成1/(1其中c为大于零的常数。新算法步骤 2中内循环次数n取为 2，停止标准中参数ε取成0.01。

实验 1 对含细节丰富的“Lena”图进行修复试验。实验发现，新算法对参数α不是很敏感，对其余参数较为敏感。大量的数值仿真结果表明，参数α在0.001 ～ 5 之间取值时效果较优。本试验中取参数α=0 .1,β=1 /15,μ=0 .35,c=0 .1,Δt=0 .1。图1给出了文献[12]方法和本文方法的修复结果。其中图1(a)为原图像，图1(b)为受损图像，图1(c)和图1(d)分别为文献[12](Δt=0.5)和本文的修复结果。从两种修复结果可以看出，在图1(d)中，Lena的鼻梁比图1(c)得到较好地修复。

图1 Lena图修复结果

实验2 对结构图“House”进行修复实验。实验中参数α取0.09，其余参数取值和实验1中相同。图2给出了两种方法的修复结果。其中图2(a)为原图像，图2(b)为受损图像，图2(c)和图2(d)分别为文献[12](Δt=0.5)和本文的修复结果。比较两种修复结果，可以看出， 在房子左边白色的房檐处，文献[12]方法明显地把灰色扩散进来，引起较大的失真。与其相比，本文方法获得了较好的视觉效果。

实验 3 为了验证新模型在去噪的同时也能对图像进行有效地修复以及权函数ω(x)的有效性，本文还对带噪的受损图“Bird”进行了仿真实验。试验中所用参数分别为α=5,β=0 .5,γ=0 .5,μ=0.5,Δt=0 .2,c=0 .2。图3分别给出了加权和不加权两种情况下的实验结果，其中受损图像中加入了方差为10的高斯白噪声。由图3的结果可以看出，加权的TV正则项比不加权的TV正则项(ω=1)能更好地保持图像的边缘信息与纹理特征，这从小鸟的爪子、翅膀、肚子上的羽毛等都能很清楚地看到。

最后，为了说明新算法的收敛性及其相比于TV-Stokes算法的优越性，本文还在图4中分别绘出了试验1和实验3中峰值信噪比随迭代次数(文献[12]中指第2步的迭代次数)的变化曲线图。从图4(a)曲线的走势可以看出，本文方法不仅修复结果明显优于文献[12]，而且还具有较快的收敛速度。从图4(b)可以看出，加权的修复结果明显优于不加权的结果，并且在两种情况下新算法不但是稳定的，而且还都是收敛的。表1列出了实验1和实验2中两种方法达到停止标准时的实验数据的比较结果。从表中数据可以看出，本文的 PSNR相比于文献[12]有明显提高，修复时间明显少于文献[12]，因此，表1从客观上也表明了本文方法比文献[12]方法不但修复的效果较好，而且修复的速度较快。

5 结论

本文在研究图像修复的基础上，提出了一种改进的TV-Stokes图像修复模型。与文献[12]中模型不同，新模型中仅包含一个能量函数，并且该能量还可以通过交替迭代策略转化为两个相互交织的子模型，由于两子模型的相互交织性，因此它们能随交替迭代相互利用对方的信息，从而使重构的向量场和图像更加准确。为了加快计算速度，在数值计算中分别利用对偶方法和分裂Bregman方法对两个子模型进行交替求解。数值实验表明本文方法比文献[12]中方法不但修复的效果较好，而且修复的速度较快。

图2 House图修复结果

图3 Bird图实验结果

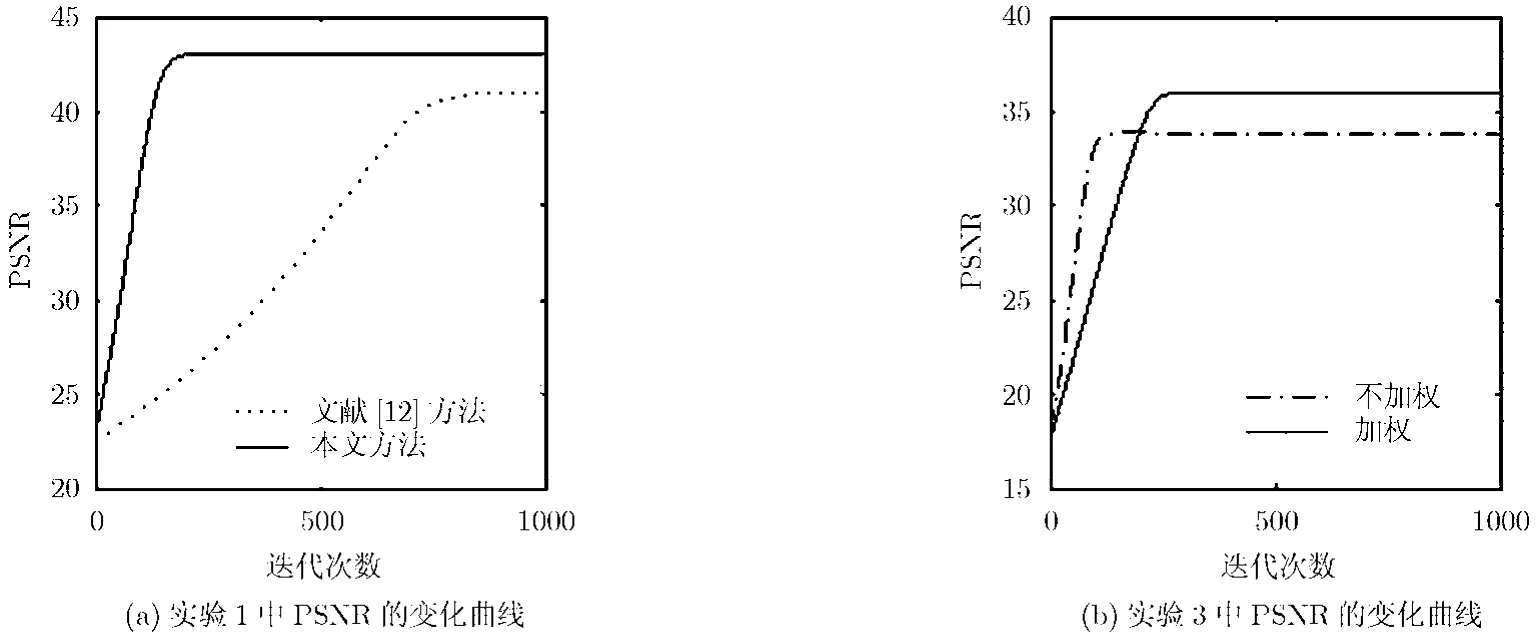
图4 峰值信噪比随迭代次数的变化曲线图

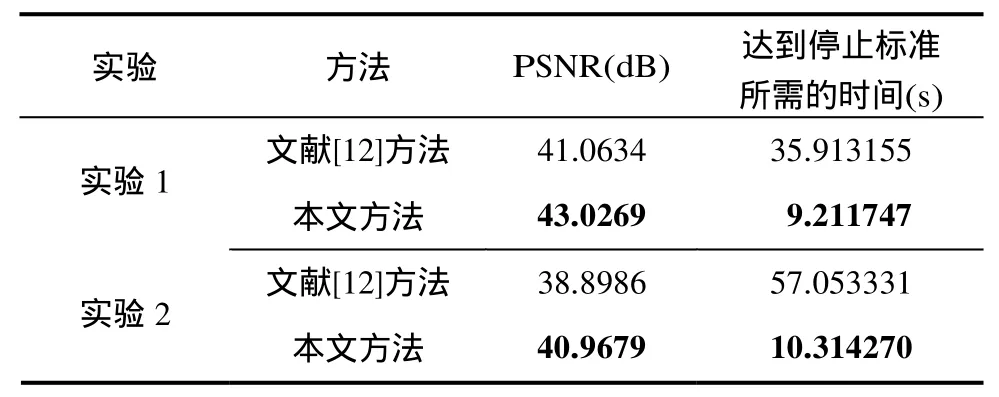
表1 不同方法修复图像迭代达到停止标准时实验数据的对比

[1]Bertalmio M,Sapiro G,Caselles V,et al..Image inpainting[C].Proceedings of the ACM SIGGRAPH,New Orleans,ACM Press,2000: 417-424.

[2]Criminisi A,Pérez P,and Toyama K.Region filling and object removal by exemplar-based image inpainting[J].IEEE Transactions on Image Processing,2004,13(9): 1200-1212.

[3]Bertalmio M,Vese L,Sapiro G,et al..Simultaneous structure and texture image inpainting[J].IEEE Transactions on Image Processing,2003,12(8): 882-889.

[4]Elad M,Starck J,Querre P,et al..Simultaneous cartoon and texture image inpainting using morphological component analysis[J].Applied and Computational Harmonic Analysis,2005,19(3): 340-358.

[5]Chan T,Shen J,and Zhou H.Total variation wavelet inpainting[J].Journal of Mathematical Imaging and Vision,2006,25(1): 107-125.

[6]Chan R H,Setzer S,and Steidl G.Inpainting by flexible haar-wavelet shrinkage[J].SIAM Journal on Imaging Sciences,2008,1(3): 273-293.

[7]You X,Du L,Cheung Y,et al..A blind watermarking scheme using new nontensor product wavelet filter banks[J].IEEE Transactions on Image Processing,2010,19(12): 3271-3284.

[8]张伟斌,冯象初,王卫卫.图像恢复的小波域加速 Landweber迭代阈值方法[J].电子与信息学报,2011,33(2): 342-346.Zhang Wei-bin,Feng Xiang-chu,and Wang Wei-wei.Accelerated Landweber iterative thresholding algorithm in wavelet domain for image restoration[J].Journal of Electronics＆Information Technology,2011,33(2): 342-346.

[9]张军,韦志辉.SAR图像去噪的分数阶多尺度变分PDE模型及自适应算法[J].电子与信息学报,2010,32(7): 1654-1659.Zhang Jun and Wei Zhi-hui.Fractional-order multiscale variation PDE model and adaptive algorithm for SAR image denoising[J].Journal of Electronics＆Information Technology,2010,32(7): 1654-1659.

[10]Chan T and Shen J.Mathematical models of local nontexture inpaintings[J].SIAMJournalonAppliedMathematics,2002,62(3): 1019-1043.

[11]Chan T and Shen J.Non-texture inpainting by curvature driven diffusions (CDD)[J].Visual Communication and Image Representation,2001,12(4): 436-449.

[12]Tai X C,Osher S,and Holm R.Image Inpainting Using a TV-Stokes Equation[M].Heidelberg,Germany,Springer,2007: 3-22.

[13]Chambolle A.An algorithm for total variation minimization and applications[J].Journal of Mathematical Imaging and Vision,2004,20(1/2),89-97.

[14]Goldstein T and Osher S.The split Bregman method for L1 regularized problems[J].SIAM Journal on Imaging Sciences,2009,2(2): 323-343.

[15]Wu C L and Tai X C.Augmented Lagrangian method,dual methods and split-Bregman iterations for ROF,vectorial TV and higher order models[J].SIAM Journal on Imaging Sciences,2010,3(3): 300-339.

[16]Goldstein T,Bresson X,and Osher S.Geometric applications of the split Bregman method: segmentation and surface reconstruction[J].Journal of Scientific Computing,2010,45(1-3): 272-293.

[17]陈利霞,冯象初,王卫卫,等.加权变分的图像去噪算法[J].系统工程与电子技术,2010,32(2): 392-395.Chen Li-xia,Feng Xiang-chu,Wang Wei-wei,et al..Image denoising algorithms based on weighted variation[J].Systems Engineering and Electronics,2010,32(2): 392-395.