迭代对角加载采样矩阵求逆鲁棒自适应波束形成

金 伟 贾维敏 姚敏立

(第二炮兵工程大学 西安 710025)

1 引言

波束形成广泛应用于雷达、声纳、射电天文、地震学、通信和医疗成像等领域[1]。经典的 Capon波束形成器，具有良好的分辨率和干扰抑制能力，是自适应波束形成器的典型代表，但需要准确的期望信号导向矢量[2]。然而，在实际中，由于期望信号的假设到达角与实际到达角有误差，或者阵列响应的假定值与真实值有误差(阵列校正误差)等原因，假设的期望导向矢量可能不完全准确，与真实值之间有失配误差，从而导致Capon波束形成器的性能急剧下降，甚至比常规波束形成器更差。因此，如何增强Capon波束形成器的鲁棒性成为阵列传感器应用系统一个亟待解决的问题。

近三十年来，学者们提出多种算法来改善Capon波束形成器的鲁棒性。传统的方法主要有线性约束最小方差(LCMV)方法、对角加载方法、特征子空间方法和协方差矩阵消锥(CMT)方法等[3]。前述方法只是针对某一种失配误差有效或者只在较高信噪比(Signal to Noise Ratio,SNR)时有效，都没有与具体的失配误差建立起联系，因此均具有一定的局限性。虽然对角加载算法对一般性的误差具有一定的鲁棒性，但其加载因子难以选择[4]。

近些年，涌现出了一类具有明确理论背景的鲁棒波束形成算法，最坏性能最优法(Worst-Case,WC)[5]，鲁棒 Capon波束法(Robust Capon Beamformer,RCB)[6]是其典型代表，它们均属于基于不确定集理论的鲁棒波束形成算法。该类算法通过对导向矢量的失配误差进行建模，将其限定在球体或椭球体内，并将约束优化问题转化为凸优化问题，或对最优加载量的数值求解问题。理论推导分析证明这两种算法都可归为对角加载算法的范畴[6]。自从基于不确定集类的鲁棒波束形成算法提出后，关于鲁棒波束形成的研究着重集中在对不确定集类算法的深入研究和推广应用[7-10]上。这些方法通过凸优化或者支持向量机方法对约束优化问题进行求解，算法相对比较复杂。

当 DOA偏差比较大时，基于不确定集的鲁棒波束形成器性能下降。针对这一问题，Nai等人[11]提出了迭代鲁棒最小方差法(Iterative Robust Minimum Variance Beamforming,IRMVB)，采用较小的不确定集，运用RCB算法对期望导向矢量进行迭代求解，能够求解出更为准确的期望导向矢量。该文献利用最优化问题中的敏感度分析理论[12]以及对期望信号的 DOA进行区间限制，设计了迭代算法的终止条件。Lie等人[13]在此基础上，提出一种自适应不确定集迭代算法(Adaptive Uncertainty based Iterative RCB,AU-IRCB)，对每次迭代所用的不确定集大小进行自适应地调整，加快了收敛速度。然而，这两种方法仍然是基于不确定集思想发展起来的，属于对不确定集方法的改进算法。

针对导向矢量失配误差较大的情况，本文从一个新的角度出发，提出了一种迭代对角加载采样矩阵求逆(ILSMI)鲁棒自适应波束形成算法。该算法利用Capon波束形成器的最优权矢量与假定导向矢量的基本关系，对传统对角加载算法进行迭代计算，从而得出较为准确的期望信号导向矢量。算法能够明显提高导向矢量大失配误差情况下的阵列输出SINR，并且不需要对导向矢量建立不确定集约束，避免了在每次迭代中运用拉格朗日法或凸优化方法对问题进行求解。

2 问题描述

一个线性阵列窄带波束形成器的输出通常可表示为

式中w=[w1,w2,…,wM]T为自适应阵列加权矢量，M为阵元个数，x(k)为M×1维阵列接收数据矢量，y(k)为阵列输出，k为采样时刻，(⋅)T表示转置，(⋅)H表示共轭转置。

接收数据矢量x(k)可表示为

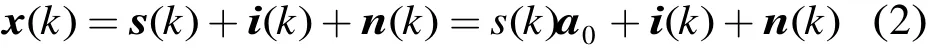
其中s(k),i(k),n(k)分别为期望信号、干扰信号和高斯白噪声分量，s(k)为期望信号波形，a0为期望信号对应的导向矢量。

2.1 Capon波束形成器

Capon波束形成器是自适应波束形成器的典型代表，可表示为

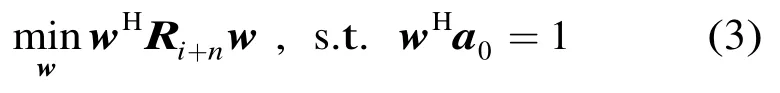
式中Ri+n表示干扰加噪声协方差矩阵。在实际应用中，Ri+n难以得到，一般都用阵列输出的采样协方差矩阵代替，假设快拍数为N，则

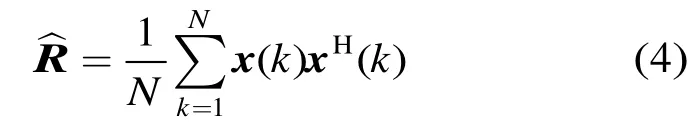
此时的Capon波束形成算法称为采样矩阵求逆算法(Sample Matrix Inversion,SMI)，其最优权矢量为

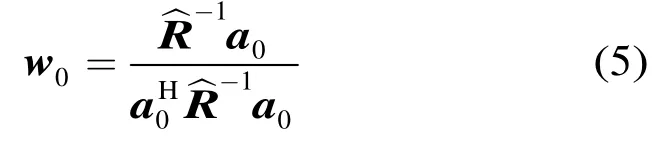
2.2 对角加载

Capon波束形成器需要准确的期望信号导向矢量a0。然而在实际中，这一信息通常不能精确获得，一般以假设值代替，与真实值a0之间往往有一定的失配误差，有可能造成Capon波束形成器在真实的信号方向形成零陷，性能大大降低，因此需要研究能克服导向矢量失配误差影响的鲁棒波束形成技术。

对角加载算法LSMI是一种常用的鲁棒波束形成算法，近年来提出的具有完善理论背景的不确定集类算法大都被证明是广义对加载方法[6]，这进一步说明了LSMI算法应用的广泛性。基本的LSMI算法就是在信号协方差矩阵上引入一个对角矩阵，即解决如下优化问题：

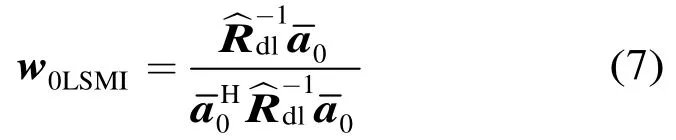
通过引入对角加载矩阵，LSMI算法对噪声子空间的扰动具有一定的抑制能力，从而在一定程度上提高了波束形成器的鲁棒性。该算法的关键问题就是加载因子λ难以选择，其中一个经验值取法就是λ等于10倍的噪声功率[4]。但是，这种参数选择方法具有很大的随意性，其效果也有限。

RCB等不确定集类鲁棒波束形成方法，之所以能取得比LSMI更优的性能，在于它们能够求出一个在一定意义上最优的对角加载因子λ。然而，当导向矢量失配误差较大时，RCB的输出SINR下降。这是因为为了克服大的导向矢量失配，RCB此时也要相应地采用大的不确定集，以保证真实的期望信号导向矢量能够包含在以假定导向矢量为中心的不确定集中。这种大的不确定集削弱了波束形成器对干扰信号的抑制能力，从而降低了阵列的输出SINR[11,13]。在这一问题背景下，IRMVB算法考虑使用小的不确定集，进行多次迭代，用每次迭代得到的信号导向矢量代替假设值，从而更为准确地逼近真实的期望信号导向矢量[11]。IRMVB方法仍然基于不确定集理论，但是它却不再属于对角加载的范畴[13]。

3 迭代对角加载鲁棒自适应波束形成算法

当前关于鲁棒自适应波束形成的研究主要集中在对不确定集方法的改进与推广应用上，很少有针对LSMI算法本身来进行深入研究的。本文从最基本的LSMI出发，通过提出的迭代对角加载采样矩阵求逆(ILSMI)鲁棒自适应波束形成算法估计出较准确的期望导向矢量，从而提高了算法对导向矢量大失配误差的鲁棒性。

3.1 算法提出

当真实的导向矢量a0不能准确知道，只能以假设值a0代替时，式(5)中的SMI算法权矢量为

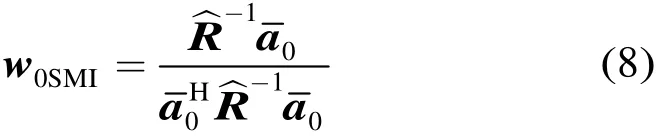
观察式(8)可以发现，权矢量与期望导向矢量存在一定关系，图1给出了这种Capon波束形成器的最优权矢量与导向矢量的对应关系示意图。

如果假定的导向矢量a0比较准确，那么用SMI算法求解的权矢量就比较合适，输出 SINR就比较高，当假定导向矢量a0完全等于真实值时，此时式(8)就等同于标准Capon波束形成器；反之，如果导向矢量不准确，存在一定的失配误差，那么求取的权矢量就不合适，对SMI算法来说，就有可能会在期望信号方向形成零陷，降低输出SINR。

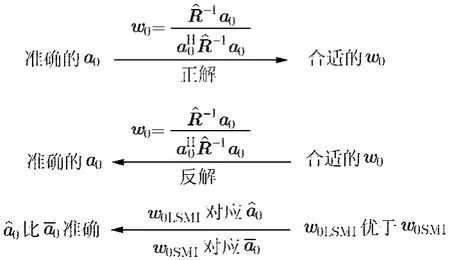
图1 最优权矢量与导向矢量关系

前面的分析考虑了导向矢量假设值的准确与否对求解的波束形成器权矢量的影响，反之，如果能够得到一个合适的权矢量，那么按照式(5)的关系，将可以对应反解出一个较准确的导向矢量，如图1所示。

LSMI方法通过引入对角加载因子，改善了波束形成器的鲁棒性。尽管这种改善不一定达到最优，但是可以认为，通过LSMI求解得到的权矢量式(7)要比不引入对角加载因子的SMI得到的权矢量式(8)更为合适。

当不引入加载因子时，按照式(8)计算出的权矢量w0SMI与假定导向矢量对应。如果将引入了对角加载因子的 LSMI算法计算得到的权矢量w0LSMI代入式(5)，将可对应反解出期望信号导向矢量估计值。由于权矢量w0LSMI比w0SMI更为合适，那么如图1所示，运用Capon波束形成器矢量与导向矢量的关系进行反解，即可以认为比更为准确，更接近真实的期望导向矢量。

如果以这个更为准确的导向矢量估计值替换掉假定的导向矢量，再次运用LSMI算法求取权矢量，并依照图1进行反解，将会得到一个相对更加准确的期望导向矢量。如此迭代下去，最终将逼近真实的期望导向矢量。

3.2 期望信号导向矢量估计与终止条件设计

下面具体讨论如何对期望导向矢量进行估计以及如何设计迭代算法的终止条件。按上面分析，可将式(7)与式(5)进行联立求解w0LSMI对应的由此得

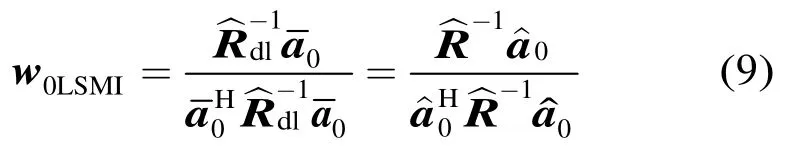
由于α1是的二次函数，式(10)是的二次方程式，要通过式(10)求解比较困难。然而，考虑到导向矢量的模是恒定值(且α0和α1都是比例因子，我们可以通过对aˆ0去比例因子后再进行范数归一化的方法进行求解，即

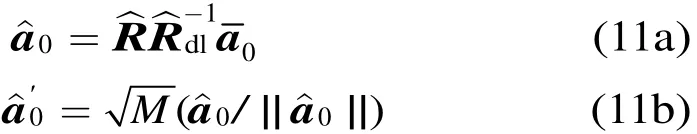
ILSMI算法采用与IRMVB算法相类似的终止条件。根据最优化问题中的敏感度分析理论[12]，文献[11]设计了第1个终止条件，即当拉格朗日乘子小到一定程度，对最优值的影响非常小时，程序中止。本文的ILSMI算法避开了拉格朗日乘子的求解，因此只需要对前后两次迭代得到的导向矢量之间的差值进行约束，即式(12a)所示。ILSMI的第2个终止条件与文献[11]相同，即：在低SNR时，迭代算法有可能收敛至干扰对应的导向矢量，从而导致输出SINR很低，为避免这一问题，假定期望信号DOA波束主瓣宽度)区域内，则算法的第 2个终止条件可设为(12b)。

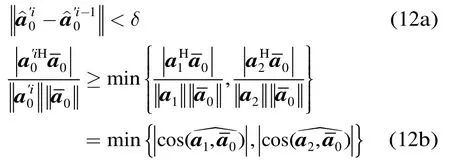
其中δ为一约束参数，a1和a2分别为-Δθ和+ Δθ对应的导向矢量，表示两矢量夹角的余弦运算。当迭代算法满足这两个终止条件中的任意一个时，算法中止。

3.3 算法流程

ILSMI算法流程总结如下：

(1)初始化：i=0时，=；

(2)当i≥1时，通过式(11a)(用替换)计算并通过式(11b)对进行范数归一化，得到；

(3)判断式(12)的终止条件是否满足，如果任一条件满足，转到步骤(4)，算法终止，否则转到步骤(2)；

(4)使用收敛的导向矢量估计值代替式(5)中的a0计算权值。

图2描述了ILSMI算法对期望导向矢量不断更新和约束的过程。

图2 ILSMI算法示意图

4 实验仿真及结果分析

假设阵列为间隔半波长的均匀线阵，阵元数为10，均为全向阵元。加载的噪声为零均值、单位方差的空间高斯白噪声。期望信号真实方向为6°，假设方向为0°。两个干扰信号分别从20°和30°入射，功率均为 30 dB。期望信号与干扰、干扰信号之间均相互独立。假设期望信号的来波方向位于区间[- 7°,+ 7°]之内，即Δθ=7°。实验对采样矩阵求逆算法(SMI)、对角加载算法(LSMI)、鲁棒Capon波束形成算法(RCB)和本文提出的迭代对角加载采样矩阵求逆鲁棒自适应波束形成算法(ILSMI)进行比较。RCB的不确定集参数取为该仿真条件下的最优值ε1=8.5,ILSMI方法终止条件式(12a)中的参数取为δ=0 .01,LSMI 和ILSMI的对角加载因子均为λ=1 0(由于实验中加载的噪声功率为单位1，因此在实验中λ均取10(除实验4外))。实验结果来自100次独立的蒙特卡罗实验。

实验1 方向图比较 取快拍数为100,SNR=0 dB，几种算法的归一化方向图如图3所示。

从图3可以看出，SMI算法鲁棒性最差，在真实的期望信号方向形成了零陷。LSMI和RCB虽然对失配误差有一定的鲁棒性，但其波束图主瓣却指向假定的期望信号方向，在真实的期望信号方向上性能有所下降。ILSMI算法的主瓣指向了真实的期望信号方向，对失配误差具有很强的鲁棒性，并且ILSMI算法的旁瓣电平明显地比其它几种算法要低。

实验2 不同输入SNR下的输出SINR比较

在快拍数为100,SNR较低的情况下，几种算法的输出SINR随输入SNR变化的关系图如图4所示。从图中可以看出，SMI对大的导向矢量失配误差基本不具有鲁棒性，LSMI算法虽然具有一定的鲁棒性，但随着 SNR的增加，其性能开始下降。RCB算法本身的鲁棒性比LSMI好，这是由于RCB算法求得了一个在一定程度上比LSMI所用加载因子更优的加载量，而ILSMI算法的输出SINR则明显地要高于其它几种算法，说明在低 SNR情况下，用ILSMI进行迭代求解的期望导向矢量估计值更加逼近真实值。

实验 3 不同快拍下的输出 SINR 比较 取SNR=0 dB，考查几种算法的输出SINR与快拍数之间的关系，其结果如图5所示。

从图5可以看出，随着快拍数的增加，几种算法的输出 SINR渐趋恒定。其中 SMI算法的输出SINR随快拍数增加反而下降，对大的导向矢量失配误差不具备鲁棒性。LSMI和RCB算法输出SINR随快拍数增加而增加，但是增加幅度有限，表明对较大的导向矢量失配误差具有一定的鲁棒性。ILSMI效果最好，其稳态值比RCB高4 dB左右，与理论最优值相差0.6 dB左右，这进一步说明了在低SNR情况下，用ILSMI算法可以迭代求解出较为准确的期望导向矢量，从而可以获得近似最优的权矢量。

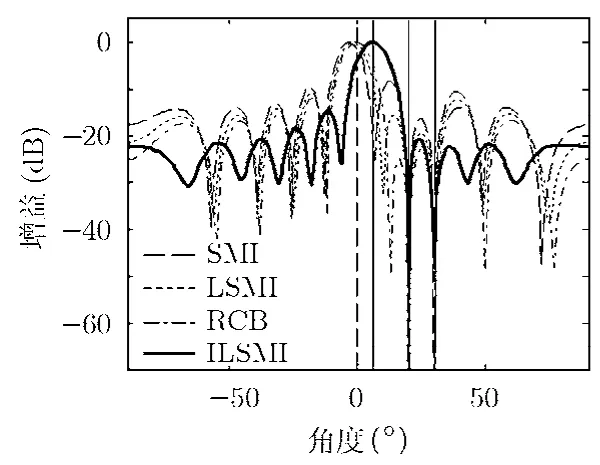
图3 归一化方向图

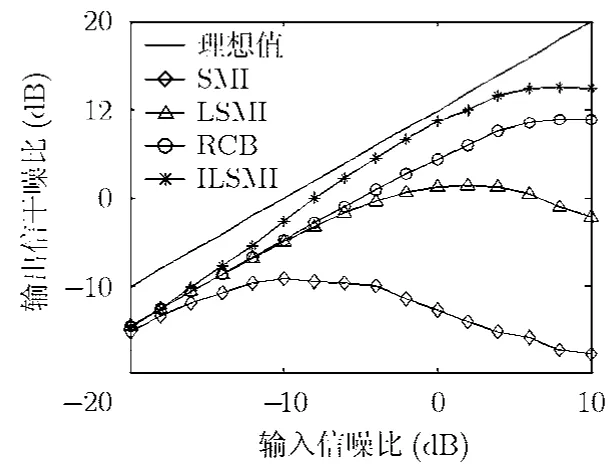
图4 SINR与SNR关系

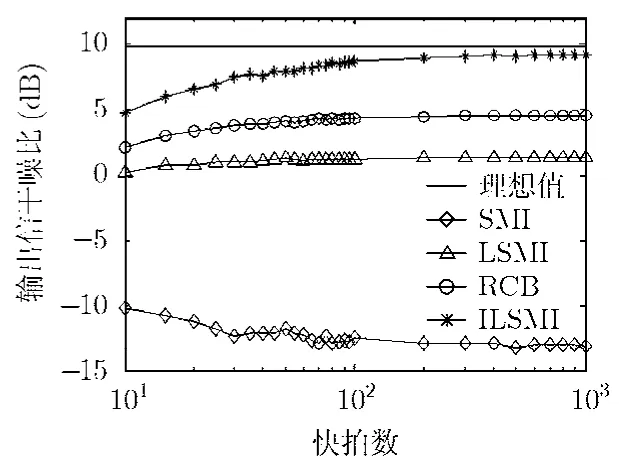
图5 SINR与快拍数关系

实验4 不同参数下的收敛速度比较 取SNR=-5 dB，考察ILSMI在不同加载因子情况下的输出SINR随迭代次数的变化，并与文献[11]中的IRMVB方法(其不确定集参数取文献[11]中的ε2=0.1)进行比较，其结果如图6所示。为方便比较，仿真采用了理想的阵列输出协方差矩阵，图中几条曲线均是在未施加终止条件下得出的，每种情况下应该进行终止的次数在图中已由不同符号标记出来。从图中可以看出，ILSMI算法比IRMVB算法所需迭代次数少，收敛速度快。随着迭代次数的增加，ILSMI算法的SINR会逐渐增加，直到程序中止，如果不对ILSMI算法施加终止条件，则SINR会随着迭代次数的继续增加而逐步下降，这说明了ILSMI算法的终止条件必不可少。另外，从图中还可以看出，加载因子λ是影响ILSMI算法的重要因素，加载因子越小，收敛越慢，加载因子越大，收敛越快。为了与传统对角加载算法加载因子取 10倍噪声功率相一致[4]，从而保证算法比较的客观和公正，我们在实验1-实验3中均采用了λ=10。

以上几个实验反映了ILSMI算法在低SNR时表现出了良好的性能。然而，与现有大部分鲁棒波束形成方法一样，ILSMI算法在SNR较高时性能会有所下降，这有待下一步研究。

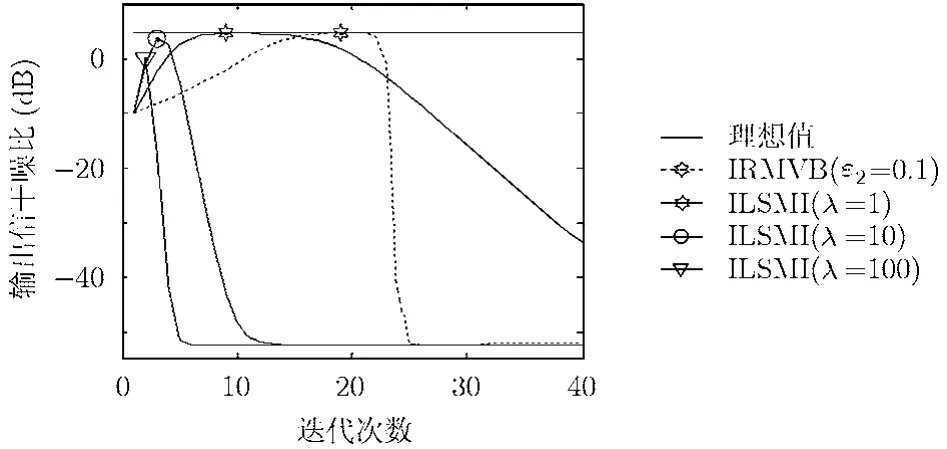
图6 SINR与迭代次数关系

5 结论

当导向矢量失配误差较大时，不确定集类鲁棒波束形成方法性能下降。为有效克服较大的导向矢量失配误差，本文从一个新的角度出发，提出了一种迭代对角加载鲁棒自适应波束形成算法 ILSMI。该算法不需要对导向矢量建立不确定集限制，避免了在每步迭代中运用凸优化方法或拉格朗日乘子法。算法只需一步关键递推关系式，就可迭代求解出较准确的信号导向矢量，算法简单，且能够明显提高波束形成器在低SNR情况下的输出SINR。这表明在大的导向矢量失配误差下，即使不对导向矢量进行不确定球集(或椭球集)限制，只要通过对最基本的LSMI算法进行有效处理，仍然可以提高输出SINR，甚至高于文中所比较的不确定集类方法。

[1]Van Trees H L.Optimum Array Processing[M].New York:USA,Wiley Press,2002: 1-12.

[2]Capon J.High-resolution frequency-wavenumber spectrum analysis[J].Proceedings of the IEEE,1969,57(8): 1408-1418.

[3]Li Jian and Stoica P.Robust Adaptive Beamforming[M].New Jersey,USA: Wiley,2005: 49-60.

[4]Carlson B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Transactions on Aerospace and Electronic Systems,1988,24(4): 397-401.

[5]Vorobyov S A,Gershman A B,and Luo Zhi-quan.Robust adaptive beamforming using worst-case performance optimization: a solution to the signal mismatch problem[J].IEEE Transactions on Signal Processing,2003,51(2):313-324.

[6]Li Jian,Stoica P,and Wang Zhi-song.On robust Capon beamforming and diagonal loading[J].IEEE Transactions on Signal Processing,2003,51(7): 1702-1715.

[7]Nai S E,Ser W,Yu Zhu-liang,et al..A robust adaptive beamforming framework with beampattern shaping constraints[J].IEEE Transactions on Antennas and Propagation,2009,57(7): 2198-2203.

[8]Lei Lei,Lie J P,Gershman A B,et al..Robust adaptive beamforming in partly calibrated sparse sensor arrays[J].IEEE Transactions on Signal Processing,2010,58(3):1661-1667.

[9]Hassanien A,Vorobyov S A,and Wong K M.Robust adaptive beamforming using sequential quadratic programming: an iterative solution to the mismatch problem[J].IEEE Signal Processing Letters,2008,15(11): 733-736.

[10]Lu Yao,An Jian-ping,and Bu Xiang-yuan.Adaptive bayesian beamforming with sidelobe constraint[J].IEEE Communications Letters,2010,14(5): 369-371.

[11]Nai S E,Ser W,Yu Zhu-liang,et al..Iterative robust minimum variance beamforming[J].IEEE Transactions on Signal Processing,2011,59(4): 1601-1611.

[12]Boyd S and Vandenberghe L.Convex Optimization[M].Cambridge,UK,Cambridge University Press,2004: 249-272.

[13]Lie J P,Ser W,and See C M S.Adaptive uncertainty based iterative robust Capon beamformer using steering vector mismatch estimation[J].IEEE Transactions on Signal Processing,2011,59(9): 4483-4488.