平地无风条件下红松针叶床层林火蔓延的影响因子分析及模拟1)

金 森 褚腾飞 邸雪颖 刘礴霏 张吉利

(东北林业大学，哈尔滨，150040)

火行为是指林火发生发展过程中所表现出来的各种特征的总和，包括林火蔓延速度、火焰高度、驻留时间、反应区宽度、可燃物消耗量和林火强度等指标［1］。了解、掌握可燃物的林火行为，是做好森林火险预报、提高森林火灾扑救效率和更好地分析、理解林火对森林生态系统影响的基础［2］。火行为受可燃物组成和理化性质、可燃物床层特征及环境因素的影响，复杂性高。以火行为模型为主要任务的林火行为研究是林火科学的重要研究领域，国内开展得也相当广泛［3－9］。火行为模型一般可分为物理、半物理和实验统计模型3类［10］。物理模型普适性好，但要求较高的计算能力，在目前的技术条件下，还难以广泛应用［10］。在实际中得到广泛应用的都是在很大程度上或完全依赖于点烧试验的半物理模型和实验统计模型，如Rothermel模型［11］、加拿大火行为模型［12－14］、澳大利亚火行为模型［15－16］。这些半物理模型和实验统计模型，特别是后者，因使用很多来自点烧试验的方程和参数，对计算能力的要求不高，从而得到广泛的应用，但也恰恰是因为对试验条件依赖大，影响了这些模型的推广使用。在目前的经济技术条件下，对于一个地区而言，如果建立至少适用于该区域的试验统计火行为模型或半物理火行为模型，必须对该区域内的主要可燃物类型的火行为进行系统研究，了解、掌握它们在不同可燃物床层条件和环境条件下的火行为特征。

红松(Pinus koraiensis)针阔混交林是温带森林生态系统的顶级群落，这些林下的可燃物由不同的针叶、阔叶组成，其火行为受这些组分的火行为影响［11，17］。了解、掌握这些组分的火行为，对于建立更准确的混合可燃物模型十分必要。为此，笔者对该林分下的主要可燃物的组分进行了实验室点烧试验，分析影响其火行为的主要因子。这些影响因子往往因可燃物组分的不同而有所变化［17］，需分别研究，然后才能建立相应组分的火行为预测模型。为此，本文给出了红松针叶床层的室内点烧试验中有关林火蔓延速率研究的初步结果，其目的是:给出平地无风条件下红松针叶床层的蔓延速率的基本数据;确定影响红松针叶床层蔓延速率的主要因子，以及这些因子对林火蔓延速率的影响之间是否相关;建立红松针叶床层的林火蔓延速率模型。

1 研究方法

1.1 试验材料采集

红松松针采于东北林业大学帽儿山试验林场老山(127°30'～127°34'E，45°20'～45°25'N)红松(Pinus koraiensis)人工林。林场所处地域属温带大陆性气候。年平均气温2.8℃;1月份最冷，气温日变化范围在－18～－23℃;7月份最热，气温日变化范围在21～22℃。年平均降水量723.8 mm，雨水集中在6—8月份。林分树龄50 a，林分平均胸径21.1 cm，平均树高13.4 m。林下植被以毛榛子(Corylus mandshurica)、刺五加(Acanthopanax senticosus)、东北山梅花(Philadelphus schrenkii)、苔草(Carex sp.)为主。地表可燃物主要是凋落的红松针叶，混有少量的阔叶落叶。

1.2 室内点烧试验

点烧试验在东北林业大学帽儿山森林防火实验室内进行。2010年春季，在研究地区的红松林下进行红松针叶采集，同时测定可燃物的载量、厚度等特征，在实验室内模拟这些可燃物的野外条件，铺设不同含水率、载量和高度组合的均匀的红松针叶床层。其中可燃物含水率设5个水平:5%、10%、15%、20%、25%。载量设 5 个水平:4 、5、6、7、8 t·hm－2。可燃物床层高度设4个水平:3、5、7、9 cm。共铺设5×5×4=100个不同的3因素交叉水平床层，进行了100次点烧试验。可燃物含水率采用如下方法调制:先将可燃物均匀浸湿，然后将其分层放置在自制的大烘箱内(3.2 m×1.9 m×2.3 m)，控制温度进行烘干，使含水率逐渐下降，采用高精度快速水分测定仪AND—ML50测定含水率，直到可燃物含水率达到设定的水平。根据预定的可燃物含水率和载量，计算出每次点烧所需可燃物的鲜质量，然后称量同样质量的可燃物进行铺设。燃烧床的尺寸为2 m×2 m。燃烧床水平放置，模拟平地无风条件下的燃烧。在燃烧床一端固定有一点火槽，放入乙醇后点燃，可迅速形成一条火线。每次点烧点燃后，火头呈一条直线向前蔓延。当火蔓延达到“似稳态”(Quasisteady state)时开始记录燃烧时间及火焰高度，采用标杆法测量林火蔓延速率［18－20］，用摄像机在燃烧床正面及侧面同时记录点烧过程。

1.3 数据分析

1.3.1 红松针叶床层林火蔓延速率的基本特征

通过对100次点烧试验的统计分析，给出红松针叶床层平地无风条件下林火蔓延速率的基本特征，如均值、中数、最大、最小值等。

1.3.2 红松针叶床层林火蔓延速率的影响因子分析

研究［21］表明，影响林火蔓延的因子间存在一定的交互作用。一些因子对林火蔓延的影响往往被其他因子的作用所掩盖。只有在保持其他因子不变而只有目的因子变化时，才能准确揭示目的因子对林火的作用。因此，文中的分析包括两个方面:一是全部点烧数据放在一起，即各因子都在变化时，分析某一因子对可燃物蔓延速率的影响，以判断该因子对蔓延速率影响的强度;另一个是其他因子不变时，单独剥离出该因子的作用。对两者进行比较，以分析该因子的影响与其他因子间的交互关系。

1.3.2.1 含水率对林火蔓延速率的影响

用全部点烧数据绘制红松针叶含水率和林火蔓延速率的散点图，并计算其相关系数。然后以载量(5个水平)和高度(4个水平)为分类变量，将100次点烧试验数据分为5×4=20组，每组点烧试验的可燃物床层的载量和高度相同而含水率不同，以揭示含水率对蔓延速率的独立影响。分别绘制这20组数据的红松针叶含水率和林火蔓延速率的散点图，并计算其相关系数。比较分类数据的散点图和全部数据的散点图所表现出来的含水率和蔓延速率之间的关系，分析红松针叶含水率对林火蔓延速率的影响及这种影响与针叶床层载量和高度的关系。

1.3.2.2 床层载量对林火蔓延速率的影响

与1.3.2.1同法，只是采用红松针叶含水率(5个水平)和床层高度(4个水平)作为分类变量进行数据分组，共20组分类数据。

1.3.2.3 床层高度对林火蔓延速率的影响

与1.3.2.1同法，只是采用红松针叶含水率(5个水平)和床层载量(5个水平)作为分类变量进行分组，共25组分类数据。

1.3.2.4 床层压缩比对林火蔓延速率的影响

可燃物床层压缩比对林火蔓延速率有影响，但压缩比与可燃物床层载量和高度是联系在一起的，在试验中无法单独剥离处理。在1.3.2.2和1.3.2.3中，红松针叶床层载量和高度对蔓延速率的影响分析中就隐含着压缩比对林火蔓延速率的影响，且两者的趋势是一致的。为此，只用全部点烧试验数据绘制可燃物床层压缩比和林火蔓延速率的散点图，并计算相关系数，以综合分析压缩比对林火蔓延速率的影响。压缩比采用计算公式为:β=L/(Dρp)。式中:β为压缩比;ρp为可燃物颗粒密度(g·cm－3)，试验测定;L为床层载量(g·cm－2);D为床层高度(cm)。

1.3.3 建立红松针叶床层林火蔓延速率的预测模型

式中:xi为第i个建模因子;fi为因子xi对林火蔓延速率的影响函数;n为所采用的建模因子数量。

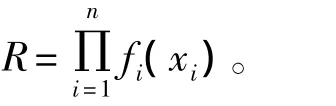
本文的加式模型采用线性回归形式，要求各因子之间不能存在强烈的相关，因此，载量和压缩比、高度和压缩比不能同时出现在加式模型中。同时要考虑各因子之间的交互作用，若交互作用显著，则将其加入模型中。对于所有的加式和乘式模型，都进行100次的交叉验证，即每次选择1次点烧数据作为验证数据，用其余99次点烧数据建模。计算这100次验证的平均绝对误差(EM，A)和平均相对误差(EM，R)。误差的计算公式为:

式中:Ri和Ri'分别为实测和预测的红松针叶床层的林火蔓延速率(m·min－1)。

2 结果与分析

2.1 红松针叶床层林火蔓延速率的特征

表1给出了100次点烧试验的基本情况。其中红松针叶床层的林火蔓延速率为0～0.399 m·min－1，平均值为0.2 m·min－1。从 75%的区间值看，多数红松针叶点烧试验的林火蔓延速率小于0.3m·min－1。红松针叶床层的压缩比从 0.014 到 0.084。在100次点烧试验中，有9次没有持续燃烧，其中6次试验的红松针叶含水率为25%，其余3次的含水率为20%。

2.2 红松针叶床层林火蔓延速率的影响因子

2.2.1 可燃物含水率的影响

图1给出了用100次点烧试验数据绘制的红松针叶床层林火蔓延速率和含水率之间的关系。从图1中可见，含水率对红松针叶床层林火蔓延速率具有显著的阻滞作用。图2给出了相同载量和高度时红松针叶床层含水率与林火蔓延速率之间的关系，其中各小图的拟合直线的斜率比较相似，表明红松针叶床层林火蔓延速率和含水率之间的关系在不同的载量和高度的红松针叶床层间是一致的，说明红松针叶含水率对林火蔓延速率的影响与红松针叶床层的载量、高度无明显关系。图2中各小图的压缩比不同，这也说明红松针叶含水率对林火蔓延速率的影响独立于床层压缩比，这在2.3的建模过程中得到了验证。图1和图2的比较研究表明，红松针叶含水率对红松针叶床层林火蔓延速率的影响在其他床层特征一致和混合床层特征两个条件下是一致的，即都表现为较强的线性关系。

表1 点烧试验和蔓延速率的统计数据(样本数为100)

图1 林火蔓延速率与可燃物含水率之间的关系(全部100次点烧试验数据)

在本文的研究中，可燃物含水率对林火蔓延速率的影响是线性的，这与 Burrows［22］和 Baeza［23］的点烧试验结果相似。在Rothermel模型［11］中，可燃物含水率对林火蔓延速率的影响是用含水率的三次多项式和一次多项式的商来表示的，其他研究则用幂函数［12，16］或指数函数［24，15］来描述，与本文所得结果不同。

2.2.2 红松针叶床层载量的影响

从图3中可见，红松针叶层载量对林火蔓延速率具有非常弱的影响，随载量的增加，红松针叶床层的林火蔓延速率略有增加，但未达到0.05的统计显著水平。图4给出了相同床层高度和含水率时载量与红松针叶床层林火蔓延速率之间的关系，其中各小图所表现出的床层载量与林火蔓延速率之间的关系比较复杂，在20个小图中，只有4个达到了0.05以上的显著水平，4个达到了0.10的显著水平，而其他小图的红松针叶载量与林火蔓延速率没有表现出线性关系。图3和图4的比较研究表明，对于红松针叶床层而言，从统计上讲，载量对林火蔓延速率没有显著的影响。但在一定的可燃物床层条件下(如图4(d)、(l)、(t)蔓延速率与载量线性关系显著)，林火蔓延速率随载量增大而增加。这表明可燃物载量对林火蔓延速率的影响比较复杂:一种可能是两者之间的关系依赖于其他条件，如含水率或床层高度或压缩比等;另一种可能是两者之间没有关系，其中一些显著的相关是由于试验误差导致。

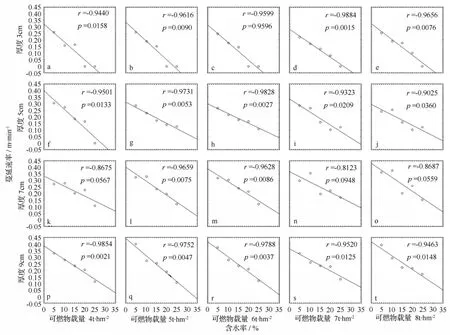
图2 可燃物床层载量和高度相同条件下的林火蔓延速率与可燃物含水率之间的关系

图3 林火蔓延速率与可燃物床层载量之间的关系(全部100次点烧试验数据)

2.2.3 红松针叶床层高度的影响

从图5中可见，红松针叶床层高度对林火蔓延速率具有较强的影响，随可燃物床层高度的增加，红松针叶床层的林火蔓延速率增加，显著水平超过0.0001。图6给出了相同可燃物载量和含水率时床层高度与红松针叶床层林火蔓延速率之间的关系。其中，各小图所表现出的可燃物床层高度与林火蔓延速率之间的关系也比较复杂:在25个小图中，6个达到了0.05以上的显著水平;5个达到了0.10的显著水平;其他小图中的可燃物高度虽与林火蔓延速率没有表现出简单的相关关系，但从相关系数上看，其关系要远比载量与林火蔓延速率之间的关系(图4)密切。因此，尽管从一定的可燃物床层条件下红松针叶床层林火蔓延速率与高度关系不紧密，但从统计或大量试验数据上看，高度对林火蔓延速率具有显著的影响。从图6中还可以看出，当可燃物含水率为5%和15%时，床层高度对林火蔓延速率的影响显著，含水率为10%时则不显著，而含水率为20%～25%则基本没有影响。这表明，床层高度对林火蔓延速率的作用可能与含水率有关，含水率越高，床层高度的影响越不明显，或者影响模式从线性向非线性过渡。

图4 可燃物含水率和床层高度相同条件下的林火蔓延速率与可燃物载量之间的关系(图4(e)为不持续燃烧数据)

图5 林火蔓延速率与可燃物床层高度之间的关系(全部100次点烧试验数据)

2.2.4 红松针叶床层压缩比的影响

图7给出了红松针叶床层压缩比和林火蔓延速率的关系。从图7中可见，压缩比对林火蔓延速率具有显著影响。在可燃物含水率不变的条件下，当载量和高度两个变量中的一个保持不变而另一个变化时(即2.2.2 和 2.2.3 中的试验)，可燃物床层压缩比也在变化。因此，图4和图6也可以用来研究剥离红松针叶床层压缩比对林火蔓延速率的影响，只是其变化与可燃物床层载量或高度同步。红松针叶床层压缩比与林火蔓延速率之间的相关系数与高度和林火蔓延速率之间的相关系数在绝对值上接近，因此，对于红松针叶床层而言，压缩比和高度对林火蔓延速率的影响是相似的，高度对林火蔓延的影响应通过改变可燃物床层的压缩比而发生作用。

2.3 红松针叶床层林火蔓延速率的预测模型

根据前面的分析，在加式模型(线性模型)中选择两个模型。第一个模型为林火蔓延速率R=b0+b1M+b2D(m·min－1)，其自变量为红松针叶含水率M、红松针叶床层高度D。由于2.2.1中的研究已表明红松针叶含水率对林火蔓延速率的影响与床层的其他特征无关，所以，含水率和床层高度的交互作用没有包括在模型中。另一个线性模型的自变量为红松针叶含水率M、可燃物床层压缩比B。与上同理，含水率与压缩比的交互作用也没有使用，故模型形式也是R=b0+b1M+b2D。实际上，在包括交互作用的上述模型中，交互作用的回归系数不显著，也需要从模型中剔除，这也进一步证实了2.2.1中关于红松针叶含水率对林火蔓延速率的影响独立于床层特征的分析。乘式模型也选择两个:第一个模型的自变量为可燃物含水率和床层高度，形为R=(b0+b1M)(b2+b3D):另一个模型的自变量为可燃物含水率和床层压缩比，形为R=(b0+b1M)(b2+b3B)。

图6 可燃物含水率和床层载量相同条件下的林火蔓延速率与可燃物床层高度之间的关系

图7 林火蔓延速率与可燃物床层压缩比之间的关系(全部100次点烧试验数据)

表2给出了4个模型的估计参数、误差和统计检验。其中，参数和统计检验为用100次点烧试验数据估计的结果，而误差为100次交叉验证的结果。从表2中的决定系数和平均绝对误差上看，同样形式的模型，以可燃物含水率和床层高度为预测因子的模型要比以含水率和床层压缩比为自变量的模型要好。采用同样预测因子时，加式模型比乘式模型好。其中，效果最好的模型是以可燃物含水率和床层高度为预测因子的加式模型，尽管其平均相对误差比相应的乘式模型略大一些。图8给出了该模型的预测值和实测值的对比，从中可见，该模型对红松针叶床层林火蔓延速率的预测在高估和低估方向上的比例基本是一致的，因此，模型是无偏的。但预测偏低的幅度要比预测偏高的幅度大。

图8 以含水率和床层高度为自变量的林火蔓延速率线性预测模型的预测值和实测值对比

表2 4个林火蔓延速率模型的参数和误差

3 结论与讨论

系统设计的室内点烧试验结果表明，平地无风条件下红松针叶床层的林火蔓延速率不超过0.4 m·min－1。红松针叶含水率、床层高度和压缩比对林火蔓延速率具有显著的影响。其中，含水率对林火蔓延速率的影响与可燃物床层的高度、载量等无显著关系，而可燃物床层高度和压缩比对林火蔓延的影响可能受可燃物床层特征的影响，需进一步研究确定。床层载量对红松针叶床层的林火蔓延速率影响不大。以可燃物含水率和床层高度为预测因子的线性林火蔓延速率预测模型能够解释85%的林火蔓延速率变差，模型的平均绝对误差为0.03 m·min－1，平均相对误差不超过13%。

研究中，有些点烧试验在20%的含水率时不燃，有些在25%的含水率时不燃。这与 Rothermel［11］研究中采用的固定熄灭含水率不同。灭绝含水率本身就是一个比较模糊的概念，并且许多环境因素和可燃物本身的属性都可能影响灭绝含水率的取值［25］(本文中可能与可燃物床层的结构有关)。Wilson［26］的研究表明，可燃物含水率对林火蔓延的持续性影响与可燃物床层结构有关。本文的研究与其相似，但由于不燃点烧试验的次数只有9次，还无法具体分析其中的联系，需进一步研究，以便更好地理解可燃物含水率对火行为的影响。

可燃物床层的载量、高度和压缩比对林火蔓延速率的影响比较复杂，Anderson［27］的研究表明，林火蔓延速率与可燃物载量正相关;Catchpole［28－29］认为，林火蔓延速率与可燃物床层高度关系不大;而Wilson［26］则认为，无风时林火蔓延速度正比于床层高度的平方根。本文的研究与Wilson［26］的结论相似，与其他研究相反。一些野外点烧试验，如Anderson［27］，受点烧时条件限制，一些可燃物床层特征变量的变化幅度可能较小，所得结果无法体现该变量对林火蔓延速率的影响。Catchpole［28－29］的研究与本研究试验条件相似，但所得结论与本研究相反，需进一步研究。

［1］郑焕能.森林防火［M］.哈尔滨:东北林业大学出版社，1992:24.

［2］舒立福，田晓瑞，马林涛.林业科学研究［J］.林火生态的研究与应用，1999，12(4):422－427.

［3］柴瑞海，赵雨森，杜秀文.大兴安岭林区草甸火顺风蔓延模型的研究［J］.东北林业大学学报，1998，16(4):90－93.

［4］王海晖，朱霁平.森林地表火行为估算的数学模型［J］.火灾科学，1994，3(1):33－41.

［5］袁春明，文定元.林火行为研究概况［J］.世界林业研究，2000，12(6):27－31.

［6］钟占荣，周建军，邹样辉，等.山地林火蔓延模型的研究［J］.火灾科学，2001，10(2):83－87.

［7］唐晓燕，孟宪宇，易浩若.林火蔓延模型及蔓延模拟的研究进展［J］.北京林业大学学报，2002，24(1):87－91.

［8］田晓瑞，王明玉，殷丽，等.大兴安岭南部春季火行为特征及可燃物消耗［J］.林业科学，2009，45(3):90－95.

［9］王明玉，李涛，任云卯，等.森林火行为与特殊火行为研究进展［J］.世界林业研究，2009，22(2):45－49.

［10］Sullivan A L.Wildland surface fire spread modeling，1990－2007.2:Empirical and quasi-empirical models［J］.International Journal of Wildland Fire，2009，18(4):369－386.

［11］Rothermel R C.A mathematical model for predicting fire spread in wildland fuels［R］.USDA:Forest Service Research Paper，1972:115.

［12］Stocks B J，Lynham T J，Lawson B D，et al.The Canadian system of forest fire danger rating system:An overview［J］.The Forestry Chronicle，1989，65(6):450－457.

［13］Forestry Canada Fire Danger Group.Development and structure of the Canadian forest fire behavior prediction system［R］.Ottawa:Forestry Canada，Science and Sustainable Development Directorate Information Report，1992.

［14］Taylor S W，Alexander M E.Science，technology，and human factors in fire danger rating:the Canadian experience［J］.International Journal of Wildland Fire，2006，15(1):121－135.

［15］Cheney N P，Gould J S，Catchpole W R.Prediction of fire spread in grasslands［J］.International Journal of Wildland Fire，1998，8(1):1－13.

［16］Gould J S，McCaw W L，Cheney N P，et al.Project vesta:Fire in dry eucalypt forest:Fuel structure，fuel dynamics and fire behaviour［M］.［s.l.］:Csiro Publishing，2007.

［17］Viegas D X，Almeida M，Miranda A I，et al.Linear model for spread rate and mass loss rate for mixed-size fuel beds［J］.International Journal of Wildland Fire，2010，19(5):531－540.

［18］崔文彬，乔启宇，牛树奎，等.地表火燃烧参数及其火头前影响区的实验研究［J］.北京林业大学学报，1998，20(5):22－27.

［19］Wotton B M，McAlpine R S，Hobbs M W.The effects of fire front width on surface fire behaviour［J］.International Journal of Wildland Fire，1999，9(4):247－253.

［20］Balbi J H，Santoni P A，Dupuy J L.Dynamic modeling of fire spread across a fuel bed［J］.International Journal of Wildland Fire，1999，9(4):275－284.

［21］Viegas D X，Matos P L P，Palheiro P.Slope and wind effects on fire spread［M］.Rotterdam:Forest Fire Research＆ Wildland Fire Safety，2002.

［22］Burrows N，Ward B，Robinson A.Fire behaviour in spinifex fuels on the Gibson Desert Nature Reserve，Western Australia［J］.Journal of Arid Environments，1991，20(2):189－204.

［23］Baeza M，De Luís M，Raventós J，et al.Factors influencing fire behaviour in shrublands of different stand ages and the implications for using prescribed burning to reduce wildfire risk［J］.Journal of Environmental Management，2002，65(2):199－208.

［24］McCaw L.Predicting fire spread in Western Australian mallee-heath shrubland［D］.Canberra:University of New SouthWales，1997.

［25］Jolly W M.Sensitivity of a surface fire spread model and associated fire behaviour fuel models to changes in live fuel moisture［J］.International Journal of Wildland Fire，2007，16(4):503－509.

［26］Wilson R A，Jr.Reexamination of Rothermel’s fire spread equations in no-wind and no-slope conditions［R］.USDA:Forest Service Research Paper，1990:434.

［27］Anderson H E，Brackebusch R P，Mutch RW，et al.Mechanisms of fire spread research progress report no.2［R］.USDA:Forest Service Research Paper，1966:28.

［28］Catchpole W R，Catchpole E A，Butler B W，et al.Rate of spread of free-burning fires in woody fuels in a wind tunnel［J］.Combustion Science and Technology，1998，131(1/6):1－37.

［29］Catchpole E A，Catchpole W R，Rothermel R C.Fire behavior experiments in mixed fuel complexes［J］.International Journal of Wildland Fire，1993，3(1):45－57.