基于开关算法的欠驱动刚体航天器姿态控制
2012-09-18朱家兴孙兆伟陈长春
朱家兴,孙兆伟,陈长春
(哈尔滨工业大学 卫星技术研究所,黑龙江 哈尔滨 150001)
0 引言
可靠性、安全性和有效性是航天产品品质的主要指标。对卫星等航天器来说,一旦发射入轨便成为不可维修系统,因此研究控制算法,保证航天器在部分执行机构发生故障时能全部或部分完成飞行任务,是挽救损失和提高系统可靠性的有效途径[1]。理论上,欠驱动系统属于二阶非完整系统,即系统加速度具有不可积性。文献[2]建立了二阶非完整系统的动力学与控制的理论框架,并分析了系统的可控性和可镇定性,为欠驱动控制领域的深入研究提供了基础。欠驱动系统是指由控制输入向量构成空间的维数小于位形空间维数的系统,即指控制输入数小于系统自由度的系统[3]。欠驱动航天器,是指姿态控制系统中的执行机构是非完整配置的航天器,即执行机构不能提供三轴独立的控制力矩[4]。由于研制、发射等费用巨大和几乎不可维修的特点,当部分执行机构发生故障时,设计者希望航天器控制系统仍具有令人满意的性能。欠驱动控制可为此提供一种备份技术,欠驱动航天器姿态控制的研究对提高整个控制系统的可靠性、延长航天器的使用寿命,具有重要的意义。
目前,欠驱动航天器的姿态控制已成为研究热点。文献[5]的研究表明,采用角动量交换装置作为执行机构的航天器,在系统总角动量不为零条件下,当控制输入的个数小于3时,系统将不可控;文献[6]认为仅有两个控制输入的刚体航天器,因不满足文献[7]的Brockett必要条件,不能由光滑状态反馈实现欠驱动控制。文献[8]针对欠驱动轴是否为对称轴,通过开关控制,分别提出非连续的反馈控制策略。文献[9、10]基于(w,z)参数,在欠驱动轴为对称轴和欠驱动轴初始角速度为零的假设条件下,设计了非连续反馈控制律,实现了欠驱动航天器姿态的渐近稳定。
本文利用开关算法,通过在不同控制律间的切换,研究了航天器姿态角速度和姿态角的欠驱动控制律设计。
1 刚体航天器姿态运动模型
1.1 姿态动力学方程
根据Euler方程,刚体航天器姿态动力学方程可表示为

式中:Ii(i=1,2,3)为航天器的主转动惯量;ωi为航天器相对惯性空间的角速度矢量在星体固联坐标系中的分量;Mi为外力矩矢量在星体固联坐标系中的分量。假设M3=0,即第三轴为欠驱动轴,则成立

式中:uj(j=1,2)为控制量,且uj=Mj/Ij;α1,α2,α3为与航天器主转动惯量有关的常数,且α1=(I2-I3)/I1,α2=(I3-I1)/I2,α3=(I1-I2)/I3。
1.2 姿态运动学方程
根据欧拉有限转动定理,将参考坐标系转动3次即可得星体固联坐标系,3次转过的欧拉角分别为滚动角φ,俯仰角θ,偏航角ψ,如图1所示。

图1 3-2-1顺序欧拉角Fig.1 Eulerian angles sequence 3-2-1
欧拉角(3-2-1顺序)参数描述的姿态运动学方程为:

2 欠驱动航天器姿态稳定控制
针对欠驱动轴是否为惯性对称轴,利用开关算法和退步控制技术,本文设计了实现欠驱动航天器姿态渐近稳定的控制律。刚体航天器的欠驱动控制较难处理的是对失控轴角速度的控制,因此本文先对姿态角速度进行稳定控制,再对姿态角进行稳定控制。
退步控制是一种基于李雅普诺夫稳定理论的控制器递推设计方法,一般用于控制量与被控量间存在一个或多个积分器的非线性系统[11]。退步控制设计过程如下:将一子系统(假设该子系统中不含直接控制量)中的其他状态变量视作“虚拟控制量”,按李雅普诺夫设计方法设计“中间控制律”,使该子系统的状态实现渐近稳定;引入误差变量,利用直接控制量设计误差系统,使真实状态变量与“虚拟控制量”间具有某种渐近特性,从而得到最终的退步控制律,实现整个系统的渐近镇定或跟踪。
设计欠驱动控制律需要用两个函数。对双积分系统

用退步控制算法,函数
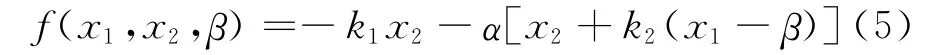
具有性质:在控制律u=f(x1,x2,β)作用下,可使双积分系统式(4)由任意初始状态到达最终状态(β,0)。此处:x1,x2分别为姿态角和姿态角速度;k1,k2,α均为大于0的控制参数;β为任意常数。不失一般性,令β=0,利用李雅普诺夫定理分析系统,可得
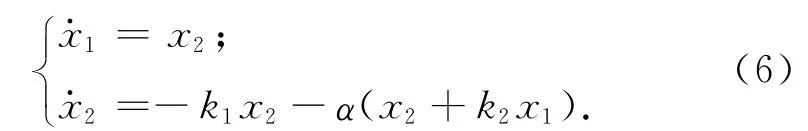
在原点处的平衡状态的稳定性。取李雅普诺夫函数

则有
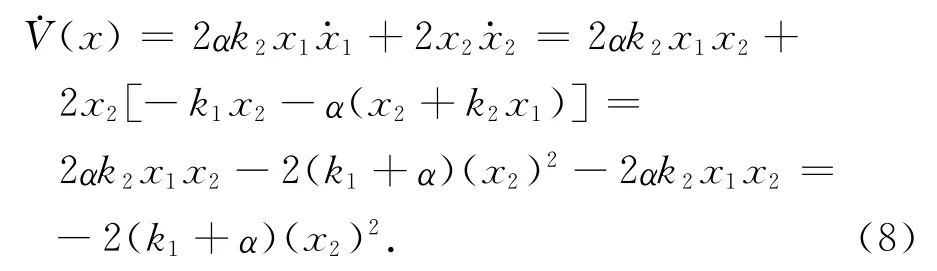
因V(x)正定,-V(x)半负定,故系统在原点处的平衡状态是稳定的。进一步分析可知,-V(x)=0所包含的最大不变集中仅有1个点(x1,x2)=(0,0),由LaSalle不变集定理可知,系统的状态最终会收敛至原点,即系统在原点处的平衡状态是渐近稳定的。

设[ω10ω20ω30φ0θ0ψ0]为描述航天器全局运动的初始状态,取控制目标为

2.1 姿态角速度稳定控制律设计
当欠驱动轴为非对称轴,即I1≠I2时,可通过姿态动力学之间的耦合进行三轴姿态角速度的控制。通过3次姿态机动,即可实现姿态角速度的稳定控制。
考虑欠驱动轴为非对称轴的航天器姿态动力学方程可表示为
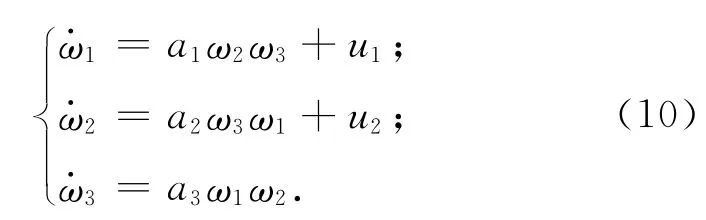
机动1:执行反馈控制律

式中:k3为大于0的控制参数;上标表示控制律的切换次数。在此控制律作用下,ω1,ω2,很快衰减为零,且当ω1=ω2=0时,将有ω3=(常数)。此处:ω3为绕欠驱动轴旋转的自旋角速度。
机动2:执行反馈控制律

机动3:执行反馈控制律

在此控制律作用下,经过有限时间t=/k3,将再次有ω1=ω2=0,积分可得,此时ω3=0,即系统的姿态角速度收敛至状态[ω1ω2ω3]=[0 0 0]。
至此,实现了欠驱动刚体航天器姿态角速度的稳定控制。
2.2 姿态角稳定控制律设计
在姿态角速度收敛的基础上,利用函数f(x1,x2,β),根据姿态运动学方程,每次只利用1个控制力矩,通过改变姿态角速度ω1,ω2,进而改变一个姿态角,5次机动后,即可实现姿态角稳定控制。
考虑姿态运动学方程

机动4:执行反馈控制律

直至φ=0,ω=0,即系统的状态转移至

该次机动仅用到控制力矩u1。前4次机动后,有。
机动5:执行反馈控制律

直至θ=0,ω2=0,即系统的状态转移至

该次机动仅用控制力矩u2。在前5次机动的基础上,再次有。
机动6:执行反馈控制律

直至φ=0.5π,ω1=0,即系统的状态转移至

该次机动仅用到控制力矩u21。在前6次机动的基础上,将有。
机动7:执行反馈控制律

直至ψ=0,ω2=0,即系统的状态转移至
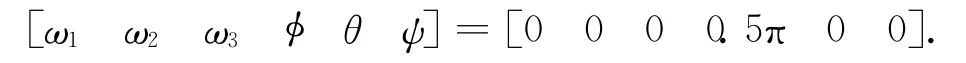
该次机动仅用到控制力矩u2。在7次机动的基础上,又有。
机动8:执行反馈控制律

直至φ=0,ω1=0,即系统的状态转移到了目标状态

根据精度要求决定是否重新执行机动1。由此实现了欠驱动航天器姿态渐近稳定控制。
2.3 欠驱动轴为对称轴的航天器姿态稳定
当欠驱动轴为对称轴,即I1=I2时,姿态动力学方程式(2)变为
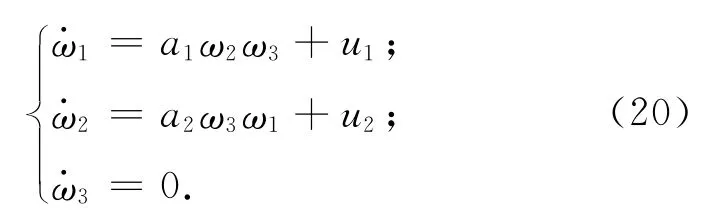
可知ω3恒为常值,且不可控。此时若假设ω3(0)=0,可得简化模型。文献[6]证明简化模型在任意平衡点是“短时间局部可控的”,从而可进行非连续控制律设计。
此时,只需经过6次机动即可实现轴对称欠驱动刚体航天器的姿态控制,其分析过程同欠驱动轴为非对称轴情况类似。
3 仿真
3.1 非轴对称欠驱动航天器姿态控制
采用控制律式(11)~(13)、(15)~(19)对系统式(10)、(14)进行稳定。取控制参数k1=k2=0.25,α=0.8,k3=0.7;转动惯量常数α1=α2=-1,α3=-0.42857;姿态角速度的初值为ω(0)=[0.05-0.04-0.03]rad/s,姿态角初值为φ0=π/3,θ0=π/6,ψ0=π/4,仿真结果如图2~4所示。
由仿真结果可知:在t=20s左右时,姿态角速度收敛至零附近;在t=50s左右时,控制律式(15)作用,滚动角φ收敛至零;在t=75s左右时,控制律式(16)作用,俯仰角θ收敛至零;在t=125s左右时,控制律式(17)作用,滚动角φ收敛至π/2;在t=155s左右时,控制律式(18)作用,偏航角ψ收敛至零;在t=225s左右时,控制律式(19)作用,滚动角φ再次收敛至零;在t=350s左右时,姿态角速度和姿态角均收敛至零附近,姿态角的控制精度达到5×10-2(°),验证了本文控制律的有效性。

图2 姿态角速度Fig.2 Attitude angular velocity
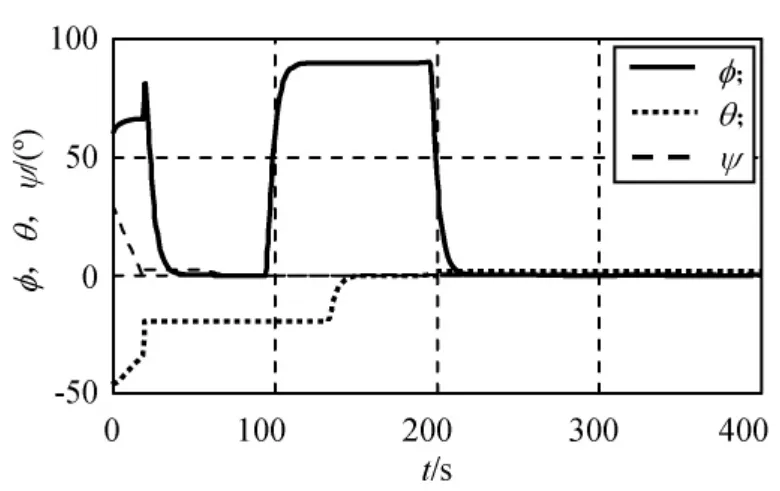
图3 姿态角Fig.3 Attitude angle

图4 控制输入Fig.4 Control input
3.2 轴对称欠驱动航天器姿态控制
采用控制律式(11)、(15)~(19)对系统式(20)、(14)进行稳定。取控制参数k1=k2=0.2,α=0.5,k3=0.5;惯量常数α1=-0.2,α2=0.2;姿态角速度初值ω(0)=[0.001 2-0.001 25]rad/s,姿态角初值φ0=π/2,θ0=π/4,ψ0=π/2,仿真结果 如 图5~7。

图5 姿态角速度Fig.5 Attitude angular velocity

图6 姿态角Fig.6 Attitude angle
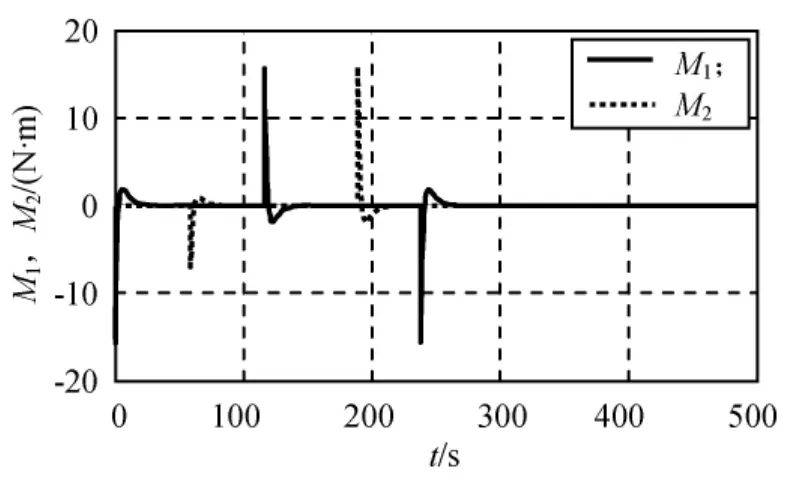
图7 控制输入Fig.7 Control input
由仿真结果可知:在t=40s左右时,控制律式(15)作用,滚动角φ收敛至零;在t=100s左右时,控制律式(16)作用,俯仰角θ收敛至零;在t=150s左右时,控制律式(17)作用,滚动角φ收敛至π/2;在t=230s左右时,控制律式(18)作用,偏航角ψ收敛至零;在t=200s左右时,控制律式(19)作用,滚动角φ再次收敛至零;在t=500s左右时,姿态角速度和姿态角均收敛至零附近,姿态角的控制精度达到5×10-3(°),验证了本文控制律的有效性。
4 结束语
本文对执行机构只能提供两轴独立控制力矩的欠驱动航天器的姿态控制进行了研究。利用开关算法和退步控制技术,通过在不同控制律间的切换,分别设计了姿态角速度稳定和姿态角稳定的控制律,实现了欠驱动刚体航天器姿态渐近稳定控制律的设计。数值仿真结果验证了该控制律的有效性,以及良好的动态过程和控制精度。本文控制律的优点是可在有限时间内实现航天器姿态渐近稳定,缺点主要是因采用不同控制律间的切换实现稳定控制,鲁棒性较差,对存在干扰和惯量积非零情况也需进一步研究。
[1]徐福祥.卫星工程概论[M].北京:宇航出版社,2003:352.
[2]REYHANOGLU M,Van Der SCHAFT A J,McCLAMROCHN H,etal.Nonlinear control of a class of underactuated systems[C]//IEEE Conference on Decision and Control.Kobe:IEEE,1996:1682-1687.
[3]周祥龙,赵景波.欠驱动非线性控制方法综述[J].工业仪表与自动化装置,2004(5):10-13.
[4]王 芳,张洪华.欠驱动刚性航天器旋转轴稳定研究[J].宇航学报,2007,28(5):1133-1137.
[5]CROUCH,P E.Spacecraft attitude control and stabilization:application of geometric control theory to rigid body models[J].IEEE Transactions on Automatic Control,1984,29(4):321-331.
[6]BYRNES C I,ISIDORI A.On the attitude stabilization of a rigid spacecraft[J].Automatica,1991,27(1):87-95.
[7]BROCKETT R W.Asymptotic stability and feedback stabilization[J].Differential Geometric Control Theory,1983,6(1):181-191.
[8]KRISHNAN H,REYHANOGLU M,McCLAMROCH H.Attitude stabilization of a rigid spacecraft using gas jet actuators operating in a failure mode[C]//Proceedings of the 31th Conference on Decision and Control.[s.l.],IEEE:1992:1612-1617.
[9]TSIOTRAS P,LONGUSKI M.A new parameterization of the attitude kinematics[J].Journal of the Astronautical Sciences,1995,43(3):243-262.
[10]TSIOTRAS P,CORLESS M,LONGUSKI M.A novel approach to the attitude control of axi-symmetric spacecraft[J].Automatica,1995,31(8):1099-1112.
[11]郑敏捷,徐世杰.欠驱动航天器姿态控制系统的退步控制设计方法[J].宇航学报,2006,27(5):947-951.
