自选子密钥的动态门限多重秘密共享方案*
2012-09-17白雪鹏刘焕平
白雪鹏,刘焕平
(哈尔滨师范大学)
0 引言
秘密共享是信息安全和数据保密中的重要手段.秘密共享的概念在1979年由Shamir[1]和Blakle[2]分别独立的提出,其思想是将要共享的秘密以适当的方式拆分成n个不同份额,分别由不同的参与者管理,每个参与者不知道其他人的份额,只有至少m个参与者联合才可以重构该秘密,而少于m个参与者合作不能得到共享的秘密.其缺点是当一个秘密重构后,各参与者的秘密份额将失效,要想共享新的秘密必须重新分配子密钥.所以秘密共享的关键是如何更好的设计秘密拆分方式和重构方式,使每个参与者子密钥多次使用,提高效率.
2009年,Parakh和Kak提出了一个秘密共享方案[3],该方案是把一个秘密分成k-1个部分,采用递归方法,重构秘密时按sk-1,…,s1的顺序,用“后入先出”的方式进行,但其有四处不足.在其基础上该文提出了一个自选子密钥可验证的动态门限多重秘密共享方案.其他部分组织如下:第1节简述Parakh等人的方案并加以分析,指出其不足之处;第2节介绍我们的方案;第3节对新的方案进行性能分析;第4节得出结论.
1 Parakh等人的方案
对于一个秘密S,我们利用(k,n)门限方案来共享.出于对信息分散管理的目的,首先把秘密S分成k-1个部分(有关秘密的划分在文献[4]中做了详细阐述),这些部分记为si,1≤i≤(k-1),使得它们的级联s1s2…sk-1=S.以下运算都是在Zp中进行.
1.1 秘密分发
(1)选择一个素数p,p>max(smax,n),这里smax=max(si),1 ≤i≤(k-1),s1,s2,…,sk-1是秘密S的k-1个部分.
(2)在Zp中均匀随机选取一个数a1,构造一个多项式p1(x)=a1x+s1.
(3)计算p1(x)在1,2处的函数值,记为p1(1)=Ds11,p1(2)=DS12,表示s1的两个份额.
(4)当2≤i≤(k-1)时
(a)生成多项式,
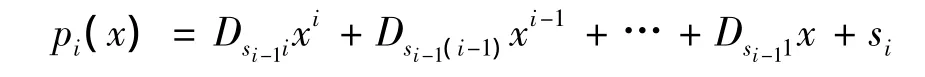
(b)计算pi(x)在不同x处的函数值,令它们成为新份额,
(i)如果i<k-1,计算i+1个点的值:
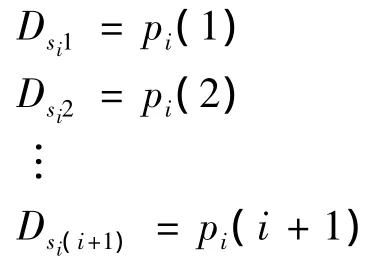
(ii)如果i=k-1,计算n个点的值:

(c)删除旧份额:Dsi-11,Dsi-12,…,Dsi-1i.
(5)最后得到的n个值作为n个参与者的份额,每个参与者得到点对(i,Di),1≤i≤n.
1.2 秘密恢复
(1)利用k对(i,Di)和Lagrange插值法构造k-1次多项式

并且计算sk-1=pk-1(0).
(2)计算i=k-2直到1
(a)从pi+1(x)的系数中得到i+1个点对(m+1,Dsi(m+1)),0≤m≤i,利用Lagrange插值法构造i次多项式.

(b)计算si=pi(0).
1.3 方案分析
上述方案存在四处不足:
(1)秘密分发者为各参与者分配子密钥,这需要安全信道;
(2)秘密S被分拆成k-1个部分s1,s2,…,sk-1,其分拆的数目受到了门限值k的制约,使方案的灵活性受到限制,这种情况不是我们所希望的;
(3)在秘密分发过程中,Dsk-2k-1可能为0,此时生成多项式pk-1(x)的次数小于k-1次,所以这时少于k个人也能恢复出此秘密.即使在分发过程中,最后系统发现pk-1(x)不是k-1次多项式而重新选取a1,这个过程也是十分耗时的;
(4)每次只能恢复一个秘密;当要共享新的秘密时,参与者的子密钥需要重新分配.对于以上不足之处,我们加以改进并在其基础上提出一个动态秘密共享方案,使用(m,n)门限方案共享k个秘密,其中k是不大于n的任意正整数,秘密按sk,sk-1,…,s1的顺序恢复.并且该方案可自选子密钥、可验证参与者是否有欺骗行为,当要共享新一轮秘密时不需要重新分配子密钥.
动态秘密共享方案[5-7]是指参与者集合有成员加入或离开这种动态变化时,其他成员所持子密钥可反复使用的共享体制.
2 我们的方案
定义1 (双变量单向函数[8])双变量单向函数f(r,s)表示一个有两个变量的单向函数,能够将任意长的变量r和s映射为固定长的函数f(r,s).双变量单向函数具有以下六个性质:(1)已知r和s,容易计算出f(r,s);(2)已知s和f(r,s)求r,在计算上是不可行的;(3)未知s的情况下,对于任意r难以计算f(r,s);(4)给出s,找到不相等的r1和r2满足f(r1,s)=f(r2,s)是不可行的;(5)已知r和f(r,s)求s,在计算上是不可行的;(6)已知任意多的(ri,f(ri,s))对,求f(r',s)是不可行的,其中r'≠ri.
2.1 系统初始化
(1)系统DC选两个大素数p和q,N=p×q,再随机选取整数e∈[2,N],且与(p-1)和(q-1)互素.找到d,满足e×d=1 modφ(n),φ(n)表示euler函数.公开e,保密d.
(2)设f(r,s)是从GF(p)×GF(p)到GF(p)上的一个双变量单向函数.系统DC随机选t∈GF(p)并公开.每个参与者pi(i=1,…,n)随机选子密钥ui∈GF(p),令f(ui,t)=,计算,并公开发送给DC.系统DC计算modN=i,i=1,2,…,n,确保i≠
(3)系统 DC 计算vi=f(f(ui,t),t)=f(,t),i=1,2,…,n,并公开vi.
2.2 秘密分发
系统DC确保an≠0,否则要求部分参与者重新选取子密钥.公开pk(n+1),pk(n+2),…,pk(2n-m+1).
(2)计算j=k-1直到1,令Dsj1=pj(1),…,Dsjj=pj(j)利用pj(1),pj(2),…,pj(j)和(0,sj)这j+1个点构造j次多项式,记为:
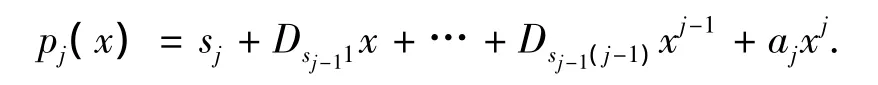
公开pj(j+1).
2.3 秘密恢复
(1)秘密按sk,sk-1,…,s1的顺序恢复,至少m个成员,不妨设p1,p2,…,pm提供1,2,…,.参与者们计算f(,t),j=1,2,…m,并判断与公告牌上的vj是否相等.若相等则没有欺骗行为,继续执行下一步;否则终止秘密恢复.
(2)参与者提交的m个点(i,),i=1,2,…,m,公开的n-m+1 个点,pk(n+1),pk(n+2),…,pk(2n-m+1)共n+1个点,利用Lagrange插值法构造n次多项式

从而得到sk=pk(0).
(3)计算j=k-1直到1.
从pj+1(x)的系数中得到Dsj1=pj(1),…,Dsjj=pj(j),即j个点对,1 ≤j≤j,从公告牌上下载pj(j+1),利用这j+1个点和Lagrange插值法构造j次多项式

计算sj=pj(0).
3 性能分析
3.1 参与者动态改变
当增加或删除参与者时,都只须分发者D进行修改,而其他参与者不须做改变.
增加参与者pn+1时,(1)参与者随机选取子密钥un+1∈GF(p),计算,并公开发送给系统DC;(2)DC计算,确保1,2,…,n,否则令pi,pn+1更换各自子密钥重新计算,直到不相等为止;(3)DC根据新成员提供的子密钥重新计算,在秘密分发过程中对公开值做更改.
删除参与者pi时,系统DC在分发过程中经过计算、更改公开值即可.
3.2 安全性
该方案的安全性基于RSA体制中大整数分解问题的困难性和双变量单向函数的单向性.攻击者在已知和e的情况下,要想知道在计算上是不可行的.已知t和f(ui,t)求ui,在计算上是不可行的,即每个参与者的子密钥不会被系统DC及其他人知道.
3.3 确认欺骗者
系统DC为每个参者pi公开一个检测信息vi=f(f(ui,t),t),在秘密恢复时,任何人都可以通过等式vi=f(f(ui,t),t)是否成立来判断Pi是否是欺骗者.由于f(r,s)是单向函数,所以其他参与者不能通过DC公布的vi,t来获得pi的屏蔽子密钥f(ui,t)和子密钥ui.
3.4 子密钥复用
在秘密恢复过程中,参与者提供的是屏蔽子密钥,子密钥不会被其他人知道.当要共享新一轮秘密时,只需更改t值,使得屏蔽子密钥改变,而参与者子密钥可继续使用.
4 结束语
该文分析了Parakh和Kak所给出的秘密共享方案,并指出了方案中的缺陷,提出了一个新的自选子密钥可验证的动态门限多重秘密共享方案,不需要更改参与者的子密钥便可多次共享秘密,并且不需要安全信道.
[1] Shamir A.How to share a secret[J].Communications of ACM,1979,22(11):612-613.
[2] Blakley G R.Safeguarding cryptographic keys[C].AFIPS 1979 Natl Conf,New York,1979.313-317.
[3] Parakh A,Kak S.Space Efficient Secret Sharing:A Recursive Approach[R].arXiv:0901,4814v1[cs.CR]Jan Cryptology Print Archive,2009.365.
[4] Rabin M O.Efficient dispersal of information for security,load balancing and fault tolerance.Journal of the ACM,1989,36(2):335-348.
[5] 黄东平,王华勇,黄连生,等.动态门限秘密共享方案[J].清华大学学报:自然科学版,2006,46(1):102-105.
[6] 王天成,张建中.一个动态门限多重秘密共享方案[J].计算机工程与应用,2009,45(33):75-76.
[7] 林静丽,刘焕平.高效可验证动态门限秘密共享方案[J].密码与信息安全学报,2011,8(23):42-44.
[8] 庞辽军,柳毅,王育民.一个有效的(t,n)门限多重秘密共享体制[J].电子学报,2006,34(4):587-589.
