关于同时保持极小秩和某一非奇异双线性函数的变换*
2012-09-17金明浩
贺 丹,金明浩
(黑龙江工程学院)
0 引言
线性保持问题是矩阵论研究领域中一个十分活跃的课题,刻画矩阵集之间保不变量的线性算子的问题被称为“线性保持问题”,简称“LPP”(Linear preserve Problem).近年来,线性保持问题被广泛地研究,许多数学家通过加强、减弱、改变条件得到了很多成果[1-3].1991年Omladic M,Semel P考虑用“加法算子”代替线性算子[4-5],开始了“加法保持问题”的研究,可见加法保持问题是线性保持问题的推广.2005年Zheng B D,Sheng Y Q得到了结论:Mn(F)上的变换T是可逆线性变换当且仅当T部分地保持某一非奇异双线性函数[6].该文考虑Mn(F)到其自身的同时保持极小秩和某一非奇异双线性函数的变换T,给出了这种变换的详细刻画.
1 预备知识
设F是一个特征不为2的域,Mn(F)是F上n×n全矩阵空间,Ⅰ是n×n单位矩阵,GLn(F)是所有n×n可逆矩阵构成的群,称为一般线性群,F*是由F中所有非零元构成的乘法群.对于矩阵A∈Mn(F),记At是A的转置矩阵,A-1是A的逆矩阵,A*是A的伴随矩阵,Un(F)={A∈GLn(F)|AAt=Ⅰn}是酉群,r(A)是A的秩,mr(A)=min(r(A-λⅠ):λ∈F)是A的极小秩.若线性变换T:Mn(F)→Mn(F)满足mr(T(A))=mr(A),∀A∈Mn(F),则称T是Mn(F)上保持极小秩的线性变换.
对于矩阵A∈Mn(F),它的极小秩与其非平凡不变多项式的个数之间满足关系mr(A)+i(A)=n,其中i(A)表示A的非平凡不变多项式的个数[7].所以方阵平凡不变多项式的个数等于极小秩.因此研究保持平凡不变多项式的个数、非平凡不变多项式的个数、极小秩的变换是一回事.
如果对于某一非奇异双线性函数f(·,·):Mn(F)×Mn(F)→F来说,有Mn(F)上的变换T满 足f(A,B)=f(T(A),T(B))∀A,B∈Mn(F),则称T保持某一非奇异双线性函数
f(·,·):Mn(F)×Mn(F)→F.如果存在Mn(F)的一组基{ε1,ε2,…,εn}和一个映射π:{ε1,ε2,…,εn}→Mn(F),使 得f(A,εj)=f(T(A),π(εj))∀A∈Mn(F),j=1,2,…,n,则称T部分地保持某一非奇异双线性函数f(·,·):Mn(F)×Mn(F)→F.由文献[6]可知Mn(F)上的变换T是可逆线性变换当且仅当T部分地保持某一非奇异双线性函数.
2 主要结果
文献[8]刻画了Mn(F)到自身的保持极小秩的线性变换的形式.该文考虑Mn(F)到Mn(F)的同时保持极小秩和某一非奇异双线性函数的变换T,给出了这种变换的详细刻画.
定理1n≥3时,变换T:Mn(F)→Mn(F),如果满足

那么存在矩阵P∈GLn(F),使得
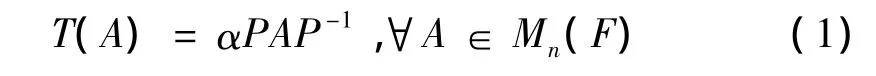
或者

其中α=±1.
反之,Mn(F)上任意形如(1),(2)的变换都满足条件(i)和(ii).
证明 由文献[6]可知T是线性的,再由文献[8]可得存在矩阵P∈GLn(F),使得

或者T(A)=αPAtP-1+f(A)Ⅰ,∀A∈Mn(F)
其中α∈F*,f是Mn(F)上的线性函数.
(1)当T(A)=αPAP-1+f(A)Ⅰ,∀A∈Mn(F)时,由条件(ii)可得对于任意A,B∈Mn(F),有

当B=Ⅰ时,Tr(A)=α2Tr(A)+αf(Ⅰ)Tr(A)+αf(A)n+nf(A)f(Ⅰ),∀A∈Mn(F),由此可得
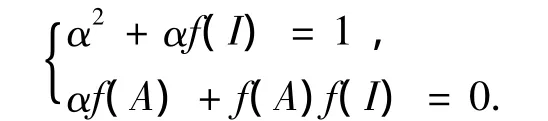
故f(A)=0,∀A∈Mn(F),因此f=0,α= ±1,即T(A)=αPAP-1,∀A∈Mn(F),其中α=±1.
(2)当T(A)=αPAtP-1+f(A)Ⅰ,∀A∈Mn(F)时,证明和(1)类似,略.
定理的第二部分是显然的,略.
对于域F来说,记F2={a2|a∈F}.
定理2n≥3时,变换T:Mn(F)→Mn(F),且F2=F,如果满足

那么存在矩阵P∈Un(F)={P∈GLn(F)|PtP=Ⅰn},使得
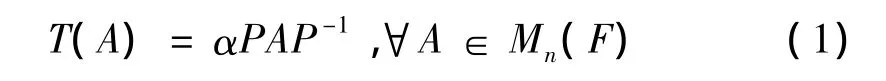
或者

其中α=±1.
反之,Mn(F)上任意形如(1),(2)的变换都满足条件(i)和(ii).
证明 由文献[6]可知T是线性的,再由文献[8]可得存在矩阵P∈GLn(F),使得

或者

其中α∈F*,f是Mn(F)上的线性函数.
(1)当T(A)=αPAP-1+f(A)Ⅰ,∀A∈Mn(F)时,由条件(ii)可得对于任意A,B∈Mn(F),有
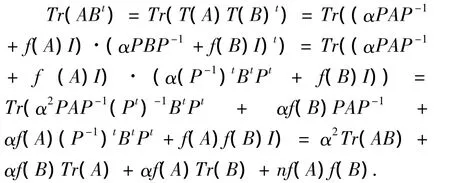
当B=Ⅰ时,Tr(A)=α2Tr(A)+αf(Ⅰ)Tr(A)+αf(A)n+nf(A)f(Ⅰ),∀A∈Mn(F),由此可得

故f(A)=0,∀A∈Mn(F),因此f=0,α=±1,即T(A)=αPAP-1,∀A∈Mn(F),其中α=±1.
因为对于任意A,B∈Mn(F),有

所以A=(PtP)A(PtP)-1,∀A∈Mn(F),即A(PtP)=(PtP)A,∀A∈Mn(F),则PtP是数量矩阵,设PtP=Ⅰn,因为F2=F,所以我们可以记=a2.对于可逆矩阵a-1P来说,(a-1P)t·a-1P=a-1Pt·a-1P=a-2(PtP)=a-2Ⅰ=a-2a2Ⅰ=Ⅰ,也就是存在矩阵P∈Un(F)={P∈GLn(F)|PtP=Ⅰ},使得T(A)=αPAP-1,∀A∈Mn(F),其中α=±1.
(2)当T(A)=αPAtP-1+f(A)Ⅰ,∀A∈Mn(F)时,证明和(1)类似,略.
定理的第二部分是显然的,略.
定理3n≥3时,变换T:Mn(F)→Mn(F),如果满足

那么存在矩阵P∈GLn(F),使得

或者

其中α=±1.
反之,Mn(F)上任意形如(1),(2)的变换都满足条件(i)和(ii).
证明 由文献[6]可知T是线性的,再由文献[8]可得存在矩阵P∈GLn(F),使得

或者

其中α∈F*,f是Mn(F)上的线性函数.
(1)当T(A)=αPAP-1+f(A)Ⅰ,∀A∈Mn(F)时,由条件(ii)可得对于任意A,B∈Mn(F),有


故f(A)=0,∀A∈Mn(F),因此f=0,α±1,即T(A)=αPAP-1,∀A∈Mn(F),其中α=±1.
(2)当T(A)=αPAtP-1+f(A)Ⅰ,∀A∈Mn(F)时,证明和(1)类似,略.
定理的第二部分是显然的,略.
定理4n≥3时,变换T:Mn(F)→Mn(F),如果满足

那么存在矩阵P∈GLn(F),使得
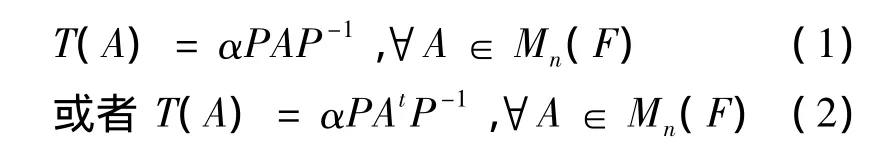
其中α=±1.
反之,Mn(F)上任意形如(1),(2)的变换都满足条件(i)和(ii).
证明 由文献[6]可知T是线性的,再由文献[8]可得存在矩阵P∈GLn(F),使得

或者

其中α∈F*,f是Mn(F)上的线性函数.
(1)当T(A)=αPAP-1+f(A)Ⅰ,∀A∈Mn(F)时,由条件(ii)可得对于任意A,B∈Mn(F),有

当B=Ⅰ时,B*=Ⅰ,因此

故f(A)=0,∀A∈Mn(F),因此f=0,α=±1,即T(A)=αPAP-1,∀A∈Mn(F),其中α=±1.
(2)当T(A)=αPAtP-1+f(A)Ⅰ,∀A∈Mn(F)时,证明和(1)类似,略.
定理的第二部分是显然的,略.
[1] Li C K ,Pierce S.Linear preserver problems[J].Amer.Math.Monthly,2001,108:591-605.
[2] Liu S W,Zhao D B.Introduction to Linear Preserver Problems[M].Harbin Press,Harbin,China,1997.1-23.
[3] Guterman A,Li C K,Semrl P.Some general technigues on linear preserve problems[J].Linear Algebra Appl,2000,315:61-81.
[4] Omladic M,Semrl P.Additive mappings preserving operators of rank one[J].Linear Algebra Appl,1993,182:239-256.
[5] 张显,曹重光.保不变量的矩阵加群同态[M].哈尔滨:哈尔滨出版社,2001.
[6] Zheng Baodong,Sheng Yuqiu.On transformation partly preserving a nonsingular bilinear function[J].Linear Algebra Appl,2005,403:273-284.
[7] Oliveira G N,Sa E M,Da Silva J AD.On the eigenvalues of the matrix[J].Linear and Multilinear Algebra,1977,5:119-128.
[8] 陈嘉佳,谭宜家.关于矩阵空间上保持极小秩的线性算子[J].福州大学学报,2007,35(1):6-8.
