基于Clifford代数的多光谱图像边缘检测

刘 辉 徐 晨 曹文明

(深圳大学信息工程学院，深圳 518000)

基于Clifford代数的多光谱图像边缘检测

刘 辉 徐 晨 曹文明

(深圳大学信息工程学院，深圳 518000)

为了充分利用多光谱图像不同图层之间的关联性，采用Clifford代数描述多光谱图像.在Clifford代数空间中，定义了多光谱图像的Clifford微分与Clifford梯度.在此基础上，提出了一种新的多光谱图像边缘检测与融合算法.该算法首先计算出各像素点的Clifford梯度，进而得到Clifford梯度范数;然后以此为依据，判断像素点是否为边界点，从而得到多幅边缘检测图像;最后，将这些图像融合，便可得到最终的边缘图像.与基于最大熵的多光谱图像边缘检测算法的比较结果表明，算法由于利用了多光谱图像不同图层之间的关联性，因而可以更好地保留边缘信息，获得更完整的边缘检测效果.

多光谱图像;边缘检测;Clifford代数;Clifford梯度;图像融合

多光谱图像是指利用多光谱传感器同时在多个窄的光谱波段上对同一对象(地域或目标)进行观测所获得的图像，反映了观测对象在各个窄光谱波段上的反射、透射或辐射特性.随着多光谱成像技术的飞速发展，多光谱图像被广泛应用于军事国防、医学图像分析、环境检测、地质勘探、航空/航天、反恐怖安全检测、农业产量评估、仿生识别、太空探索等领域［1-4］.

近年来，多光谱图像的边缘检测备受关注.其研究方法大多是将多光谱像素看作是N维向量空间中的点，利用向量空间数学和概率统计进行图像综合处理［5-9］.文献［8］提出了基于最大熵的多光谱图像边缘检测算法，其核心在于定义了多光谱图像的最大熵估算子，根据边缘谱值集中于高频区的特点，利用最大熵来提取边缘.文献［9］提出了一种基于非参数局部强度估算的多光谱图像边缘检测算法，通过非参数核估算子来估算图像强度，利用移动窗口得到局部强度的最小值.由于向量代数的局限性，这些传统算法在处理多光谱图像时不能很好地利用多光谱图像中不同图层间的关联性，而基于非传统向量代数的算法则可解决这一问题［10-12］.

本文提出了一种新的多光谱图像边缘检测与融合算法.试验结果表明，该算法利用了不同波段光谱层之间的关联性，在检测与融合中能较好地识别多光谱图像的模糊边缘，从而提高了检测精确度，更完整地保存了多光谱图像的边缘.

1 多光谱图像的Clifford代数描述

1.1 Clifford代数基础

设 e1，e2，…，ep+q－1，ep+q为向量空间V的一组正交基，其二项式是标准正交的，即Q(el)=±1或0，且当l≠m时Q(elem)=0.在反对称张量空间Λ(V)中可以定义如下的Clifford积［13］:

用符号Clp，q表示向量空间Vp+q上的 Clifford代数，其正交代数基为

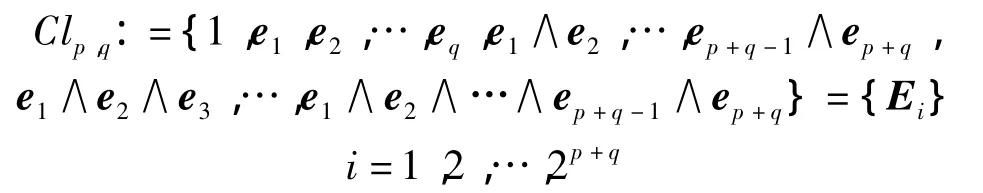
本文中，p=n，q=0.例如，Cl3的正交代数基为Cl3:={1，e1，e2，e3，e1∧e2，e1∧e3，e2∧e3，e1∧e2∧e3}.

在Cln上，任意多重矢量X可以表示为正交代数基的线性组合形式xiEi.X的k维向量部分的级数算子可以表示为〈X〉k，则

任意多重矢量X的逆为¯X，其计算公式为

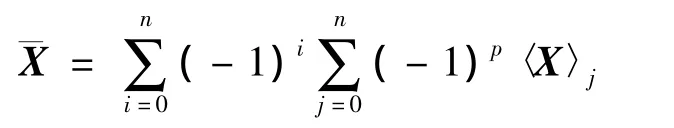
式中

1.2 多光谱图像描述

假设多光谱图像数据的波长采集范围为b～a，采集步长为c，则采集的多光谱图像的信息数据的三维矩阵，其中w和h分别为图像的宽和高取值为整数n，由此可将此矩阵记为Mn×w×h.将矩阵的波长维看作空间Clifford代数的向量维，则Mn×w×h的像素点可以用n维互相垂直的空间向量 el表示，并且满足 e2l=－1.Mn×w×h的像素点P用Clifford代数的n重矢量描述为

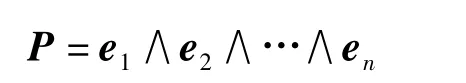
在Cln空间中，n重矢量是唯一的.如果将n维矢量空间中的一个点P采用二重矢量描述，则需要C2n个二重矢量，即

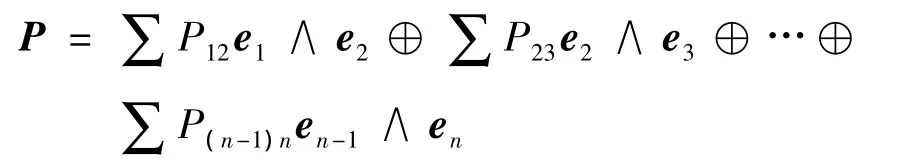
假设 2 幅多光谱图像分别为 Un1×w1×h1和Vn2×w2×h2，对应的 Clifford 代数空间正交基分别为{Er}和{Fs}，其中r=2n1，s=2n2.由此便可用函数来表示这2幅图像的一种融合，其中ur和vs分别表示各自图像数据矩阵对应波段处的元素值.

n维多光谱图像f(x')可以解释为多值信号，形如.其中，fi(x')为信号分量，x'∈Rn，i=0，1，…，n－1;1col，εcol，…，εn－1col为虚构单元，且 εncol=1.从Clifford代数的角度而言，f(x')被称为多重代数，可以表示为实数域和复数域的直和［14］，即

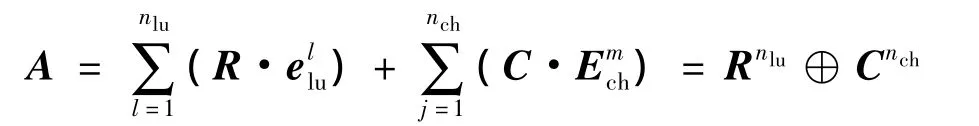
式中分别为实数域和复数域上直交幂等单元.本文中，nlu=1，2;n为偶数时nch=n/2，n为奇数时nch=(n－1)/2.

任意多重矢量e都能表示为标量部分和复数部分的线形组合，即

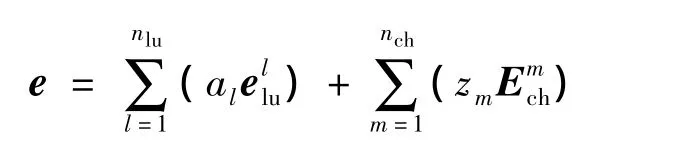
式中，ai∈R为多光谱强度数;zj为多光谱色度数.因此，n维多光谱图像可以描述为如下的Clifford代数形式:

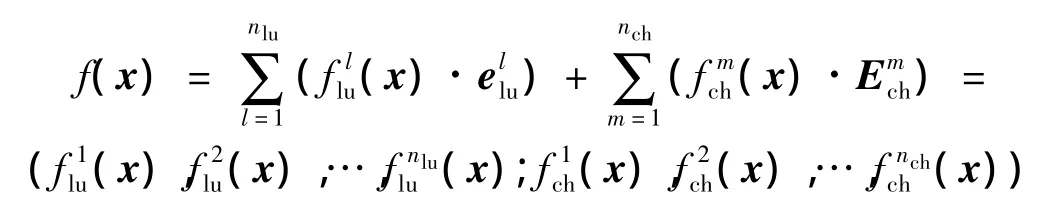
式中，x为Clifford代数的n维矢量.

2 多光谱图像边缘检测与融合

2.1 Clifford微分和Clifford梯度

定义1 多光谱图像多重矢量X的微分定义为

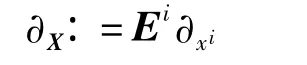
式中，Ei为 Ei的对偶基，即 Ej*Ei=δji.

定义2 设A∈Cln且A:=aiEi，则多光谱图

像的多重矢量函数f在A方向上的导数为

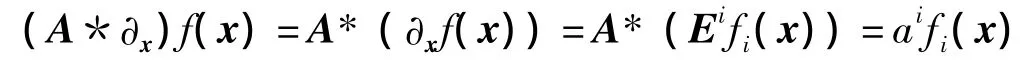
式中，A＊∂x为多光谱图像的多重矢量导数.

定义3 设f:Cln→R为f的标量函数，则Clifford空间下函数f的梯度定义为

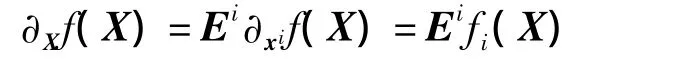
式中，fi(X):=∂xif(X)为f关于xi的偏导数.

当f:Cl1n→R为一重矢量的标量函数时，其梯度可以表示为∂xf(x)=ei∂xif(x)=eifi(x).

2.2 基于Clifford代数的边缘检测与融合算法

本文提出的基于Clifford代数的边缘检测与融合算法是通过求解多光谱图像的Clifford梯度来获取图像边缘的.

假设多光谱图像数据是一个三维矩阵，其像素点的光谱梯度为

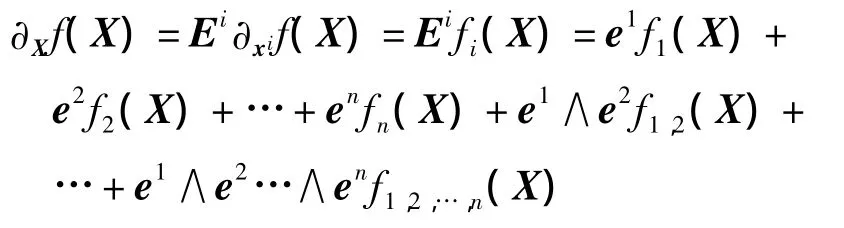
多光谱像素点的光谱Clifford梯度∂Xf(X)的物理意义比较明确，直观上是像素点所有光谱在该处的光谱强度(色度和亮度)的多重矢量函数，综合反映了像素点处任意光谱的强度.

∂Xf(X)是 Clifford代数，多光谱图像的 Clifford梯度范数定义如下:

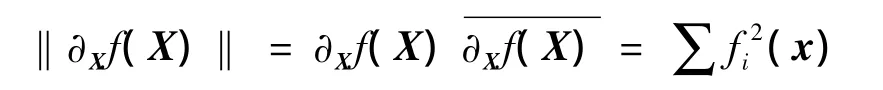
假设输入多光谱图像为Mn×w×h，边缘检测与融合算法的主要步骤如下:

①读取多光谱图像数据M，M为n×w×h的三维矩阵.

②计算多光谱图像在每个像素点处的Clifford代数描述形式.输出为2n×w×h的三维矩阵Mmd.

③ 根据Mmd，计算每个像素点的∂Xf(X)，表现为Clifford多重矢量代数形式.同时，根据梯度范数定义，计算像素点的Clifford梯度范数.输出为多光谱图像梯度范数矩阵Mmf，它是一个2n×w×h的三维矩阵.

④设定数据图像矩阵Mout为2n×w×h的三维矩阵.在Mmf的w×h切面上，根据每个像素点及其周围像素点的均值差异度，判断其是否为边缘点.如果是则将Mout中的对应点置为1;否则置为0.此时可输出多幅边缘检测图像.

⑤对不同w×h切面的二维矩阵数据图像矩阵采用Clifford代数或运算，得到多光谱图像的融合矩阵 Mfusion，即为最终的边缘检测融合图像.Mfusion为w×h的二维矩阵.

3 试验仿真及分析

本文所采用的数据来源于英国UEA大学计算机科学系开发的多光谱图像数据库［15］.多光谱图像光谱范围为400～700 nm，采集步长为10 nm.试验数据中包含31维不同波长的光谱.图1为试验中多光谱图像的原始图及各种边缘检测结果;图2为图1中各图对应的功率谱图.

从图2(a)中可以清楚地看出，多光谱图像数据的频谱图包含31根不同频谱的曲线.所有频谱曲线在高频处都具有峰值，说明在实际图像中灰度剧烈变化，边界明显部分比较多;但在低频处曲线平缓，说明实际图像中含有较多灰度变化平缓的边界模糊部分.

图1(b)和(c)是融合前的边缘检测结果.由图可知，融合前即检测出了部分边缘.图2(b)和(c)为其对应的功率谱图，峰值位置的不一致说明Clifford梯度范数不同阶的边缘检测切片可展现不同的边缘细节.

图1(d)为图1(b)和(c)融合后的边缘检测结果.显而易见，该结果几乎包含了图1(b)和(c)中的所有边缘部分.图2(d)为其对应的功率谱.由图可知，该谱图覆盖了图2(b)和(c)的峰值部分.

由图1(e)可知，本文算法的最终结果包含了大多数边缘信息，说明在多光谱图像边缘检测中基于Clifford梯度的边缘检测与融合算法可以检测出比较理想的边缘信息.图1(f)为利用最大熵边缘检测算法得到的结果，可以看出，与本文算法相比，其检测效果相对较差.原因在于:基于Clifford梯度的边缘检测与融合算法在一定程度上体现了不同波段光谱层之间的关联性，因此在边缘检测时能发现更完整的边缘信息，提高检测精确度.

图2(e)为采用本文算法得到的边缘灰度图的功率谱图.由图可知，高频处峰值明显，说明算法检测出了多光谱图像中比较明显的边界;低频处具有峰值，说明利用该算法可检测出图像中灰度变化不明显的边界.对比图2(e)和(f)后发现，与最大熵边缘检测算法相比，利用本文算法得到的功率谱曲线高频峰值更大、更宽，低频峰值变化更为明显，说明本文算法可检测出比较模糊的边界，从而获得更完整的边缘.

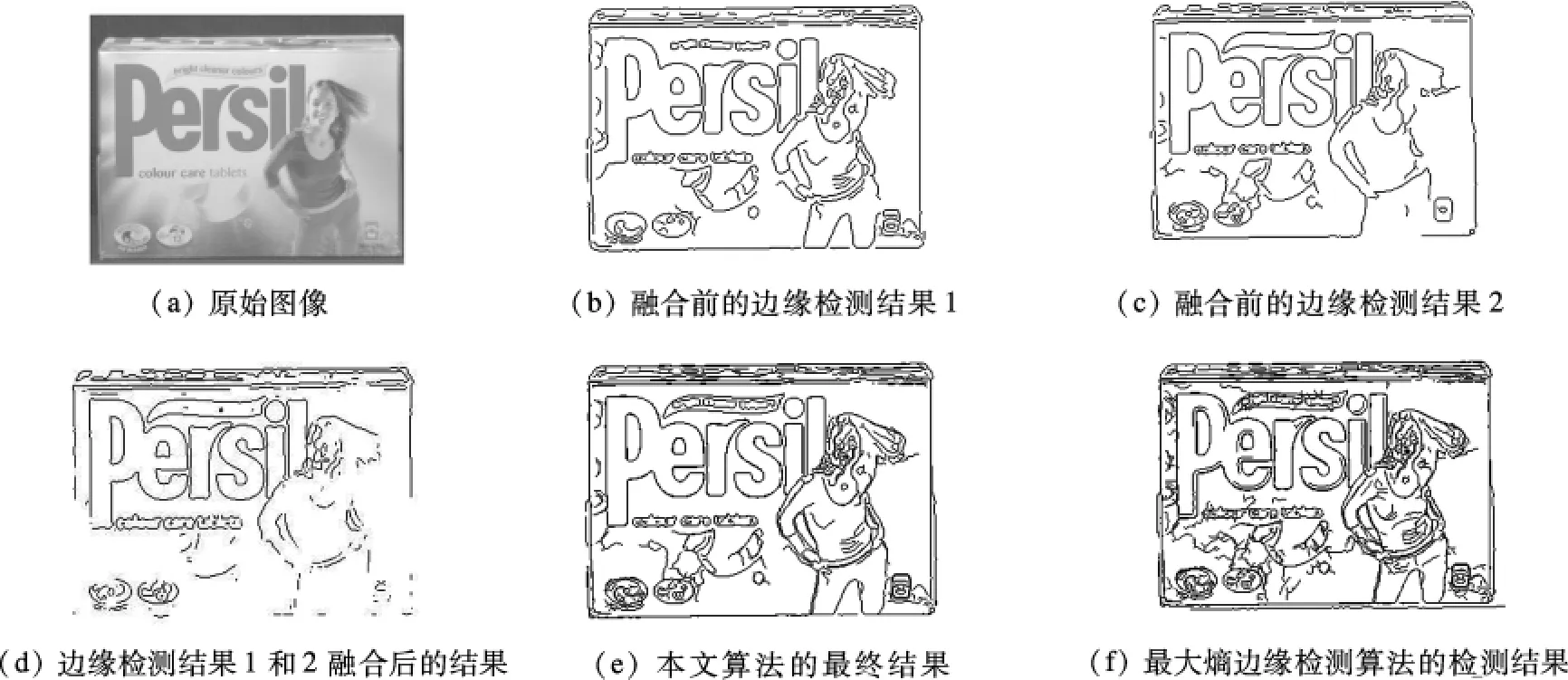
图1 多光谱图像原始图像及边缘检测结果

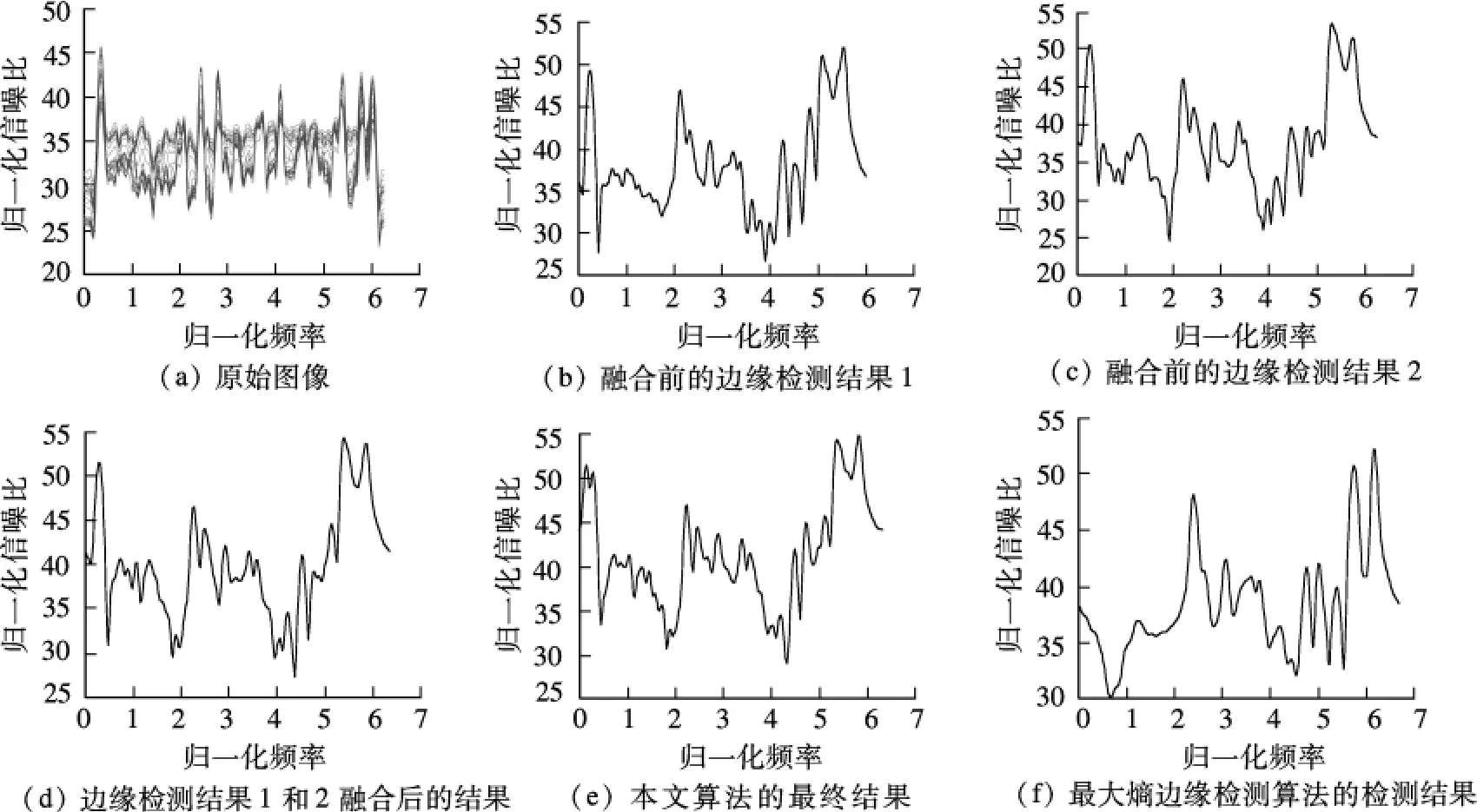
图2 图1中各图像对应的功率谱图

从算法原理和实际运行结果来看，本文算法存在的问题主要是时间和空间复杂度较大.原因在于:多光谱图像的Clifford代数描述方式使得原始图像存储的n维矩阵扩展到2n维，从而导致存储空间指数增长，静态存储空间由原来的O(n×w×h)增加到O(2n×w×h)，同时算法过程中需要的附加堆栈也急速扩充到O(22n×w×h);其次，算法中存在多次多重循环，使得算法时间增加.综合考虑算法②～⑤，得到算法的时间复杂度为O(2n×w×h)，在不考虑w和h的影响时，可以认为算法的复杂度随多光谱图像的光谱分量呈2n级增加.

4 结语

本文采用Clifford代数描述多光谱图像，充分体现了多光谱图像不同图层之间的关联性.通过定义像素点的Clifford梯度来综合反映像素点处光谱的综合强度，并在此基础上提出了一种新型的多光谱图像边缘检测与融合算法.与基于最大熵的多光谱图像边缘检测算法进行比较，结果表明，本文算法可以通过利用不同波段光谱层之间的关联性，识别多光谱图像的模糊边缘，保存更完整的边缘.本文算法存在的问题主要是时间和空间复杂度较大.下一步研究的重点在于如何提高算法效率，同时与同其他算法进行比较，寻找算法的缺陷并继续加以改进.

［1］ Landgrebe D.Information extraction principles and methods for multispectral and hyperspectral image data，information processing for remote sensing［M］.Singapore:World Scientific Publishing Co.，Pte.Ltd.，1999:3-36.

［2］ Mazzoni D，Garay M J，Davies R，et al.An operational MISR pixel classifier using support vector machines［J］.Remote Sensing of Environment，2007，107(1/2):149-158.

［3］ Manian V，Vasquez R.Multiresolution edge detection algorithm applied to SAR images［J］.IEEE Transactions on Geoscience and Remote Sensing Symposium，1999，2:1291-1293.

［4］Rydberg A，Borgefors G.Extracting multispectral edges in satellite images over agricultural fields［C］//Proceedings of1999International Conference on Image Analysis and Processing.Venice，Italy，1999:786-791.

［5］Ruzon M A，Tomasi C.Edge，junction and corner detection using color distributions［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23(11):1281-1295.

［6］Trahanias P E，Venetsanopoulos A N.Color edge detection using vector order statistics［J］.IEEE Transactions on Image Processing，1993，2(2):259-264.

［7］ Economou G，Fotinos A，Fotopoulos S.Color image edge detection based on nonparametric density estimation［C］//Proceedings of2001International ConferenceonImageProcessing. Thessaloniki， Greece，2001:922-925.

［8］Younan N H，Ponnala K，Alapati N.Edge detection in multispectral imagery via maximum entropy［EB/OL］.(2005-08)［2011-10-10］.http://www.isprs.org/publications/related/ISRSE/html/papers/550.pdf.

［9］Theoharatos C，Tsagaris V，Economou G，et al.Edge detection of multispectral images using nonparametric local density estimation［C］//Proceedings of the IASTED International Conference on Signal Processing，Pattern Recognition，and Applications.Rhodes，Greece:ACTA Press，2003:42-47.

［10］徐晨，刘辉，欧阳春娟，等.多光谱图像Clifford拟微分算子及应用［J］.中国科学:信息科学，2011，41(12):1423-1435.

Xu Chen，Liu Hui，Ouyang Chunjuan，et al.Theory and application of Clifford pseudo-differential operator on multispectral image［J］.Scientia Sinica:Informationis，2011，41(12):1423-1435.(in Chinese)

［11］ Batard T，Saint-Jean C，Berthier M.A metric approach to nD images edge detection with Clifford algebras［J］.Journal of Mathematical Imaging and Vision，2009，33(3):296-312.

［12］ Xu C，Liu H，Cao W M，et al.Multispectral image edge detection via Clifford gradient［J］.Sci China Inf Sci，2012，55:260-269.

［13］ Burlakov M P.Clifford structures on manifolds［J］.Journal of Mathematical Sciences，1998，89(3):1311-1333.

［14］曹文明，冯浩.仿生模式识别与信号处理的几何代数方法［M］.北京:科学出版社，2010:84-121.

［15］ Graham F.Multispectral image database［EB/OL］.(2008-07-23)［2011-10-10］.http://www.uea.ac.uk/cmp/research/graphicsvisionspeech/colour/data-code/multispectral-image-db.

Edge detection of multispectral image based on Clifford algebra

Liu Hui Xu Chen Cao Wenming
(College of Information Engineering，Shenzhen University，Shenzhen 518000，China)

In order to make a full use of the connection among different layers of a multispectral image，the Clifford algebra is used to describe the multispectral image.The Clifford derivative and the Clifford gradient of the multispectral image are defined in the Clifford algebra space.Then a new edge detection and fusion algorithm is proposed by analyzing the edge detection and fusion of the multispectral image.In the algorithm，the Clifford gradient for each pixel in the image is computed and the corresponding Clifford normal number is obtained.Whether a pixel is the edge pixel is then judged with the normal number，and several edge detection images are obtained.Finally，the last edge image is deduced by fusing these edge detection images.The comparison results between the proposed algorithm and the edge detection algorithm based on the maximal entropy show that by taking full advantage of the connection among different layers of the multispectral image，the proposed algorithm can keep more integrated edge information of the multispectral image and obtain more complete edges.

multispectral image;edge detection，Clifford algebra;Clifford gradient;image fusion

TP391

A

1001－0505(2012)02-0244-05

10.3969/j.issn.1001 －0505.2012.02.010

2011-09-02.

刘辉(1977—)，男，博士生;曹文明(联系人)，男，博士，教授，wmcao@szu.edu.cn.

国家自然科学基金资助项目(61070087)、深圳市基础基金资助项目(JC201005800305280570A，JC201105080030534011A).

刘辉，徐晨，曹文明.基于Clifford代数的多光谱图像边缘检测［J］.东南大学学报:自然科学版，2012，42(2):244-248.［doi:10.3969/j.issn.1001 －0505.2012.02.010］