一种基于遗传算法求解TSP问题的优化算法

韩凤娇

西南大学计算机与信息科学学院 重庆 400715

0 引言

旅行商问题是经典组合优化问题，也是一个NP完全问题。它的求解会随着问题规模扩大而导致求解时间急速增长。为此我们可以利用遗传算法这一智能的算法，来试图获得问题的较优解，并通过反复改进实验最终寻求较快较优解决方法。

TSP即旅行商问题或称货郎担问题，该问题描述为：有n个城镇，其中任意两个城镇间都有道路(若没有则规定该边上的权值为+∞)。一个售货员要去这n个城镇售货，从某城镇出发，一次访问其余n-1个城镇且每个城镇只能访问一次，最后又回到原出发地。问售货员要如何安排经过n个城镇的行走路线才能使他走过的路程最短。

求解旅行商问题，其实质是在一个赋权图中寻找一条权值最小的哈密尔顿回路。哈密尔顿回路是指：有任意图G=(V，E)，G中进过所有节点一次且仅一次(除起点重复一次)的圈。从中也可以看出，旅行商问题是一个最优化的求解问题，它要求问题的解满足以下三点：(1)它必须是一条回路；(2)该回路能够经过每个事先给出的城镇且不重复访问已经过的城镇；(3)回路的路径长度是所有可以满足(1)、(2)的若干回路中最短的。

1 遗传算法介绍

遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存，优胜劣汰遗传机制)演化而来的随机化搜索方法。它是由美国的J.Holland教授1975年首先提出，已被人们广泛地应用于组合优化、机器学习、信号处理和人工生命等领域。

遗传算法的基本运算过程如下：

(1) 编码：针对要求解的问题，对可能的解用数串等方式进行编码，如二进制串等；

(2) 初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成N个体作为初始群体P(0)；

(3) 适应性评价：计算群体P(t)中每个个体的适应度，为其后的选择、交叉、变异做准备；

(4) 选择操作：将选择算子作用于群体。从而把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代；

(5) 交叉操作：将交叉算子作用于群体。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作，这是遗传算法的核心；

(6) 变异操作：将变异算子作用于群体。即是对群体中的个体串的某些基因位置上的基因值作变动；群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。

(7) 终止条件判断：若t=T，则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

从上述可知，当城镇数量增加，问题规模扩大时，将难以在有限的时间内保证得到旅行商问题的最优解。然而，在实际应用中，我们若是无法得到最优的结果，往往希望得到一个较优的结果来代替它。因此，我们最终希望能够在城镇数量为50或以上的问题中得到良好的结果。

2 遗传编码与种群初始化

利用遗传算法求解问题，我们先将城镇从1开始顺序编号，以此作为一个单独的元素，利用一个长度等于城镇数量n且元素两两不同的数字串表示一条回路进行染色体编码。对于路径A1A2A3……An-2An-1An表示依次经过城镇A1、A2、A3……An-2、An-1、An最后由An回到始点A1。在所使用的实验平台MATLAB中，提供了一个极其有效的函数randperm(n)，该函数能够产生一个n个元素的排列，恰好与我们的编码方式对应。

另外，为了保持初试种群的多样性，我们可以将初始种群的染色体数量控制在问题规模n与2n之间。

2.1 适应性函数

适应性函数值是评价一个染色体好坏的依据，具有良好适应性的染色体应当在遗传过程中具有更高的存活能力。就该问题而言，由于TSP要求得到一条路径较短的回路，那么路径长度较短的回路应该具有更高的适应性，存在负相关。为此，我们可以将路径的倒数作为适应性函数值，也就是令染色体x的适应性函数为， RouteLength表示回路的长度：

2.2 选择算子

计算完各染色体的适应性之后，就应当以它们的适应性函数值为依据对染色体进行选择。在这里，我们选常用的轮赌选择方法。比率的计算公式如下：

其中，r(xi)为第i个染色体的比率，f(xi)为第i个染色体的适应性函数值，n为种群染色体总数。染色体适应性越好，比率越大，被选中的概率也就越大。由以上公式得到的回路适应性比率可以构成一个总和为 100%的轮盘，通过轮盘指针旋转确定所选染色体。若指针取值属于区间(0，1)且上述示例对应轮盘图1所示，则可以方便的确认当下指针所对应该选取的染色体。

图1 回路适应性比率

例如，当指针取值为0.8时，由于71.99% < 0.8 = 80% <84.86%，因而该取染色体4。

2.3 交叉算子

交叉操作一般分为如下几个步骤：

(1) 从待交配的种群中选取要交配的一对个体；

(2) 根据位串长度 L，对要交配的一对个体随机选取一个或多个交叉位置；

(3) 根据交叉概率pc实施交叉操作，配对个体在交叉位置处互相交换各自的部分内容，之后按照实际问题适当调整，形成一对新个体。

通常使用的遗传算子又包括一点交叉、两点交叉、多点交叉、一致交叉，这里我们选择一种一点交叉的方式来完成该步操作。以下我们举例说明这种交叉方式，为方便理解，选取路径长度(城镇个数)为 8，交叉的两个元素分别加以标记，具体操作如表1所示。

表1 交叉操作示例

2.4 变异算子

变异是遗传算法的又一必要操作，也是保持种群多样性的有效手段。当然，变异在遗传过程中并不是经常出现的，因而变异概率pm一般取的很小。

对于TSP，染色体的变异与之前的交叉操作类似，某个元素的改变(变为与自身不相等的另一个元素)必然无法保持回路特性，因而需要进行调整。例如，染色体1-2-3-4-5-6-7-8在第6位发生变异，不妨设由元素2取代它看，之

3 实例解析

由于城镇数量太大，会因染色体过长而导致问题求解过程的叙述过于冗长，不利于直观的理解。而问题规模的大小对算法的思想并没有直接的影响，故在此仅以一个 10城镇的无向图作为例子进行求解。通过分析城镇数，我们产生一个邻接矩阵D如下所示：

在此我们选择交叉概率pc=0.8，变异概率pm=0.005，初始种群大小为20，而迭代次数定为200次。

3.1 初始化实例种群

通过相应的函数我们可以得到一个大小为 20的初始化种群，在TSP问题中每条回路的路径长度等于回路各边权值的总和，例如任意一条回路 i1-i2-i3-i4-i5-i6-i7-i8-i9-i10，路径长度dtotal对应的数学表达式为：

针对第一条路径 1-5-6-4-7-9-8-2-3-10，它的路径长度dtotal=8+44+12+16+70+76+75+25+4+53 =383。以此类推，我们可以得到各个染色体的适应性。

3.2 选择染色体

该步骤中，利用函数rand随机生成0到1内的数据，根据轮盘算法原理，重复20次后可以得到第1代种群。

将种群中两两配对在既定的交叉概率下进行交叉操作，即染色体1与2配对，3与4配对……依此类推，若种群中染色体个数为奇数，则最后一个染色体保留。经过此操作，我们可以得到第一代染色体交叉后的结果。

3.3 种群变异

首先确定一个要变异的位置P1，之后随机生成一个与该位置上元素不同的另一元素E，找到元素E的位置P2，最后交换P1、P2上的元素。例如，4-7-3-8-1-9-10-6-2-5选取了位置 P1为9，随机产生的元素E为7对应位置P2为2，标记后的位串此操作，我们可以得到第一代染色体变异后的结果。

3.4 实例运算结果

依照以上步骤迭代指定次数后，最终得到路径为6-5-1-10-9-3-2-7-8-4，路径长度为214。对该实例重复运算多次后，偶尔有路径长度212的回路出现，但概率较低，从而可以认定该结果为一个较优解。此外，我们在程序中还设置了最小路径长度向量及平均路径长度向量分别记录每次迭代中的最短和平局路径长度，由此绘制出平均路径长度与最短路径长度随迭代次数变化的曲线如图2。

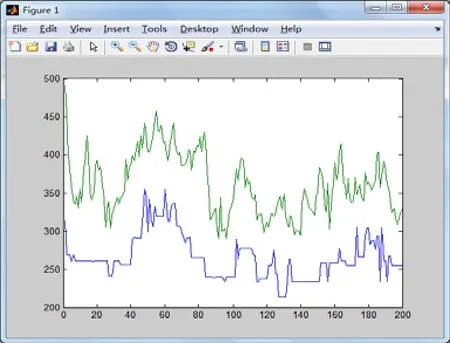
图2 路径长度随迭代次数变化曲线

由上面的变化曲线图我们可以看到，迭代过程中最小和平均路径长度函数曲线却表现出一种不稳定性，其波动显示该算法的求解存在一定的瑕疵。当城镇数量增加时，能否得到较优解还未定。

4 算法分析与改进

为更有效的、更直接的评价之前的算法，我们将问题规模扩大，将城镇数量增大到最初预想的50个。对于已经生成的邻接矩阵，设定迭代次数800，交叉概率pc为0.8，变异概率pm为0.005，种群大小为75。最终求得一个解回路为：19-48-50-44-25-41-15-11-28-42-35-12-26-22-32-9-37-4-20-36-8-46-38-40-43-27-29-45-2-24-17-39-1-18-7-30-31-14-21-3-16-5-10-49-34-23-13-47-33-6，对应的路径长度为1555。

利用路径长度的倒数作为适应性函数能够解决适应性与路径长度负相关的问题。可路径长度一般较长，尤其是问题规模扩大时，不同的路径长度所对应的适应性函数值部分过大部分过小，最后导致轮赌选择时个别不同染色体被选取的可能性相差甚远。

任意一个种群的各个路径长度中，必然存在最大值与最小值，于是考虑让路径长度最短的回路取得适应性为 1，而最长的回路取得适应性为0，其他回路则介于0和1之间。那么得到新的适应性函数为：

再来看之前的例子，适应性依次为：1、0.75、0.5、0.25、0，被选概率为 40%、30%、20%、10%和 0%。表现出线性递减的特性，并且淘汰了路径长度最长的回路。再次运行程序查看性能图(如图3所示)。

图3 引入最值的适应性函数的性能图

该图像中有一明显的向下尖峰，且较之前有更多最小路径长度点位于1800以下，就此决定选用该函数为新的适应性函数。

5 利用遗传算法求解TSP的注意点

遗传算法借鉴了生物遗传的思想，选择、交叉、变异就是遗传算法的关键所在，其中尤以交叉操作影响最大。若是交叉方式不当，导致迭代结果无法收敛，则会使算法陷入僵局，算法也就失去了意义。这也意味着，交叉算子的选取是重中之重！

在利用遗传算法求解TSP并对其分析改进后，在此总结出如下注意点：

(1) 选择良好的适应性函数。适应性的好坏，本质上是由回路自身决定的，如何恰如其分的量化这种优劣程度，使其具有较好的区分度是一个适应性函数所必备的性质；

(2) 必须使用收敛的交叉算子。研究者无论是利用该算法求解还是进一步改进，在设计交叉操作时，若不能保证算子收敛，很有可能导致求解功亏一篑；

(3) 保证一定的种群多样性。种群多样性的存在，能够帮助在交叉等操作中得到更优的子代，从而突显出遗传算法的价值。

总之，要利用遗传算法求解TSP，必须在掌握基础理论及操作的基础上，尽量保持原有的优良性征，恰当评价，合理改进算子，保证算法收敛。

6 结论

本次研究过程中，通过对遗传算法核心思想的思考，在解决TSP问题上得到了启发。因为最初适应性函数及交叉算子选取不当，导致在选择操作和交叉操作分别出现无法合理区分和无法有效收敛的现象。此后，一方面通过改进适应性函数，增加区分度加强了选择的有效性；另一方面利用改进顺序交叉算子并大胆采用淘汰机制，保证并加快了收敛能力。最终通过几方面的结合，改进原有算法，达到了有限时间内求取较优解目的。

[1]毕晓君.信息智能处理技术[M].北京:电子工业出版社.2010.

[2]邓辉文.离散数学[M].北京:清华大学出版社.2006.

[3]任春玉.基于混合遗传算法的TSP问题优化研究[J].哈尔滨商业大学学报.2007.

[4]Negnevistsky,M.顾力栩,沈晋惠译.人工智能——智能系统指南[M].北京:机械工业出版社.2010.

[5]刘雁兵,刘付显.基于遗传算法的 TSP问题求解与仿真[J].电光与控制.2007.

[6]张春霞,王蕊.基于遗传算法求解 TSP问题的算法设计[J].安阳工学院学报.2007.

[7]郑阿奇.MATLAB实用教程[M].北京:电子工业出版社.2004.

[8]李飞,白艳萍.用遗传算法求解旅行商问题[J].中北大学学报.2007.

[9]刘青凤,李敏.基于遗传算法的TSP问题优化求解[J].计算机与现代化.2008.

[10]翟梅梅.基于交叉算子改进的遗传算法求解 TSP问题[J].淮南师范学院学报.2009.

[11]邢桂华.用MATLAB实现中国旅行商问题的求解[J].微计算机应用.2004.

[12]周涛.基于改进遗传算法的 TSP问题研究[J].微电子学与计算机.2004.

[13]Merz P.A comparison of memetic recombination operators for the traveling salesman problem[A].Proceedings of the Genetic and Evolutionary Computation Conference(GECCO).2002.