目标垂深和造斜率不确定条件下的水平井轨迹设计

孙腾飞，高德利，张 辉，梁奇敏

(中国石油大学，北京 102249)

目标垂深和造斜率不确定条件下的水平井轨迹设计

孙腾飞，高德利，张 辉，梁奇敏

(中国石油大学，北京 102249)

在水平井钻井中普遍存在工具造斜率和目标垂深不准确的现象，这使水平井井眼准确进入目标窗口的难度大大增加，甚至导致脱靶。由此提出了解决该问题的方法，研究表明:采用双增型水平井设计出中间稳斜段的最佳稳斜角，在钻进中及时发现标志层或油层顶界面等方法，可以解决目标垂深和造斜率不准确的问题。考虑了标志层的倾角和储层倾角不平行的情况，并推导了整套设计的计算公式，并通过实例验证了标志层倾角的重要性。

水平井;目标垂深;不确定;轨迹设计;双增剖面

引言

水平井钻井技术是在定向井技术基础上发展起来的一项钻井技术。水平井具有扩大油气层裸露面积、提高油气井单井产量、提高油气采收率等特点，对于薄层油气藏、高压低渗透油气藏等特殊油气藏水平井具有很好的开发效果［1］。水平井轨迹设计的准确与否十分关键，通常水平井轨迹的基本形状有2种类型，一种是单增轨迹，由“直—增—平”三段组成，另一种是双增轨迹，由直井段、第1增斜段、稳斜段、第2增斜段和水平段组成，其突出特点是在两段增斜段之间设计了一段稳斜调整段，以调整目标垂深误差造成的轨道偏离。在使用导向钻井系统的中、长半径水平井中，常会遇到造斜率准确而目标垂深不准确的情况［2－7］。本文对此情况下的轨迹计算方法进行优化。

1 基本思路

文献［8－9］在造斜率、目标垂深都不准确的情况下阐述了水平井轨迹设计的思路和方法，本文采用该设计思路，对其设计方法进行了完善和修正。

2 轨迹设计

2.1 轨迹设计过程推导

根据参考文献［2］，在造斜率和目标垂深都不确定的条件下(图1)，中间稳斜段的最优井斜角公式如下［10］:

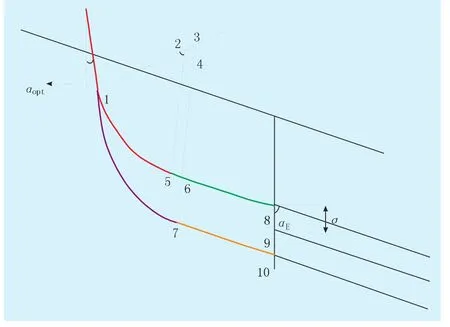
图1 不确定条件下的轨迹设计

式中:αopt为中间稳斜段最优井斜角，(°);αE为储层倾角，(°);σ为窗口的半高度，m;kmin为工具的最小造斜率，0.03°/m;kmax为工具的最大造斜率，0.03°/m。

2.2 轨迹设计修正

通过研究发现以上模型有一定的不足，因为其推导过程是建立在从第2造斜段开始分别以最大和最小造斜率为轨迹上下界的，忽视了其实在第1造斜段也会有工具造斜率的不确定性，同时以上的推导认为标志层和储层是平行的而没有考虑不平行的情况，因此对轨迹的设计推导进行了改进，改进后的轨迹设计示意图如图2所示。

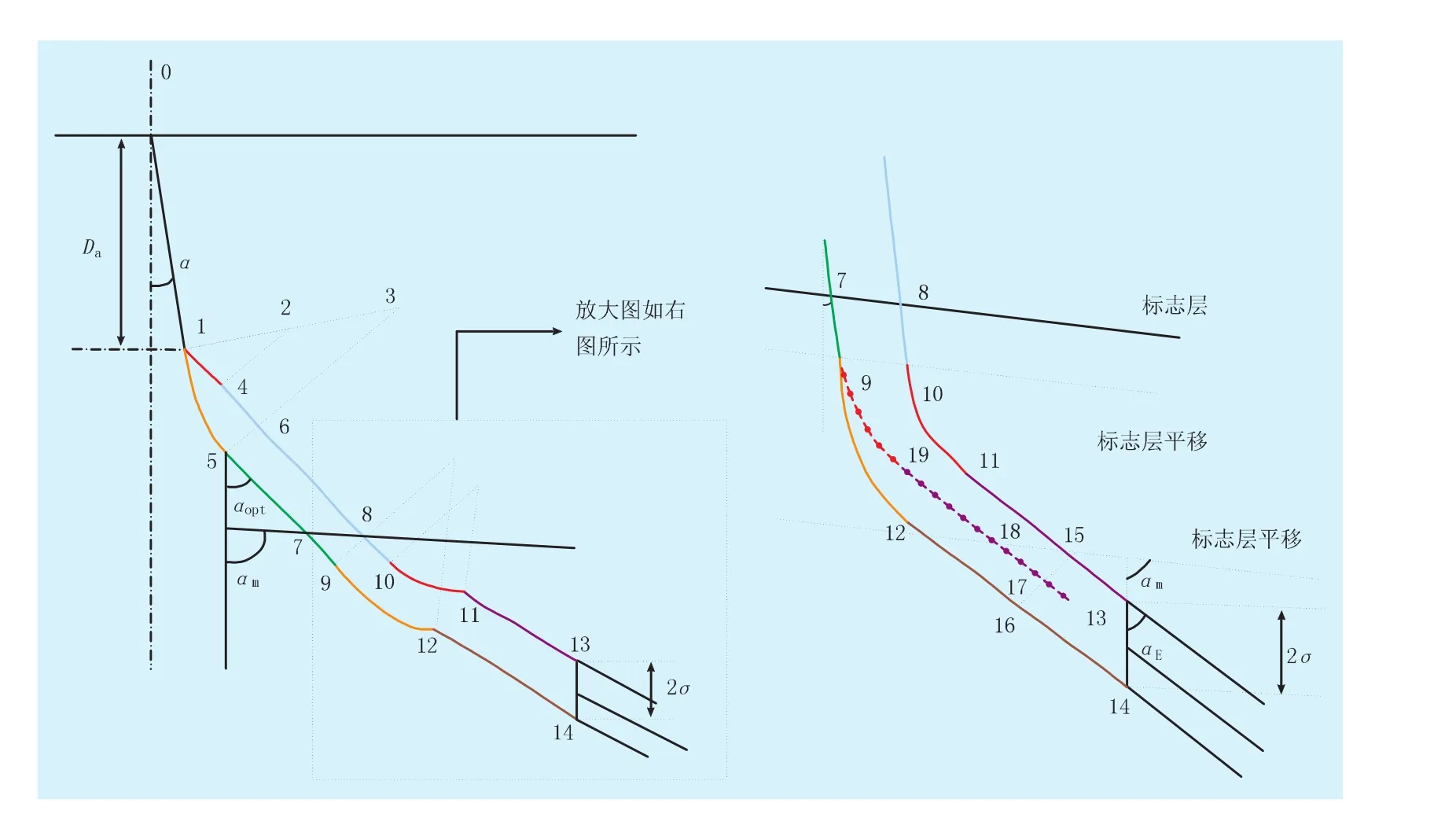
图2 不确定条件下的轨迹修正设计

将l10，11，15，13沿着 l9，10方向整体平移，将最大造斜率时轨道和第2造斜段的起点平移到与最小造斜率时轨道第2造斜段的起点重合的位置，因此可以得到:

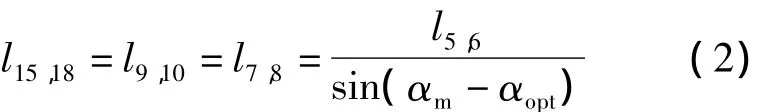
根据几何关系 l5，6=l3，5－l2，4－l2，3cos(αoptαa)可以得到:

又因为l15，18=l5，6/sin(αm－αopt)，所以:

根据式(3)的推导方法可以得到:

因为l15，17=l15，18sin(αm－αE)，所以:

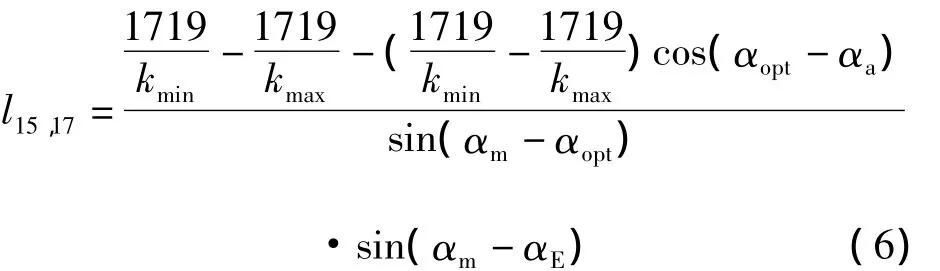
由l15，16=l16，17+l15，17，可得:

式中:αopt为未知的稳斜段井斜角，(°);αm为标志层的倾角，(°);αE为储层的倾角，(°)。

根据式(9)可以求得在目标垂深和造斜率都不确定条件下的最优切线段稳斜角αopt的大小。

当目标垂深滞后，采用最小和最大造斜率分别进入滞后窗口的下界和上界，此时的滑行段为0，根据图3可以得到如下计算公式:t

图3 轨迹设计示意图

式中:Da为第1造斜点的垂深，m;Se为水平位移，m;l4，10为上界轨迹中间稳斜段长度，m;l5，9为下界轨迹中间稳斜段长度，m。4个方程4个未知数，因此可以求得2个关键参数Da和Se。

再根据图4，当第1和第2造斜段的预期造斜率分别为k1和k2时，可以得到以下关系式:

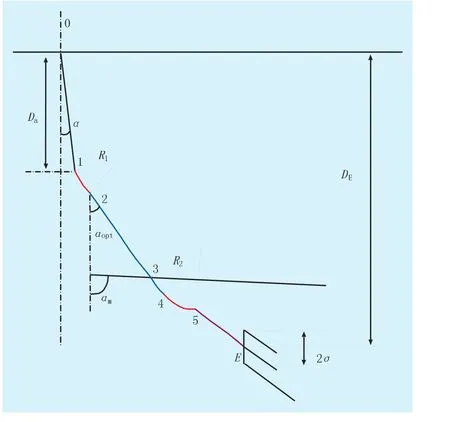
图4 轨迹设计示意图

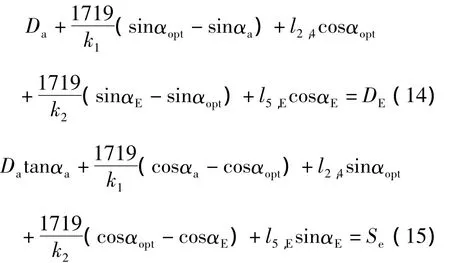
根据式(10)～(13)得到的Da和Se，联立式(14)和(15)可以得到所需要的参数l2，4(中间稳斜段长度)和l5，E(滑行段长度)。

至此，已经得到了在造斜率和目标垂深不确定条件下的轨迹设计的关键参数:最优切线段稳斜角αopt，中间稳斜段长度l2，4和滑行段长度l5，E。

3 算例

一口水平井进行双增型水平井井眼轨迹设计时的设计参数为:目标井斜角αE=85°，造斜工具最小造斜率 kmin=0.26°/m，最大造斜率 kmax= 0.40°/m。由于地质情况比较复杂，预计的目标窗口中心的垂深HE=2 100 m，因目标垂深的不确定性，因此最小可能垂深HE'=2 093.7 m，最大可能垂深HE″=2 106.3 m，储层厚度σ=4 m。为了能够精确中靶，根据式(9)计算得到了最优进入角的计算结果为αopt=57.7°。但在实际钻井过程中，根据实测结果发现目标储层与标志层的倾角相差了1°，即αm=86°，结果导致采用最初设计的最优稳斜角设计方案时不能精确中靶。经过重新计算调整，当最优稳斜角为αopt=60.38°时，可以精确中靶。因此从实际结果上可以看出，当标志层与储层的倾角只相差1°时，最优稳斜段的井斜角相差了将近3°，因此储层和标志层的倾角是否相同十分关键，这对准确进入目标窗口有着十分重要的作用。

4 结 论

(1)采用双增型水平井设计出中间稳斜段的最佳稳斜角，在钻进中及时发现标志层或油层顶界面等方法，可以解决目标垂深和造斜率不准确的问题。

(2)在前人研究的基础上，考虑了第1和第2造斜段造斜率不确定性以及标志层倾角和储层倾角不平行的情况对最优稳斜角的影响，推导出了适应性更强的最优稳斜角计算公式。

(3)储层和标志层的倾角是否相同十分关键，这对准确进入目标窗口有着十分重要的作用。

［1］Karlsson H，et al.New developments in Short－Medium－and Long－Radius lateral drilling［R］.SPE/IADC Drilling Conference，1989:87－98.

［2］刘修善，石在虹.水平井轨道实用设计方法［J］.石油钻采工艺，1994，16(1):5－8.

［3］韩志勇.双增形水平井轨道的设计［J］.石油大学学报:自然科学版，1991，15(4):15－20.

［4］高兴坤，等.胜利油田常见二维水平井轨道设计［J］.石油钻探技术，1997，25(2):9－11.

［5］徐德行.水平井地质设计中着陆点和断点确定技术研究［J］.内蒙古石油化工，2011，37(6):92－94.

［6］任志杰.中曲率水平井入靶设计与控制技术［J］.特种油气藏，2006，13(5):82－84.

［7］佟长海.井身轨道设计的优化计算方法［J］.特种油气藏，2005，12(1):60－62.

［8］韩志勇.两个不准确条件下的水平井轨道设计［J］.石油大学学报:自然科学版，1993，17(1):24－30.

［9］苏义脑.水平井井眼轨道控制［M］.北京:石油工业出版社，2000:172－197.

［10］韩志勇.定向钻井设计与计算［M］.东营:中国石油大学出版社，2007:145－148.

编辑 张耀星

TE319

A

1006－6535(2012)04－0141－04

10.3969/j.issn.1006－6535.2012.04.036

20120209;改回日期:20120320

国家科技重大专项“复杂结构井轨迹设计与控制一体化”(2011ZX05009－005);国家自然科学基金项目“气体钻井井眼轨迹偏斜机理与控制理论研究”(51174220)

孙腾飞(1986－)，男，2008年毕业于中国石油大学(华东)石油工程专业，现为中国石油大学(北京)油气井工程专业在读博士研究生，从事复杂结构井眼轨迹设计与控制一体化方面的研究。