基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法

彭 畅，柏 林，谢小亮

(重庆大学 机械传动国家重点实验室，重庆 400030)

滚动轴承是旋转机械中应用最广泛的关键零部件，其工作状态直接影响整台机器运行效率和使用寿命。由于滚动轴承承受冲击的能力差，也是机器中最易损零件，因此对于滚动轴承的状态监测和故障诊断具有十分重要的现实意义。

Huang等[1]提出的EMD(经验模式分解)方法的主要思想是把一般的时间序列信号分解成一系列的IMF(本征模函数)，由于该方法具有直观、直接、后验、自适应的优点，并且能处理非稳态和非线性数据[2]，故在信号处理领域得到了广泛的应用。谱峭度用统计量检测含噪信号中的瞬态成分，其概念最早由Dwyer[3]提出，Antoni等[4－6]系统的定义了谱峭度，并先后提出了基于STFT(短时傅里叶变换)的谱峭度法及谱峭度图的快速算法，并将其应用到旋转机械的监测和故障诊断中验证了该方法的有效性。此后有学者将EMD和谱峭度法联合引入到滚动轴承故障诊断应用中，苏文胜[7]结合EMD降噪作用和谱峭度的滤波器功能更好地诊断出了滚动轴承的早期故障，蔡艳平[8]提出的将EMD、谱峭度和包络法相结合的滚动轴承故障诊断方法克服了传统的包络分析法中主观性的影响，具有更好的分析结果。

1 基本算法

在以上研究成果的基础上，本文提出了改进的基于EEMD(总体平均经验模式分解)和快速峭度图的滚动轴承故障诊断方法，该方法是将EEMD、相似性度量以及快速峭度图相结合的一种改进方法。

1.1 EEMD算法

为了克服传统EMD产生的模式混叠现象，Wu等[9]提出了利用白噪声的总体平均经验模式分解(EEMD)算法。EEMD本质上是一种噪声辅助信号处理方法，它通过多次给待分析信号加入零均值但不同有限幅值的高斯白噪声，利用高斯白噪声的频率均匀分布统计特性改变信号的极值分布特性使得信号在整个频带中的极值点间隔分布均匀，克服了极值点上下包络线的拟合误差，然后再对多次分解的IMF进行总体平均，从而获得了既能避免模式混叠现象又准确的并消除了噪声加入影响的本征模函数。文献[9]中给出的EEMD的具体算法如下:

(1)给分析信号加入白噪声序列;

(2)将加入了白噪声的信号分解成各IMFs;

(3)重复步骤(1)和步骤(2)，但是每次都加入不同的白噪声序列;

(4)求分解得到对应IMFs的总体平均，并将平均之后的IMF序列作为最终的结果。

1.2 度量因子

1.2.1 相似性度量[10]

聚类分析是数据挖掘领域中非常重要的研究课题，它的目标就是在相似的基础上利用数学方法研究和处理给定对象的分类。相似性度量作为聚类分析中的子概念，是用来度量样本之间的相似性的，由于度量的样本类型不同又分为距离和相似系数两种不同定义，本文根据信号数据的时序特性选取距离作为度量因子，其中距离的具体定义如下。

把n个样品看成是m维空间中的n个点，两个样品间的相似度用 di，j度量。di，j为样品 Xi，Xj的距离，距离 di，j须满足四个条件:

(1)对于任意的i，j;

(2)当 di，j=0⇔X(i)=X(j);

(3)对任意i，j满足;

(4)di，j≤di，k+dk，j，对于任意 i，j，k。

距离有多种定义方法，常用的有欧式距离，其计算公式为:

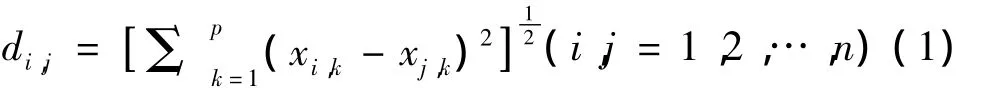
1.2.2 基于距离的度量因子

将故障信号X(fault signal)进行EEMD分解后得到一组IMFs记为C1，C2，…，Cm，不同的 IMF与原始故障信号的相关程度不同，因此在对IMF进行后续分析之前需要将最敏感的IMF分量选择出来。因此提出了一种使用基于距离的度量因子来评估IMF分量与原始信号相似程度的算法。该算法可表述为首先计算原始故障信号与本征模函数分量之间的距离，并将其定义为评估每个IMF分量的度量因子Ri，然后比较所有度量因子Ri的值，最后选取Ri值最小或次小的IMF用来表征故障特征。设故障信号的采样点数为N，则度量因子Ri的数学表达式为:

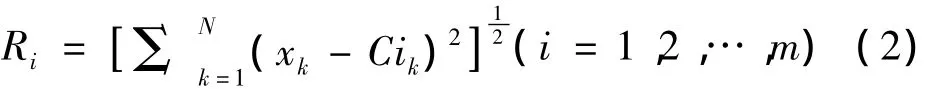
1.3 谱峭度及快速峭度图

1.3.1 谱峭度定义

Antoni对谱峭度进行了深入的研究，在文献[4－5]中详细阐述了基于谱峭度的理论基础，正式给出了谱峭度的数学定义，并将其成功应用到旋转机械的故障诊断中。在非平稳情况下，定义Y(t)为由信号x(t)激励的系统响应，其 Wold-cramer分解的频域表达式为:

式中:H(t，f)是系统的时变传递函数，表示Y(t)在频率f处的复包络。

定义Y(t)的四阶谱累计量为:

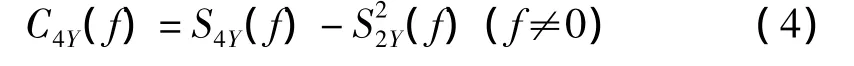
式中:S2nY(f)是谱瞬时距，用来度量复包络能量，定义为:

将谱峭度定义为归一化累计量表示为:

1.3.2 快速峭度图

文献[4－5]中为了获取基于谱峭度的最优滤波器的参数，将谱峭度作为STFT窗口宽度的函数提出了峭度图的概念。由于计算中心频率和STFT窗口所有组合的峭度图费时又不便于工程实践的应用，文献[6]进一步提出了快速峭度图的概念。在原理上类似于离散小波包分解的快速算法，能够得到与峭度图同一水平的结果但是计算时间显著减少。在二维快速峭度图像中横坐标代表频率f，纵坐标则表示分解的层数K，频率分辨率Δf=2－(K+1)fs，图像上的颜色深浅表示不同f和Δf下的 SK值[7]。本文采用快速峭度图计算出来的最大SK值所对应的f和Δf作为检测滤波器的参数。

2 改进的故障诊断方法流程

本文改进的故障诊断方法中所使用的EEMD算法不仅完全继承了EMD算法的优点即能将信号自适应地分解到不同的尺度上，适合于非线性、非平稳信号的处理，可广泛应用于工程领域，而且EEMD还很好地克服了EMD中的模式混叠问题，使最终分解得到的IMFs更加精确。此外，本文提出了基于距离的度量因子的概念，将其用于评估各IMF分量与原始故障信号的相关性，从而筛选出能够更好地表征故障信息的IMF分量。用快速峭度图算法准确迅速确定带通滤波器的中心频率及带宽。将EEMD、相似性度量、快速峭度图与包络分析相结合有望取得满意的故障诊断结论。改进的故障诊断方法的流程图如图1所示，具体步骤表述为:

图1 故障诊断流程图Fig.1 Flow chart of fault diagnosis

(1)对故障信号进行EEMD分解得到m组IMFs;

(2)计算每个IMF的度量因子Ri;

(3)筛选出度量因子Ri最小或次小的IMF进行信号重构;

(4)计算重构信号的快速峭度图，将谱峭度值最大处对应的中心频率fc和带宽Bw作为带通滤波器的参数;

(5)对重构信号进行滤波之后作包络分析;

(6)利用最终获得的包络谱与滚动轴承故障特征频率进行故障诊断。

3 改进算法的应用

3.1 仿真数据验证

首先用Ho等[11]提出的仿真滚动轴承故障模型数据验证改进算法的有效性。根据文献[11]仿真的滚动轴承内圈故障信号如图2所示，它是用单自由度弹簧－质量－阻尼系统仿真滚动轴承内圈故障时的冲击响应，并混入信噪比为5的高斯白噪声而产生的。仿真故障信号的故障特征频率为100 Hz，调制频率为3 kHz，采样频率为50 kHz。① 对该信号进行 EEMD分解得到12组IMF分量，如图3所示。② 分别计算各IMF分量与原始故障信号的度量因子Ri，见表1。根据度量因子的概念可知度量因子的值越小其所对应的IMF分量与原始信号的相关程度越大，越能表征故障信息，因此选取Ri的最小值所对应的本征模函数分量C1重构信号，如图5(a)所示。③ 计算重构信号的快速峭度图(如图4)得到一组最优滤波器参数。④ 对重构信号进行带通滤波并进行包络分析，得到的包络谱如图5(b)所示。从平方包络谱图中可以清楚地看到故障频率98.43 Hz及其倍频，因此仿真数据的诊断结果很好地验证了本文所提改进算法的有效性。

图2 仿真的滚动轴承内圈故障信号Fig.2 Simulated fault signal of rolling bearing’s inner race

图3 仿真信号EEMD分解结果Fig.3 EEMD result of simulated signal

图4 快速峭度图Fig.4 The fast kurtogram

图5 重构信号及其平方包络谱Fig.5 Reconstructed signal and it’s squared envelope spectrum

表1 各IMF分量的度量因子Tab.1 Measure-factor of each IMF

3.2 工程应用

为了进一步检验改进算法在实际的旋转机械滚动轴承故障诊断应用中的有效性，本文选取美国Case Western Reserve University公开的轴承故障数据[12]进行内圈故障诊断。根据Drive end bearing(12 k)中代号为IR007_1的故障数据可知轴的转速n=1 772 r/min(fr=29.53 Hz)，采样频率 fs=12 000 Hz，由轴承参数计算得到的内圈故障特征频率f1=159.9 Hz。

按图1对上述实测数据进行诊断，先将原始信号进行EEMD分解得到15组IMFs，计算各自的度量因子Ri，对IMFs进行筛选并重构信号，计算其快速峭度图并构造带通滤波器，再对滤波后的重构信号进行包络分析得到平方包络谱图。篇幅所限只给出实测故障信号图(如图6所示)以及平方包络谱图(如图7所示)，从图7(b)中可以清晰地看到故障频率为159.8 Hz及其倍频，从而很好地验证了本文所提出的改进算法能够有效地应用到实际的旋转机械滚动轴承故障诊断中，需要说明的是包络谱中其他频率成分是由于引用的数据中混合了轴承其他故障类型所致。

图6 实测轴承内圈故障信号Fig.6 Fault signal for factual rolling bearing inner race

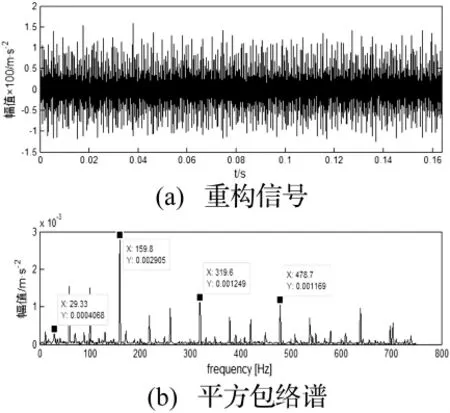
图7 实测信号的重构信号及其包络谱Fig.7 Reconstructed signal and squared envelope spectrum of factual signal

4 结论

针对本文提出改进的基于EEMD和快速峭度图的滚动轴承故障诊断方法的特点进行分析如下:

(1)改进算法中使用EEMD代替传统的EMD，不仅很好的继承了EMD能够将包括非线性非平稳信号自适应分解到不同时间尺度上的优点，而且克服了EMD可能产生的模式混叠现象，使得最终分解得到IMF分量能够更加准确地表征故障特征。

(2)根据相似性度量理论提出的基于距离的度量因子作为评估IMF分量与原始信号相似程度的参数，能够有效地筛选出最有效的IMF分量用于信号的重构。

(3)快速峭度图算法快速、准确能够自动选择带通滤波器参数，大大简化了传统的滤波器构造过程，更加实用准确。

(4)改进的基于EEMD和快速峭度图的滚动轴承故障诊断方法在旋转机械故障诊断领域具有良好的应用前景。

[1]Huang N E，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J].Proc.R.Soc，1998，454:903－ 905.

[2]诸福磊，彭志科，冯玉鹏，等.机械故障诊断中的现代信号处理方法[M].北京:科学出版社，2009:115－121.

[3]Dwyer R F.Detection of non-Gaussian signals by frequency domain kurtosis estimation [C].Acoustic，Speech and Signal Processing.Boston:IEEE Inter-national Conference on ICASSP，1983:607－610.

[4]Antoni J，Randall R B.The spectral kurtosis:a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing，2006，20(2):282 －307.

[5]Antoni J，Randall R B.The spectral kurtosis:application to the vibratory surveillance and diagnostics of rotating machines[J].Mechanical Systems and Signal Processing，2006，20(2):308－331.

[6]Antoni J.Fast computation of the Kurtogram for the detection of transient faults[J].Mechanical Systems and Signal Processing，2007，21(1):108－124.

[7]苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击，2010，29(3):18－21.

[8]蔡艳平，李艾华，石林锁，等.基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J].振动与冲击，2011，30(2):167－172.

[9]WuZ H， HuangN E. Ensemble empiricalmode decomposition-A noise assisted data analysis method [J].Advances in Adaptive Data Analysis，2009，1(1):1－41.

[10]许丽利.聚类分析的算法及应用[D].长春:吉林大学，2010.

[11]Ho D，Randall R B.Optimization of bearing diagnostic techniques using simulated and actual bearing fault signals[J].Mechanical Systems and Signal Processing，2000，14(5):763 －788.

[12]Bearing Data Center Website，Case Western Reserve University，http://www.eecs.cwru.edu/laboratory/bearing.