皮羌走滑断裂控制构造裂缝发育的力学机制模拟
2012-09-13张庆莲侯贵廷潘文庆韩剑发李乐鞠玮
张庆莲,侯贵廷,潘文庆,韩剑发,李乐,鞠玮
(1.造山带与地壳演化教育部重点实验室/北京大学地球与空间科学学院,北京100871; 2.北京大学石油与天然气研究中心,北京100871; 3.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒841000)
皮羌走滑断裂控制构造裂缝发育的力学机制模拟
张庆莲1,2,侯贵廷1,2,潘文庆3,韩剑发3,李乐1,2,鞠玮1,2
(1.造山带与地壳演化教育部重点实验室/北京大学地球与空间科学学院,北京100871; 2.北京大学石油与天然气研究中心,北京100871; 3.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒841000)
在深入探讨皮羌走滑断裂对构造裂缝控制作用的基础上,应用ANSYS有限元方法,模拟区域差应力、走滑断裂宽度和走向等因素影响下构造裂缝分布发育的规律。模拟结果表明,构造裂缝带宽随区域差应力增大呈线性增大,随断裂带宽度增大呈线性减小,随断裂走向与区域差应力夹角增大呈线性减小;施加的区域差应力值是影响构造裂缝发育的主要因素。
皮羌走滑断裂;构造裂缝;数值模拟;构造应力场;有限元
0 引言
根据弹性力学及断裂力学相关理论,岩石在应力作用下变形能够积聚应变能[1],当岩石内应变能释放率等于产生单位面积裂缝表面所需能量(表面能密度)时即发生断裂[1~5]。由走滑断层而产生的构造裂缝称为走滑断层相关裂缝,相应的裂缝带称为走滑断层控制裂缝带。
动力学研究是构造变形及其形成机制研究的重要方面[6~9],其主要内容是探索构造形变与应力状态之间的关系,以便研究构造的形成机制[7,10~18]。构造裂缝的发育规律、形态和空间分布特征以及渗流规律主要受控于构造应力场和岩石物理性质[9,19~21]。从构造力学和应力场的角度出发,研究构造裂缝形成的力学机制,对构造裂缝预测具有重要意义[22~23]。目前构造应力场的定量研究已经有了比较成熟的方法,其中有限元数值模拟方法应用最为广泛,因此国内外学者多采用构造应力场数值模拟的方法预测构造裂缝[24~26]。
Bertoluzza等采用有限元方法从理论上分析了不同拉分盆地内的应力场分布,并据此分析了石炭-二叠纪南阿尔卑斯地区Collio和Pramollo拉分盆地的动力学形成机制[27];王红罡通过建立反演模型,用有限元方法反演了潜山区的构造应力场分布[28];Homberg等借助数值模拟方法恢复了晚白垩纪法国Pontarlier断裂区的古构造应力场,并通过对主断裂周围应力状态的分析得出了其构造活动规律[29];Hou等以古岩墙为证据,利用有限元数值模拟方法恢复了华北克拉通前寒武纪古构造应力场,为超大陆古构造应力场的重建及超大陆裂解机制的研究提供了参考[30];佟彦明利用ANSYS系统的平面线弹性模拟加以验证,确定了胶莱盆地在莱阳期的动力学机制[31];孙宏斌等利用构造裂隙发育的有限元法模拟技术提出了葵花岛构造在模拟应力场情况下,裂隙发育最有利的地区[32]。这些研究表明,利用数值模拟方法研究构造应力场十分有效。
本文尝试以新疆巴楚皮羌走滑断裂控制构造裂缝发育的地质模型为基础,利用有限元数值模拟的方法,对走滑断层控制构造裂缝发育的多种因素分别进行数值模拟和回归分析,定量地分析各种因素对走滑断层控制裂缝发育的影响。
1 研究区地质背景
研究区位于塔里木盆地的西北缘,主要构造为北东东向的柯坪构造带和北西向的巴楚隆起,两者之间的边界为柯坪塔格山前冲断带(见图1)。新近纪以来由于印度板块与欧亚板块碰撞的远距离效应和西南天山地区板内造山的影响,在上新世末—更新世初柯坪构造带沿柯坪塔格—沙井子断裂带发生强烈挤压,形成5排柯坪塔格逆冲推覆构造带[32~34]。本文以皮羌断裂控制裂缝发育的地质模型为基础,通过有限元数值模拟方法研究走滑断裂控制裂缝发育的主要因素。
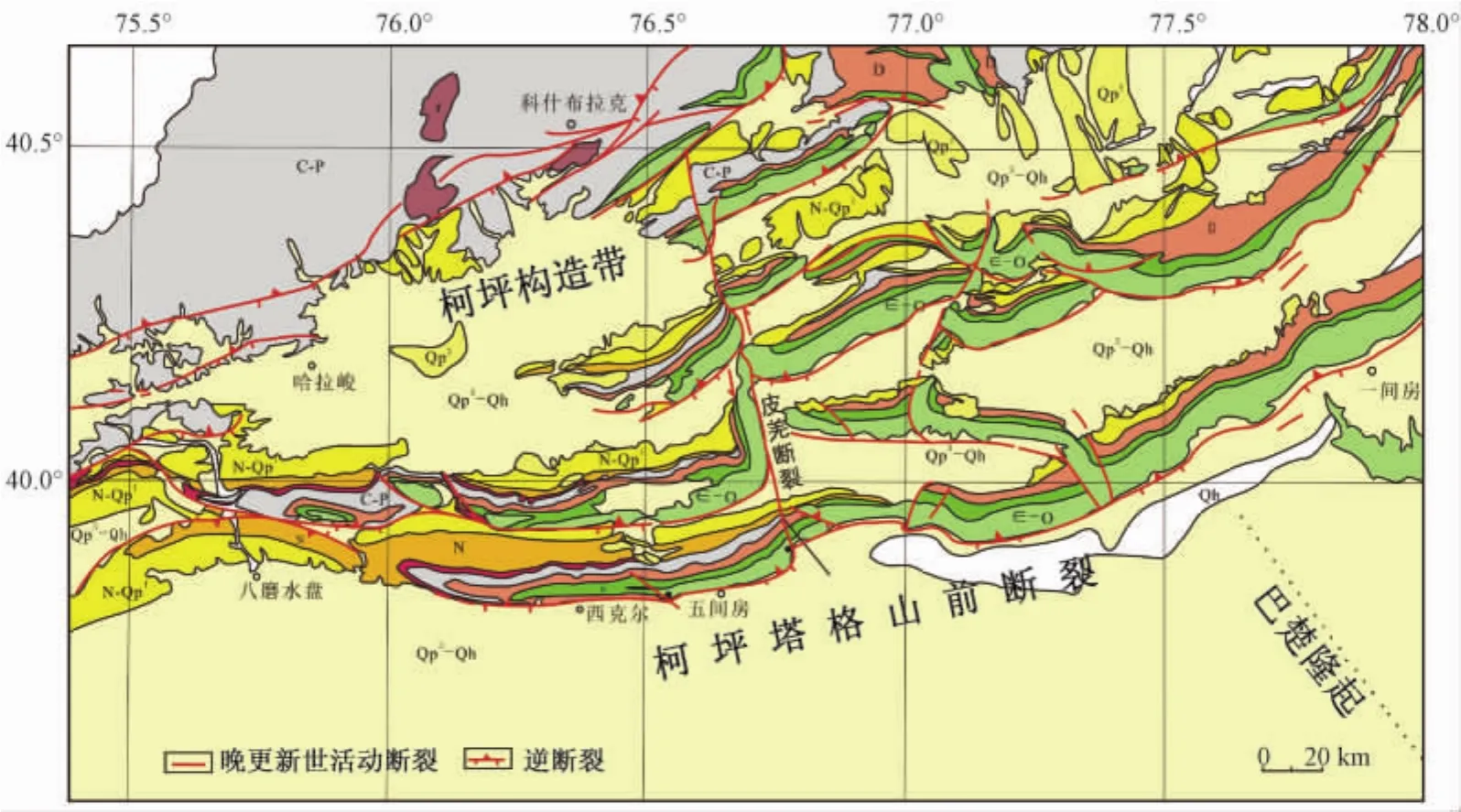
图1 巴楚区域地质及皮羌断裂位置图Fig.1 The regional geological map of Bachu and local map of Piqiang strike-slip fault
皮羌走滑断裂的走向为340°,宽度50 m,长度70 km,水平滑距4 km,为一条错开柯坪塔格构造带的左旋走滑断裂。垂直走滑断层走向布置了9个测点,通过野外数据计算得出每个测点的裂缝面密度,再通过对裂缝面密度和各测点距断裂的距离之间的比较,研究得出了皮羌走滑断裂控制构造裂缝分布发育的规律(见图2),即随距断裂距离的增大,构造裂缝面密度呈指数减小[35]。

图2 皮羌断裂控制构造裂缝分布发育规律Fig.2 The distance-surface density fitting chart of Piqiang strike-slip fault
但上述的皮羌走滑断裂控制裂缝发育的地质模型局限于野外的实际测量,受到野外露头或现实因素的影响,如无法考虑到施加应力改变或断裂走向与应力夹角改变对构造裂缝分布发育的影响,因此,不能更加全面地分析影响构造裂缝分布发育的各种因素。
考虑到这些局限性,本文应用有限元数值模拟方法,将野外有限的由实际构造裂缝测量建立起来的地质模型进行扩展,从更广泛的角度去考虑影响构造裂缝分布发育的各种因素,从而找出控制构造裂缝发育的最重要因素。
2 研究方法及模型的建立
本文主要通过有限元数值模拟方法研究走滑断裂的各种因素对构造裂缝的控制作用。首先通过研究区已有的地质研究成果建立地质构造格架,即建立地质模型;再对地质模型进行简化,建立几何模型;通过岩石力学试验确定模拟所需的各种岩石力学参数;通过确立边界应力方向,设定力学边界条件;然后根据几何模型、岩石力学参数赋值和边界条件建立力学模型。力学模型确立后,将该模型输入到ANSYS 10.0弹性有限元软件进行计算,最终输出构造应力场图[36~38]。在计算过程中,改变影响构造裂缝发育的各种因素(施加的区域差应力值、走滑断裂的走向和宽度等),随着各种因素的改变,统计走滑断裂控制的构造裂缝带宽度的变化,从而定量分析各种因素对走滑断层控制裂缝发育的影响程度。
2.1 建立地质模型
皮羌走滑断裂是在西南天山向南南东挤压的构造应力作用下形成的,形成时间为新近纪上新世—第四纪,它控制了中更新统沉积物的分布。本文选择皮羌断裂及断裂附近的奥陶系灰岩发育区作为研究区,将该区视为连续介质体,并将研究的区域划分为具有不同岩石力学性质的断裂带区和奥陶系灰岩分布区(见图3)。构造裂缝的产生属于岩石的脆性破裂,破裂后具有明显的应力降,因此地质体按线弹性处理,用薄板模型的线弹性理论计算。
2.2 建立几何模型
本次模拟采用二维平面模拟,将地质模型简化为具有一定厚度的平面薄板模型,不考虑垂向应力。采用8节点Plane 82单元和Surfer 153表面效应单元对模型进行模拟。由于模型比较简单,不需要局部网格的人工细化操作,所以对模型进行了自动网格剖分。

图3 皮羌走滑断裂及研究区域的地质模型Fig.3 Geological model of Piqiang strike-slip fault and the study area
2.3 建立力学模型
Reynolds等[39]通过大量的野外测量发现,除了个别应力集中区外大陆内部的差应力值的大小一般不超过50 MPa。所以在本次模拟过程中,所取的应力大小在0~50 MPa之间。
通过23个样品的岩石力学测试获得研究区灰岩的岩石力学参数。灰岩的平均密度为2662 kg/m3,平均弹性模量为70 GPa,平均泊松比为0.27,灰岩的平均抗张强度为8.5 MPa。当某区域的应力值超过抗张强度时,说明该区域的张裂缝发育。断层当作断裂带处理,其岩石的风干密度设为1900 kg/m3,弹性模量为15 GPa,泊松比为0.14[40]。将模拟区域适当放大,以减小模拟过程中的边界效应。以下模拟计算过程中将远离断裂带的4个端点(相对稳定、变形较小)设为固定约束,分别在断裂两侧的灰岩区上施加垂直于边界的区域差应力(见图4)。

图4 皮羌走滑断裂及研究区域的平面力学模型Fig.4 Plane mechanical model of Piqiang strike-slip fault and study area
3 走滑断裂对构造裂缝的控制因素
3.1 施加的区域差应力对构造裂缝发育的影响
通过不断改变施加的区域差应力值,统计在不同区域差应力值下,张裂缝发育带宽度,并将施加的区域差应力值与张裂缝发育带宽度进行拟合,定量分析施加的区域差应力值对构造裂缝发育的影响。
在模拟中,固定4个端点的x、y方向位移,施加的区域差应力与断裂走向之间夹角为10°,断裂带宽度设为50 m,垂直两条边界所施加的区域差应力值分别为10 MPa、11 MPa、12 MPa、15 MPa、20 MPa、30 MPa、40 MPa。施加10 MPa差应力时,模型结果如图5a。统一将张裂缝发育最宽处作为统计裂缝带发育带宽度的位置,经计算得出在各个差应力值下张裂缝发育带宽度(见表1)。

图5 改变施加的区域差应力条件下构造裂缝分布发育图Fig.5 The distribution of the tension fractures under the influence of the deviatoric stress
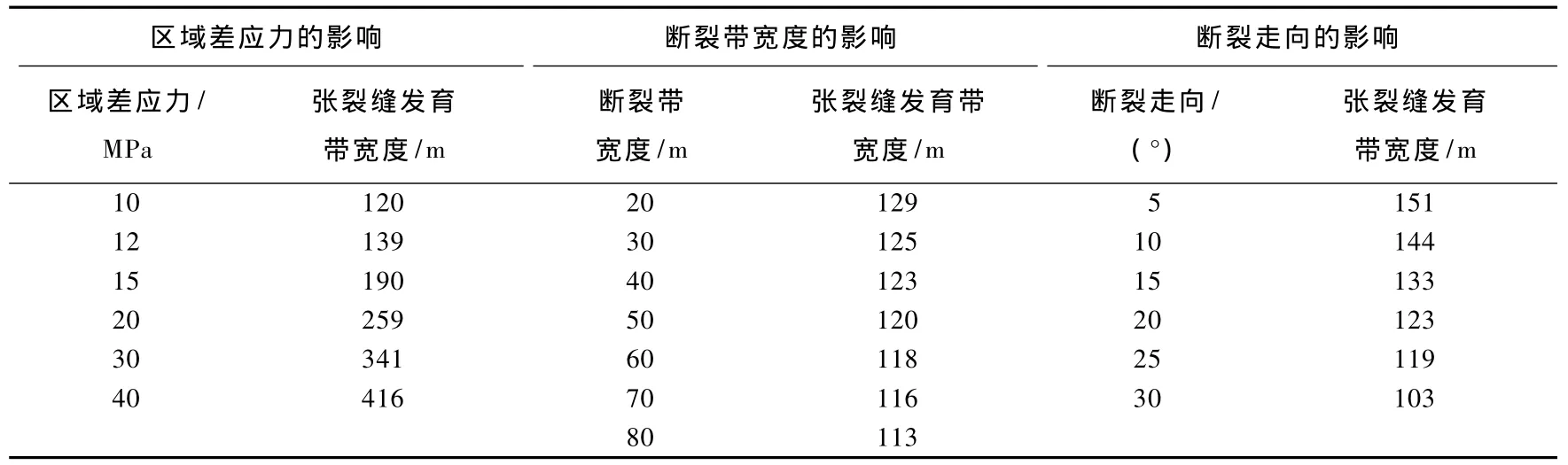
表1 不同影响因素下张裂缝发育带宽度统计Table1 The data of the width of tension fractu re and the influence factor
运用MATLAB软件,对施加的区域差应力值和张裂缝发育带宽度两组数据进行拟合,拟合结果为:施加的区域差应力值与张裂缝发育带宽度呈线性变化,即随着施加的区域差应力逐渐变大,张裂缝发育带宽度呈线性增加(见图5b)。
3.2 断裂带宽度对构造裂缝发育的影响
通过不断改变断裂带宽度,统计在不同断裂带宽度条件下张裂缝发育带宽度,将张裂缝发育带宽度与断裂带的宽度进行拟合,定量分析断裂带宽度对构造裂缝发育程度的影响。建立不同断裂带宽度的走滑断裂模型,固定4个端点x、y向位移,施加的区域差应力和断裂走向之间的夹角为10°,垂直两条边界所施加的区域差应力为10 MPa,断裂带宽度分别为20 m、30 m、40 m、50 m、60 m、70 m、80 m。断裂带宽度为20 m时,模拟结果如图6a。统一将张裂缝发育最宽处作为统计裂缝发育带宽度的位置,经计算得出在各个断裂带宽度下,张裂缝发育带宽度(见表1)。
运用MATLAB软件,对断裂带宽度和张裂缝发育带宽度两组数据进行拟合,拟合结果为:断裂带宽度与张裂缝发育带宽度呈线性负相关关系,即随着断裂带宽度逐渐变大,张裂缝发育带宽度呈线性减小(见图6b)。

图6 改变断裂带宽度条件下构造裂缝分布发育图Fig.6 The distribution of the tension fractures under the influence of the width of the strike-slip fault
3.3 断裂走向对构造裂缝发育的影响
改变走滑断裂的走向即改变走滑断裂与所施加差应力之间的夹角。考虑到施加的区域差应力有垂直于断裂和平行于断裂2个分量,而此处只分析在走滑条件下施加的区域差应力与断裂走向间夹角变化对构造裂缝发育的影响,故建立力学模型时,将断裂设置为滑轮支撑边界,即固定断裂的x向位移,只有y向位移,忽略垂直于断裂的分量对构造裂缝的影响,只考虑在走滑分量作用下构造裂缝的发育情况。
建立不同断裂走向的走滑断裂模型,固定4个端点x、y向位移及断裂x向位移,垂直2条边界所施加的区域差应力为10 MPa,断裂带宽度为50 m,施加的区域差应力和断裂走向之间的夹角分别为5°、10°、15°、20°、25°、30°。夹角为15°时,模拟结果如图7a。统一将张裂缝发育最宽处作为统计裂缝带发育带宽度的位置,经计算得出在各个断裂走向下张裂缝发育带宽度(见表1)。
运用MATLAB软件,对断裂走向和张裂缝发育带宽度两组数据进行拟合,拟合结果为:断裂走向与张裂缝发育带宽度呈线性负相关关系,即随着断裂走向与施加差应力方向夹角的增大,张裂缝发育带宽度呈线性减小(见图7b)。
当断裂走向与施加的差应力之间的夹角变大时,实际上作用于断裂上的走滑分量越来越小,因此由走滑作用引起的构造裂缝(张裂缝)越来越不发育。
3.4 张裂缝发育带宽的影响因素
通过以上应力场数值模拟,得到了在不同地质条件下的张裂缝发育带宽度,对张裂缝发育带宽度与各个影响因素的数据进行拟合,得到了在施加的区域差应力、走滑断裂带宽度和走向3个因素影响下张裂缝的发育趋势,通过对拟合公式中斜率大小的比较可以确定影响张裂缝发育的最重要因素(见表2)。本文认为斜率值最大的因素是走滑断裂控制张裂缝发育的最重要因素。
由表2可以看出,施加的区域差应力这一影响因素的斜率值最大,说明所施加的区域差应力对张裂缝的控制作用最为强烈,也是影响张裂缝发育的最重要因素。
应力与应变呈正比,反映在走滑断裂上即走滑断裂的滑移距离与所受的区域差应力值呈正比,因此可以认为滑移距离是影响走滑断裂周围构造裂缝发育的最重要因素。

图7 改变断裂走向条件下构造裂缝分布发育图Fig.7 The distribution of the tension fractures under the influence of the trend of the strike-slip fault

表2 张裂缝发育各影响因素拟合公式斜率和相关系数Table2 The data of the slope and the correlation coefficient
4 结论
构造裂缝(张裂缝)的发育带宽随施加的区域差应力增大而线性增大,随走滑断裂带宽度增大而线性减小,随走滑断裂走向与区域差应力夹角增大而线性减小。比较三种影响因素拟合公式的斜率后认为,施加的区域差应力值是影响构造裂缝(张裂缝)发育的最重要因素。
应力与应变呈正比,反映在走滑断裂上即走滑断裂的滑移距离与所受的区域差应力值呈正比,因此可以认为滑移距离是影响走滑断裂周围构造裂缝发育的最重要因素,在碳酸盐岩地区研究走滑断裂控制构造裂缝发育规律时要重点考虑走滑位移量。
致谢舒武林和鞠玮参加了野外构造裂缝测量,张鹏和孟庆峰参与了室内数据处理工作,一并感谢。
[1]王仁,丁中一,殷有泉.固体力学基础[M].北京:地质出版社,1979.WANG Ren,DING Zhong-yi,YIN You-qun.Solid mechanics[M].Beijing:Geological Publishing House,1979.
[2]文世鹏,李德同.储层构造裂缝数值模拟技术[J].石油大学学报,1996,20(5):17~24.WEN Shi-peng,LI De-tong.Numerical simulation technology for structural fracture of reservoir[J].Journal of the University of Petroleum,1996,20(5):17~24.
[3]曹春富,孙绍春,张吉昌.利用有限元法定量预测变质岩储层构造裂缝[J].特种油气藏,1997,4(1):24~28.CAO Chun-fu,SUN Shao-chun,ZHANG Ji-chang.Quantitative prediction of structural fractures of metamorphic rock reservoir by finite element[J].Special Oil&Gas Reservoirs,1997,4(1):24~28.
[4]丁中一,钱祥麟,霍红,等.构造裂缝定量预测的一种新方法——二元法[J].石油与天然气地质,1998,19 (1):1~7.DING Zhong-yi,QIAN Xiang-lin,HUO Hong,et al.A new method for quantitative prediction of tectonic fractures:Twofactor method[J].Oil&Gas Geology,1998,19(1):1~7.
[5]陈波,田崇鲁.储层构造裂缝数值模拟技术的应用实例[J].石油学报,1998,19(4):50~54.CHEN Bo,TIAN Chong-lu.Numerical simulation technique for structural fractures in a reservoir:Case studies[J].Acta Petrolei Sinica,1998,19(4):50~54.
[6]宋惠珍.脆性岩储层裂缝定量预测的尝试[J].地质力学学报,1999,5(1):76~84.SONG Hui-zhen.An attempt of quantitative prediction of natural crack on brittle rock reservoir[J].Journal of Geomechanics,1999,5(1):76~84.
[7]谭成轩,王连捷.三维构造应力场数值模拟在含油气盆地构造裂缝分析中应用初探[J].地球学报,1999,20 (4):392~394.TAN Cheng-xuan,WANG Lian-jie.An approach to the application of 3-D tectonic stress field numerical simulation in structural fissure analysis of the oil-gas-bearing basin[J].Acta Geoscientia Sinica,1999,20(4):392~394.
[8]孙焕泉,王加滢.地下构造裂缝分布规律及其预测[J].大庆石油学院学报,2000,24(3):83~85.SUN Huan-quan,WANG Jia-ying.Distribution law of underground structural fissures and their forecasting[J].Journal of Daqing Petroleum Institute,2000,24(3):83~85.
[9]李淑恩,张绍辉,岳奎,等.构造应力场数值模拟分析技术及其应用[J].油气地质与采收率,2001,8(6): 38~40.LI Shu-en,ZHANG Shao-hui,YUE Kui,et al.Numerical simulation analysis technique of structural stress field and its application[J].Petroleum Geology and Recovery Efficiency,2001,8(6):38~40.
[10]陈艳华,朱庆杰,苏幼坡.基于格里菲斯准则的地下岩体天然裂缝分布的有限元模拟研究[J].岩石力学与工程学报,2003,22(3):364~369.CHEN Yan-hua,ZHU Qing-jie,SU You-po.Finite element research on natural fracture distribution in underground rocks according to Griffith criterion[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(3):364~369.
[11]何光明,高如曾.分形理论在裂缝预测中的尝试[J].石油物探,1993,32(2):1~13.HE Guang-ming,GAO Ru-zeng.Fracture prediction based on fractal theory[J].Geophysical Prospecting for Petroleum,1993,32(2):1~13.
[12]侯贵廷.裂缝的分形分析方法[J].应用基础与工程科学学报,1994,2(4):299~305.HOU Gui-ting.Fractal analysis of fractures[J].Journal of Basic Science and Engineering,1994,2(4):299~305.
[13]万天丰.古构造应力场[M].北京:地质出版社,1988:4~10.WAN Tian-feng.Paleotectonic stress field[M].Beijing:Geological Publishing House,1988:4~10.
[14]张明利,万天丰.含油气盆地构造应力场研究新进展[J].地球科学进展,1998,13(1):38~43.ZHANG Ming-li,WAN Tian-feng.The new research development of tectonic stress field in oil and gas basin[J].Advances in Earth Sciences,1998,13(1):38~43.
[15]Martin A M,Cloeginch S,Vicente G D,et al.Finite-element modeling of Tertiary paleostress field in the eastern part of the Tajo Basin(central Spain)[J].Tectonophysics,1998,300(1~4):47~62.
[16]孙宏斌,陈汉林,程晓敢,等.辽河盆地葵花岛构造裂隙发育的有限元模拟[J].地质科学,2004,39(2): 199~205.SUN Hong-bin,CHEN Han-lin,CHENG Xiao-gan,et al.Finite element simulation of fracture development in the Kuihuadao Structure,Liaohe Basin[J].Chinese Journal of Geology,2004,39(2):199~205.
[17]童亨茂,郑磊.三维地震资料在古应力场反演和裂缝预测中的应用——以胜利油田富台潜山为例[J].地质科学,2007,42(1):45~57.TONG Heng-mao,ZHENG Lei.Applications of 3D seismic data in paleo-tectonic stress field backward modeling and fissures prediction:A case study from the Futai Buried Hill,Shengli oilfield[J].Chinese Journal of Geology,2007,42(1):45~57.
[18]王连捷,王红才,王薇,等.油田三维构造应力场、裂缝与油气运移[J].岩石力学与工程学报,2004,23 (23):4052~4057.WANG Lian-jie,WANG Hong-cai,WANG Wei,et al.Relation among three dimensional tectonic stress field,fracture and migration of oil and gas in oil field[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(23):4052~4057.
[19]Joussineau G D,Petit J P,Gauthier B D.Photoelastic and numerical investigation of stress distributions around fault models under biaxial compressive loading conditions[J].Tectonophysics,2003,363(1~2):19~43.
[20]Maerten L,Gillespie P,Pollard D D.Effects of local stress perturbation on secondary fault development[J].Journal of Structural Geology,2002,24(1):145~153.
[21]万天丰.中国中、新生代板内变形与构造应力场[J].地质力学学报,1996,2(3):13.WAN Tian-feng.The Mesozoic and Cenozoic intraplate deformation and tectonic stress field in China[J].Journal of Geomechanics,1996,2(3):13.
[22]万天丰,任之鹤.中国中、新生代板内变形速度研究[J].现代地质,1999,13(1):83~92.WAN Tian-feng,REN Zhi-he.Research on the intraplate deformation velocity of China in Meso Cenozoic[J].Geoscience,1999,13(1):83~92.
[23]童亨茂.储层裂缝描述与预测研究进展[J].新疆石油学院学报,2004,16(2):9~13.TONG Heng-mao.Description and prediction of reservoir fractures networks[J].Journal of Xinjiang Petroleum Institute,2004,16(2):9~13.
[24]操成杰.川西北地区构造应力场分析与应用[D].西安:西北大学,2001.CAO Cheng-jie.Analysis and application of tectonic stress field in the northwestern Sichuan Basin[D].Xi’an: Northwestern University,2001
[25]张乐,姜在兴,郭振廷.构造应力与油气成藏关系[J].天然气地球科学,2007,18(1):31~35.ZHANG Le,JIANG Zai-xing,GUO Zhen-ting.Relationship between structural stress and hydrocarbon bearing pool formation[J].Natural Gas Geoscience,2007,18(1):31~35.
[26]刘佑荣,唐辉明.岩体力学[M].武汉:中国地质大学出版社,2008.LIU You-rong,TANG Hui-ming.Rockmass mechanics[M].Wuhan:China University of Geosciences Press,2008.
[27]Bertoluzza L,Perotti C R.A finite-element model of the stress field in strike-slip basins:Implication for the Permian tectonics of the southern Alps(Italy)[J].Tectonophysics,1997,280(1~2):185~197.
[28]王红罡,吕炳全,徐国强,等.胜利油田埕北30潜山裂缝系统的地应力有限元法分析[J].上海地质,2003,(2):26~30.WANG Hong-gang,LÜ Bing-quan,XU Guo-qiang,et al.Finite element analysis on paleotectonic stress of buried hill seaming system in Chenbei 30 of Shengli Oilfield[J].Shanghai Geology,2003,(2):26~30
[29]Homberg C,Angelier J,Bergerat F.et al.Using stress deflections to identify slip events in fault systems[J].Earth and Planetary Science Letters,2004,217(3~4):409~424.
[30]Hou G T,Wang C C,Li J H,et al.Late paleoproterozoic extension and a paleostress field reconstruction of the North China Craton[J].Tectonophysics,2006,422(1~4):89~98.
[31]佟彦明.胶莱盆地莱阳期古构造应力场分析及模拟[J].大庆石油地质与开发,2007,26(1):6~9.TONG Yan-ming.The paletectonic stress field at Laiyang Stage in Jiaolai Basin and the simulation[J].Petroleum Geology&Oilfield Development in Daqing,2007,26(1):6~9.
[32]宋方敏,闵伟,韩竹军,等.南天山柯坪塔格推覆体前缘断裂活动性质及速率[J].地震地质,2007,29(2): 272~281.SONG Fang-min,MEN Wei,HAN Zhu-jun,et al.Activities and slip rate of the frontal faults of the Kalpingtag nappe,Tianshan Mountains,China[J].Seismology and Geology,2007,29(2):272~281.
[33]曲国胜,李亦纲,陈杰,等.柯坪塔格推覆构造几何学、运动学及其构造演化[J].地学前缘,2003,10(增刊):142~150.QU Guo-sheng,LI Yi-gang,CHEN Jie,et al.Geometry,kinematics and tectonic evolution of Kepingtage thrust system[J].Earth Science Frontiers,2003,10(Supp.):142~150.
[34]杨晓平,冉勇康,宋方敏,等.西南天山柯坪逆冲推覆构造带的地壳缩短分析[J].地震地质,2006,28(2): 194~203.YANG Xiao-ping,RAN Yong-kang,SONG Fang-min,et al.The analysis for crust shortening of Kalpin thrust tectonic zone,southwestern Tianshan,Xinjiang,China[J].Seismology and Geology,2006,28(2):194~203.
[35]张庆莲,侯贵廷,潘文庆,等.新疆巴楚地区走滑断裂对碳酸盐岩构造裂缝发育的控制[J].地质通报,2010,29(8):1160~1167.ZHANG Qing-lian,HOU Gui-ting,PAN Wen-qing,et al.Development of fractures in carbonate rocks under the influence of strike-slip faults in Bachu area,Xinjiang,China[J].Geological Bulletin of China,2010,29(8):1160~1167.
[36]莫维尼.有限元分析:ANSYS理论与应用[M].欧阳宇译.北京:电子工业出版社,2003.Moaven I S.Finite element analysis:Theory and application of ANSYS[M].OUYANG Yu(Translated).Beijing: Publishing House of Electronics Industry,2003.
[37]刘涛,杨凤鹏.精通ANSYS[M].北京:清华大学出版社,2002.LIU Tao,YANG Feng-peng.Proficient in ANSYS[M].Being:Tsinghua University Press,2002.
[38]蒋有录,张乐,鲁雪松,等.基于ANSYS的应力场模拟在库车坳陷克拉苏地区的初步应用[J].天然气工业,2005,25(4):42~44.JIANG You-lu,ZHANG Le,LU Xue-song,et al.Application of the tectonic stress field simulation based on ANSYS in Kelasu region of Kuche depression[J].Natural Gas Industry,2005,25(4):42~44.
[39]Reynolds S D,Coblentz D D,Hillis R R.Tectonic forces controlling the regional interpolate stress field in continental Australia:Results from new finite element modeling[J].Geophys.Res.,2002,107(B7):2131
[40]王岩欣,侯贵廷,李江海,等.塔北隆起中西部新近纪末构造应力场数值模拟[J].北京大学学报,2008,3 (30):52~57.WANG Yan-xin,HOU Gui-ting,LI Jiang-hai,et al.Numercial simulation of tectonic stress field at the end of Neocene in the Midwest of Tabei uplift[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2008,3(30):52~57.
Abstract:Based on the intensive research on development of structural fractures that controlled by the Piqiang strike-slip fault,this paper has simulated the distribution of structural fractures under the influence of the regional deviatoric stress,the width and trend of the strike-slip fault through the“ANSYS”finite element method.The simulating results indicated that the width of the fractures increased linearly with the increase of the regional deviatoric stress,decreased linearly with the increase of the width of the faulted belt,and decreased linearly with the increase of the angle between regional deviatoric stress and the fault trend.The regional deviatoric stress is the main factor that controls the development of the fractures.
Key words:Piqiang strike-slip fault;structural fracture;numerical simulation;tectonic stress field;finite element
NUMERICAL SIMULATION OF STRUCTURAL FRACTURES CONTROLLED BY PIQIANG STRIKE-SLIP FAULT
ZHANG Qing-lian1,2,HOU Gui-ting1,2,PAN Wen-qing3,HAN Jian-fa3,LI Le1,2,JU Wei1,2
(1.School of Earth and Space Science,Peking University/Key Laboratory of Orogenic Belts and Crustal Evolution,Ministry of Education,Beijing100871,China; 2.Institute of Oil and Gas Research,Peking University,Beijing100871,China; 3.Institute of Exploration and Development,PetroChina Tarim Oil and Gas Branch Company,Korla841000,China)
P554
A
1006-6616(2012)02-0110-10
2012-01-04
国家重点基础研究发展计划“973”项目(2009CB219302)
张庆莲(1986-),女,北京大学地球与空间科学学院博士研究生,主要从事石油地质研究。E-mail: zhangqinglian@pku.edu.cn
侯贵廷(1964-),男,教授,博士生导师,主要从事石油地质研究。E-mail:gthou@pku.edu.cn
