基于小世界网络的 PSO算法在电力系统中的应用❋

唐京瑞,毕贵红,王 曦

(昆明理工大学 电力工程学院,云南 昆明 650051)

电力系统中发电机组的优化组合是指在一个调度周期(24 h)内,在满足系统负荷需求和机组运行安全、备用约束等条件下,合理安排机组的开停机时间以及负荷分配,使此周期内的总运行费

用最小[1].合理优化的机组组合方案能节省大量的燃料费用,延长机组的使用寿命,带来巨大的经济效益,是电力系统经济运行中的一个重要组成部分.由于在实际的电力系统中,机组组合问题受许多约束条件限制,从而使该问题成为复杂的多约束、高维数、非凸非线性规划问题.在处理此类问题时,智能算法显示出了极大的优越性.解决此问题的传统算法有优先顺序法,动态规划法,拉格朗日松弛法,遗传算法,人工神经网络算法以及粒子群算法等,但这些算法存在着收敛速度慢,产生不可行解和易陷入局部最优等缺点[2-3].

粒子群算法 (Particle Swarm Optimization,PSO)是最早由 Kennedy和 Eberhart在 1995年提出的一种基于群体智能的全局随机搜索算法.后来许多国内外学者将此算法作了进一步的深入研究,提出了许多改进的措施,在一定程度上大大提高了算法的优化性能和收敛能力,并将其应用到了各个领域,取得了显著的成效[4-7].算法中每个个体称为一个“粒子”,每个粒子代表着问题的一个潜在解,用位置、速度和适应度值三项指标表示该粒子的特征,通过粒子在空间中的位置和速度的更新等操作,从而使适应度值得到不断的优化提高.PSO算法由于具有很好的生物社会背景而易理解,参数少而易实现,可以考虑多种约束,对复杂的非线性高维参数问题具有较强的全局搜索能力,在科学研究和工程实践中得到了广泛的应用[8].

本文在研究基本粒子群算法的基础上,提出了将小世界网络引入到粒子群算法邻域中,每个粒子通过其邻域粒子间的相互协作与信息共享,可以提高算法的收敛速度和精度,算例仿真表明该算法是有效的.

1 数学模型[9]

为了建立发电机组优化组合的数学模型,首先要对发电机组的各种约束条件进行分析与讨论.

1.1 等式约束

等式约束为机组功率平衡约束.设系统中机组或等值机组数为 G,调度周期为 T,各时段系统总负荷为 PDt,其约束条件如下：

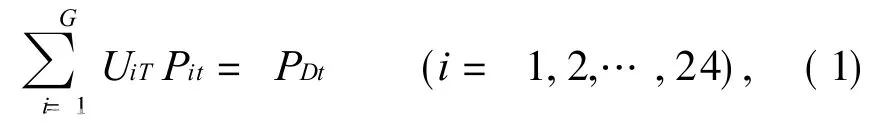
式中：Pit是由 t时段投入运行的发电机组按等耗量微增率进行计算,即满足

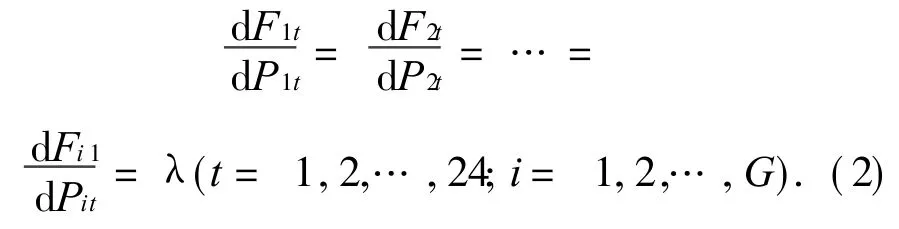
1.2 不等式约束

不等式约束包括旋转备用约束、输出功率约束和开停机时间约束等.在非线性优化问题中,通过罚函数的方法来处理不等式约束,当机组不满足这些约束条件时,就直接将这一个体对应的适应度值置为零.

1.3 目标函数

机组优化组合问题就是在一个调度周期(24 h)内,根据负荷预测满足机组安全以及各种约束条件下,合理安排出参加运行的机组数及机组开停的时间.本文以发电机组在一个调度周期内的总耗量最小为优化目标,设研究周期为 T0=24 h,并将其分成 24个时间段,因此发电机组优化组合的目标函数表示如下：

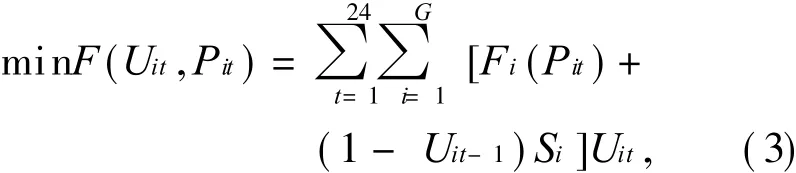
式中：Uit是机组 i在 t时段的运行状态,用 0和 1两个值表示,0表示机组停机,1表示机组开机;Pit是机组 i在时段 t内的输出功率;Fi(Pit)表示发电机组 i在时段 t内的运行耗量,Fi(Pit)=,pi为运行耗量的特性参数);Si是机组 i的启动耗量,它与机组的停机时间 T的长短有关,Si= S0i+ S1i(1-e-T/Ui)(S0i,S1i,Ui为启动耗量特性参数).

2 小世界网络粒子群算法及实现

2.1 基本粒子群算法

粒子群算法 (PSO)是建立在鸟类群体行为研究的基础上,将鸟群中的每一只鸟看作空间中的没有质量和体积的“粒子”,通过这些粒子间的相互协作与信息共享,使其跟踪个体极值 Pbest和群体极值 Gbest来更新个体位置.个体极值 Pbest是指粒子迄今为止搜索到的最佳位置,群体极值Gbest是指整个粒子群迄今为止搜索到的最佳位置.粒子每更新一次位置,就计算一次适应度值[10-11].设在一个 D维空间的搜索空间里,Zi=(Zi1,Zi2,… ,ZiD)为第i个粒子位置矢量,根据目标函数计算出每一个粒子位置相对应的适应度值,即可衡量粒子位置的优劣;第i个粒子的飞行速度 vi=(vi 1,vi 2,…,viD),其个体极值为 Pi=(Pi1,Pi 2,…,Pid),种群的全局极值为 Pg=(Pg1,Pg2,…,PgD).

在每一次迭代中,粒子根据以下式子更新速度和位置：

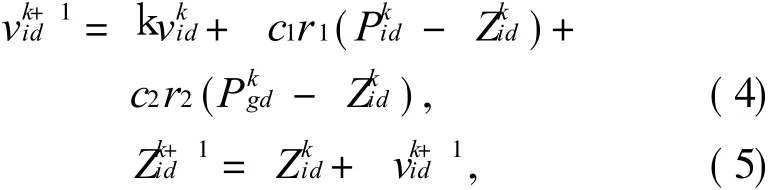
式中：k为惯性权重;k是迭代次数,i=1,2,…,m;d=1,2,… ,D;r1和 r2是 [0,1]之间的随机数;c1和 c2是非负的常数,这两个参数称为加速度因子(亦称学习因子),用来保持种群的多样性[12].

2.2 小世界网络粒子群算法

2.2.1 编码设计

本文的数学模型描述了在时间 t时刻下,N台机组的空间最优状态组合及其对应的最优负荷分配情况,采用小世界网络粒子群算法进行实数矩阵编码,把 N台机组转化成粒子的 N维空间,则机组在 T时间里的有功出力就相应地转化成了粒子在 N维空间上位置的确定.因此,由发电机组的出力 Pit构成的粒子向量表示如下：

式中：Gk是粒子向量,表示粒子群中的第k个个体;Pi,t表示粒子 i的空间位置,含义为发电机组i在 t时刻的发电量大小.

发电机组的运行状态与编码矩阵中的元素取值有关,即根据机组在某一时间段内的有功出力的大小来确定其启停状态,具体表达式为

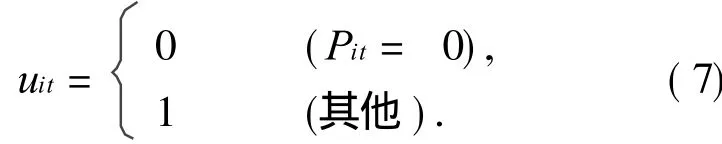
为了使网络模型体现出小世界效应所具有的特性,粒子群的数量必须达到一定的规模.设粒子个数 N=1000,将粒子顺序编号,首尾连接成环,并初始化粒子之间的关系为小世界邻域模型,取节点度 k=4.对每一个粒子进行输出功率计算,通过功率计算可以获得每一个粒子相对应的状态变量及机组出力情况,并与其经历过的最好位置 Pi,t与所在邻域的当前最好位置 Pg,t进行比较、更新和调整,对功率计算获得的机组出力越限情况采用取极限值的方法处理,并根据式(4)和(5)更新粒子的位置和速度,最后当达到最大迭代次数后,输出相关信息.

2.2.2 惯性权重的选择

惯性权重k是影响 PSO算法收敛性的重要参数[13],用来体现粒子当前速度多大程度上继承历史速度.一个较大的惯性权值有利于全局搜索,而一个小的惯性权值更适于局部搜索.因此,为了让粒子去不断地探索新的区域,选择合适的 k值能够平衡 PSO算法的全局和局部搜索能力.实验研究表明：将 k值设为一个随时间线性减小的函数,比将k值设为定值更有利于算法搜索到全局最优解,其惯性权重的函数形式可表示为

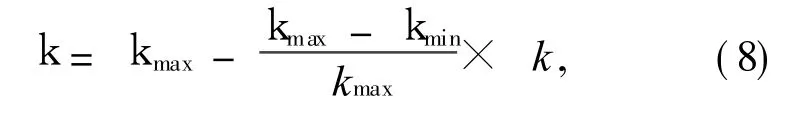
式中：kmax为初始权重;kmin为最终权重;kmax为最大迭代次数;k为当前迭代次数.

2.2.3 小世界邻域模型的构造方法

小世界效应是由 Stanley Milgram通过连锁信实验发现了社会体系中的“六度分割”现象[14],即一个指定节点只需通过极少步骤就能到达另一节点.它揭示了客观世界许多复杂网络中最为有效的信息传递方式.PSO的邻域是指单个粒子与其它粒子之间连接的方式.邻域结构决定了信息在粒子之间传递的强度,它也直接影响着算法的收敛程度.如果信息在粒子之间传递强度过弱,那么会因为单个粒子很难迅速得到离它较远的粒子信息,使得算法收敛速度减慢,影响计算效率;相反,如果信息在粒子之间传递过强,那么很容易使算法陷于早熟.因此,选择合适邻域的粒子群算法,对于寻找全局最优解起着关键性的作用.本文将“平均最短路径小,聚集系数大”的小世界网络模型引入到粒子群算法的邻域结构中,不仅有利于粒子间的信息共享,而且可以提高算法的收敛速度.

小世界网络介于规则网络与随机网络之间,其模型构造方法如下[15]：

1)将每个粒子按照其初始生成顺序编号(1,2,… ,N),然后粒子 i与编号为的k个粒子进行直接相连,最后将编号最大的与编号最小的粒子首尾相连,形成环形规则网络.

2)保持环形规则网络中原来的边不动,对应每个节点 i的每条边,随机选择一个节点 j(i≠j,j-k＞(k/2))以较小的概率 P与节点 i进行长距离连接.构造过程如图 1所示,在形成该模型的过程中不会出现孤立的簇.

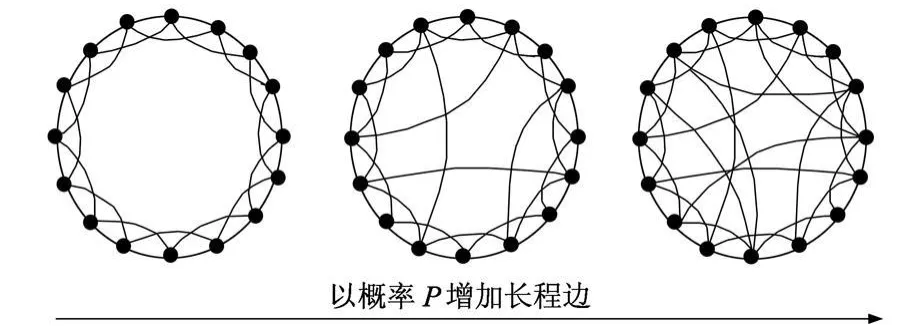
图1 小世界网络邻域的构造过程Fig.1 Construction process of neighborhood of small world network

2.2.4 算法实现

在利用小世界网络邻域结构的 PSO算法求解机组优化组合问题时,为了防止产生孤立群集或者误删关键连接,需要利用公式(4)和(5)不断地对粒子的搜索位置和速度进行调整,即实现粒子的搜索与更新.

实现算法的具体步骤如下：

1)为机组参数赋初值;

2)在满足各种约束的条件下初始化粒子速度和位置;

3)将粒子顺序编号,首尾连接成环,并初始化粒子之间的连接关系为小世界网络模型;

4)计算每个粒子的适应度值,更新粒子的个体极值 Pbest和群体极值 Gbest;

5)按照式(4)和(5)对粒子的位置和速度进行调整.

6)处理与约束条件相冲突的粒子,并将其重新初始化;

7)收敛判断,若未获得一个足够好的适应度值或者未到达最大迭代数,则返回步骤 4),否则输出相关信息.

3 算例分析

按照上述方法,本文利用 Matlab编制了电力系统机组优化组合的小世界网络粒子群算法程序,实验种群规模 N=1000,迭代次数 T=100,学习因子 c1=c2=1,以文献 [16]中介绍的 10机系统进行了计算[16],各机组的运行参数,系统负荷(含网损)和备用容量数据见表 1和表 2,利用 SWNPSO方法计算出有关机组优化组合结果和各时段耗量,见表 3和表 4,其总耗量为 78701.5.同时,还与拉格朗日松弛法,系统进化算法和改进遗传算法进行了比较,比较结果见表 5.

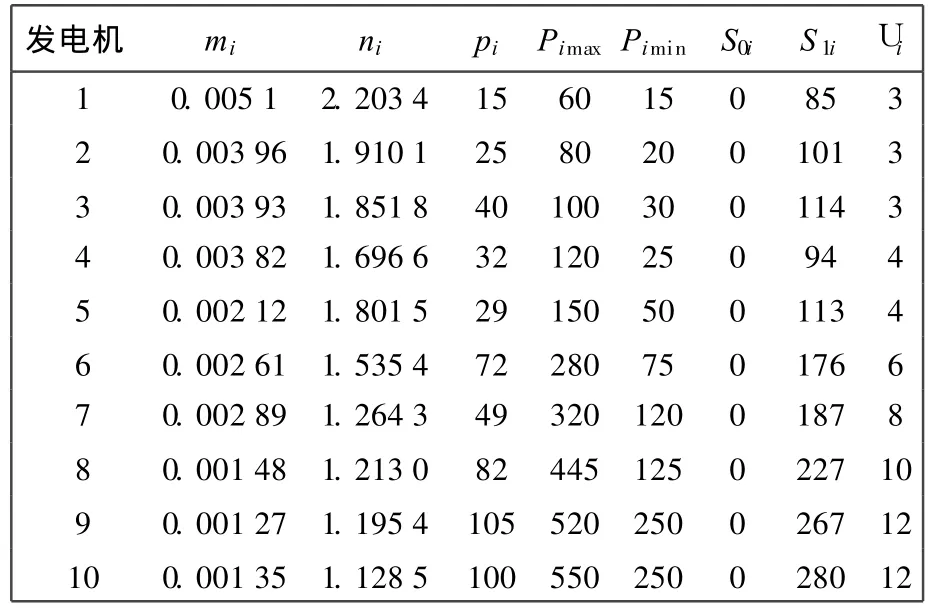
表1 机组特性数据Tab.1 Unit character data

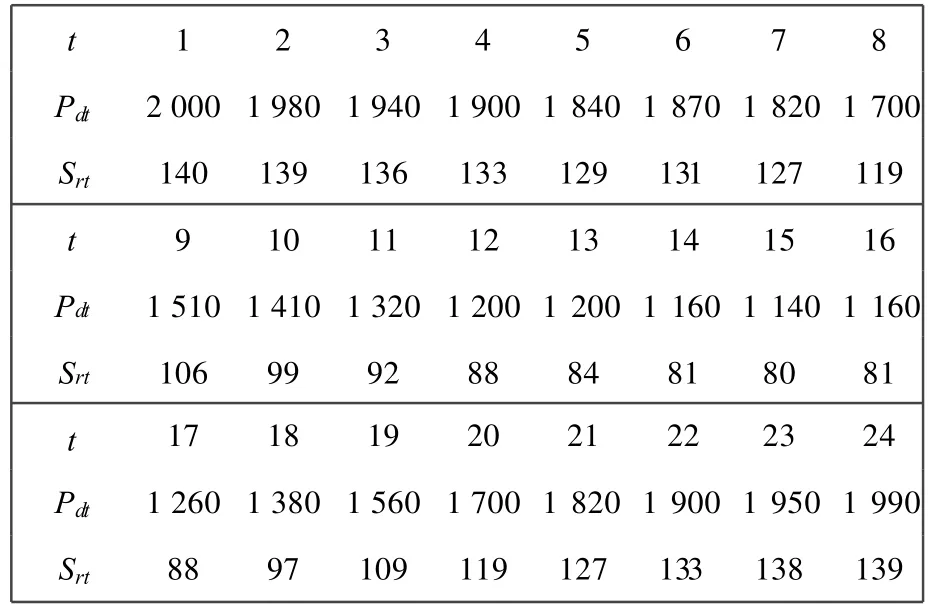
表2 负荷和备用数据Tab.2 Load and reserve data

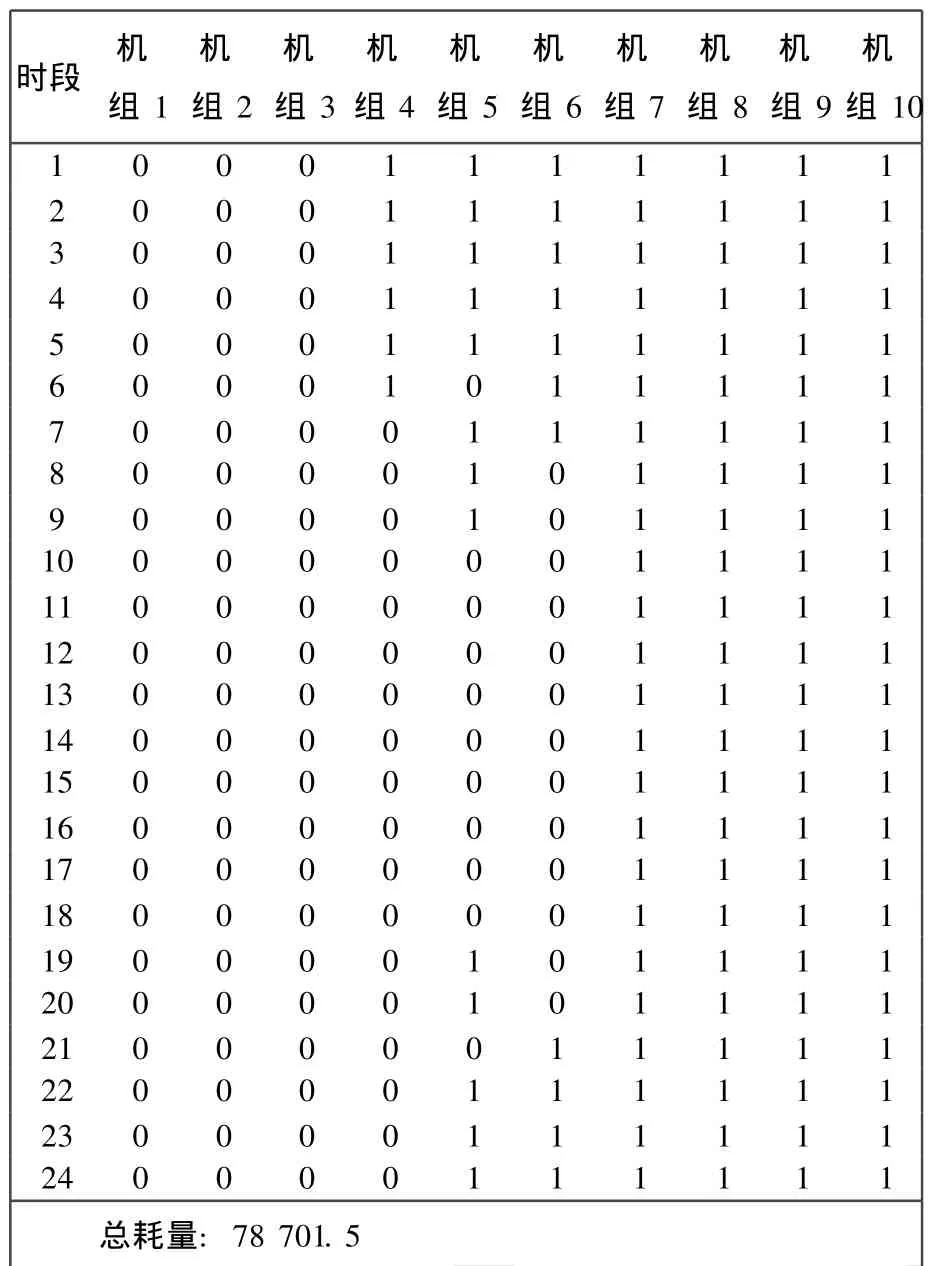
表3 机组优化组合结果Tab.3 Optimal results of unit commitment

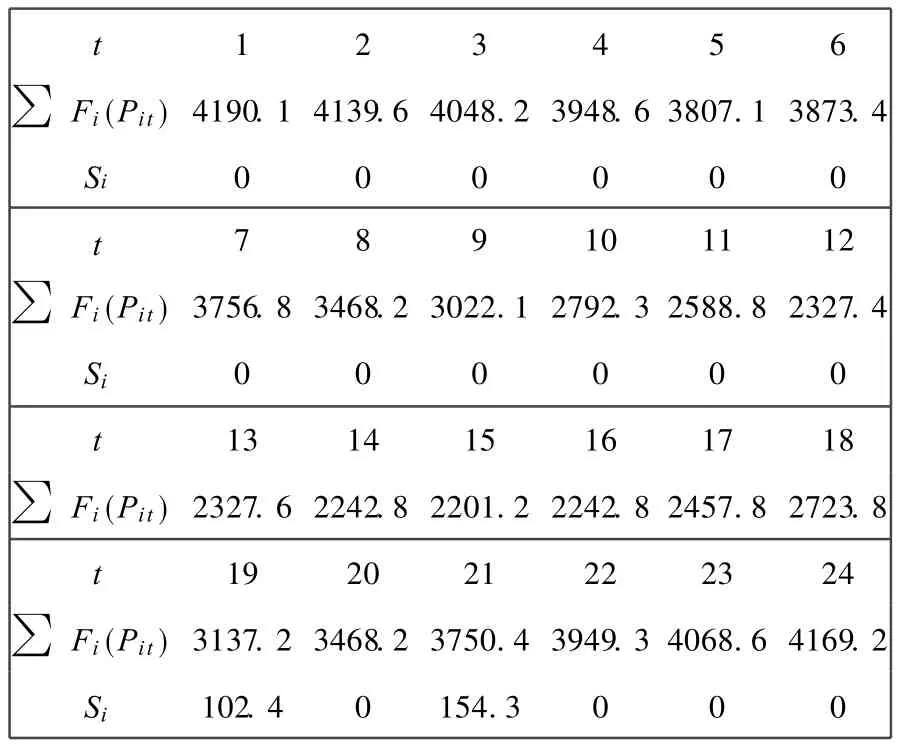
表4 各时段耗量Tab.4 Consumption of each time interval

表5 各优化方法的结果比较Tab.5 The comparison of results using different methods

结合实验数据可以看出,将小世界网络模型邻域结构引入到粒子群算法中,具有粒子间的信息共享,加快收敛速度等优点,改进的 PSO算法比其它几种算法具有更强的全局搜索能力,在满足各种约束条件下,最终结果由改进 PSO算法得到的总耗量最小,获得了更好的经济效益.

4 结 论

本文在考虑机组功率平衡约束,旋转备用约束以及发电机组输出功率上下限等约束条件下,建立了电力系统机组优化组合的数学模型.并将“平均最短路径小,聚集系数大”的小世界网络模型引入到粒子群算法邻域结构中,在 10机系统里进行了仿真计算,结果表明：改进的 PSO算法具有更优的寻优能力,在满足各种相同约束的条件下,获得了更好的经济效益.

[1]Wang S J.Short-term generation scheduling with transmission and environmental constraints using an augmented lagrangian relaxation[J].IEEE Trans on Power Systems,1995,10(3)：1294-1301.

[2]国博.改进粒子群算法在高维复杂函数寻优中的应用[J].计算机工程与应用,2010,46(16)：232-234.Guo Bo. Improved particle swarm optimization algorithm for high-dimension complex functions[J].ComputerEngineering and Applications,2010,46(16)：232-234.(in Chinese)

[3]张洋,罗可.基于改进粒子群算法的聚类算法 [J].计算机工程与应用 ,2009,45(33)：132-134.Zhang Yang,Luo Ke.Clustering method based on improved particle swarm optimization[J].Computer Engineering and Applications,2009,45(33)：132-134.(in Chinese)

[4]陈皓勇,王锡凡.机组组合问题的优化方法综述[J].电力系统自动化,1999,23(4)：51-54.Chen Haoyong,Wang Xifan.A survey of optimization based metheods for unit commitment[J].Automation of Electric Power Systems,1999,23(4)：51-54.(in Chinese)

[5]蔡超豪,蔡元宇.机组优化组合的遗传算法 [J].电网技术 ,1997,21(1)：44-46.CaiChaohao, CaiYuanyu.Optimization ofunit commitment by genetic algorithm[J].Power System Technology,1997,21(1)：44-46.(in Chinese)

[6]夏小翔.基于元胞机的小生境微粒群算法[J].计算机工程与应用,2007,43(11)：66.Xia Xiaoxiang.Niche PSO algorithm based on CA[J].Computer Engineering and Applications,2007,43(11)：66.(in Chinese)

[7]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京：科学出版社,2009：16-18.

[8]Kennedy J,Eberhart R.Particle swarms optimization[C]. Proc IEEE Int Conf on Neural Net Works.Perth,1995：1942-1948.

[9]文劲宇.遗传算法及其在电力系统中的应用(上、下)[J].电力系统自动化,1996(10)：57.Wen Jinyu.Genetic algorithm and its applications to power systems[J]. Automation of Electric Power Systems,1996(10)：57.(in Chinese)

[10]Liang J J,Suganthan P N.Dynamic multi-swarm particle swarm optimizer[C].Proceedings of the IEEE International Swarm Intelligence Symposium,2005：124-128.

[11]Cao P B,Xiao R B.Assembly planning using a novelimmuneapproach[J]. InternationalJournalof Advanced Manufacturing Technology,2007,31(7)：770-779.

[12]Eberhart R,Shi Y.Particle swarm optimization[C].Piscataway： Applications and Resources, Proceedings of IEEE Congress on Evolutionary Computation,2001：81-87.

[13]蒲维,滕欢.改进 PSO算法解决电力系统机组优化组合问题 [J].四川电力技术,2007,30(3)：16-17.Pu Wei,Teng Huan.Improved PSO mgofithm for unit commitment optimization of power system[J].Sichuan Electric Power Technology,2007,30(3)：16-17.(in Chinese)

[14]穆华平.基于动态邻域结构的微粒群算法研究 [D].太原：太原科技大学,2008：7-26.

[15]强金龙,于尔铿.电力系统经济调度 [M].哈尔滨：哈尔滨工业大学出版社,1993：99-103.

[16]Newan M E J,Watts D J.Renormalization group analysis of the small-world network model[J].Physics.Letter.A,1999,263：341-347.

[17]魏萍.基于遗传算法的电力系统日有功优化调度[J].电力系统自动化,1999,23(10)：23-26.WeiPing. Dailygeneration scheduling based on genetic algorithm[J].Automation of Electric Power Systems,1999,23(10)：23-26.(in Chinese)

[18]骆济寿,张川.电力系统优化运行[M].武汉：华中理工大学出版社 ,1990：101-103.

[19]牛奔,李丽,楚湘华.新型多群体协同进化粒子群优化算法 [J].计算机工程与应用,2009,45(3)：28-29.Niu Ben,Li Li,Chu Xianghua.Novel multi-swarm cooperative particle swarm optimization [J].Computer Engineering and Applications,2009,45(3)：28-29.(in Chinese)