高阶QAM载波恢复的FPGA设计实现★
2012-09-12徐步威
徐步威
(电子科技大学电子工程学院, 成都 611731)
0 引言
QAM调制方式特别是高阶QAM调制由于其较高的频谱利用率得到了广泛应用。随着4G技术的研发和数字电视的普及,QAM将更加受到重视。
QAM随着阶数的增加,对载波恢复的要求也越严格。对于高阶QAM载波恢复,一个很重要的问题是盲恢复。它是在没有导频或者训练序列帮助的情况下,根据接收到的QAM信号提取出相位误差信息。但是这种方式中同步带宽和相位抖动情况是一对矛盾问题。针对上述考虑,本文采用双模式切换的极性判决相位检测算法,在捕获模式利用有较大频偏捕获能力的极性判决算法[1],而在跟踪模式中则使用传统的DD算法[2-3],因为DD算法具有很好的跟踪性能。这种算法具有更好的频偏捕获能力和健壮性。
随着微电子技术的发展,FPGA技术也在通信中得到了广泛的应用。其高效的运算与高集成度在通信系统中占据了越来越多的优势。本文阐述的FPGA设计方案也在Altera公司的FPGA芯片上得到了实现。
1 极性判决算法结构及设计
1.1 极性判决算法的结构
极性判决算法锁相环路由判决器,鉴相器,环路滤波器,压控振荡器VCO以及一个乘法器组成。
极性判决算法的结构及信号流程如图1所示。为便于理解,这里简述极性判决算法原理。假设n时刻接收到信号y(n),解调之后得到信号q(n)。然后对信号q(n)进行功率检测,即通过判断q (n )2>τ2(τ为功率检测门限)是否成立来选择需要鉴相的接收信号点。q (n )2<τ2时相位检测输出为0,q (n )2>τ2时相位检测输出该信号点的极性判决值。并将解调后的信号q(n)与极性判断的复信号p(n)相除取虚部,得到误差信号e(n),再经环路滤波器,VCO后对输入信号y(n)进行补偿。所谓极性判决就是根据接收到的符号的极坐标判决到对应对角线上。当极性判决环路锁定大概频偏后便转向DD算法环路进行跟踪并纠正剩余的小频偏。

图1 极性判决算法流程图
1.2 多门限极性判决
传统极性判决算法由于其单一的判决门限导致收敛速度慢锁定误差大等缺陷。对于高阶高码率的QAM信号来说这是不符合需求的。为解决以上缺陷以适应高阶高码率QAM信号,本文采用多门限极性判决。
多门限极性判决[4]的核心思想是增加了锁定误差为零的信号点。在星座图中,根据能量的不同,将信号划分为不同的能量圈。通过降低最外圈门限,可以让更多的信号点通过,但是会引入锁定误差,因此可以通过设定多个门限来多重筛选信号点以逐步锁定相位。
1.3 环路滤波器和VCO结构设计
一阶环路滤波器和VCO组成的二阶环路如图2所示。其中G1和G2为环路滤波器系数,z-1为一个周期延。
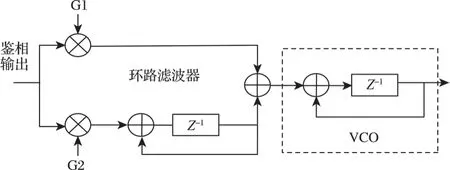
图2 环路滤波器与VCO环路结构
其中系数G1,G2可以通过以下经验公式计算得到:
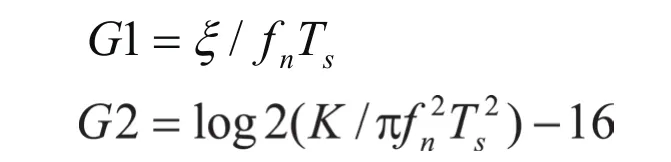
上述公式中ξ为阻尼系数,fn为环路滤波器本振频率,Ts为符号周期。
1.4 极性判决算法模式转换设计
从捕获模式转换到跟踪模式需要有一个转换模块来控制环路的切换[5-6]。模式转换控制有多种方法,可以利用均方误差MSE,也可以根据幅值的平均或根据信噪比的高低为门限来实现转换模式的控制并改变环路滤波器参数的调整。本文采用的是MSE方法来控制模式的转换。下面介绍MSE控制方法的具体设计,图3为实现的流程图。
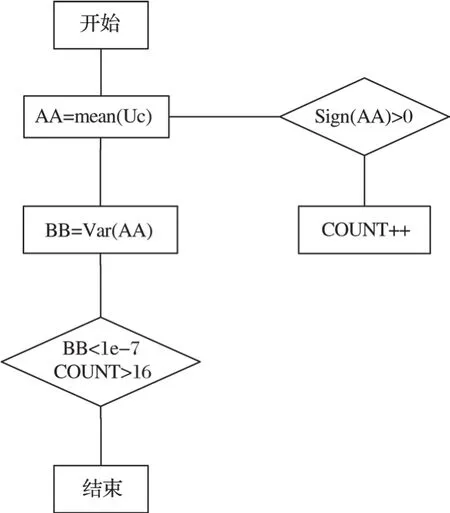
图3 模式转换算法流程图
图3中的Uc是指极性判决环路的环路滤波器输出。我们针对极性判决环路的环路滤波器输出,每64个数据求一个均值,然后对这些均值数据,每32个均值求一次方差,最后针对方差来设置一个门限,这个门限具体可以通过对环路滤波器输出的仿真来求得。同时在这个设计中,我们总共设置两个条件来作为模式切换的条件,其中一个就是针对方差的门限判断,另一个是用于防止假锁出现的均值符号判断。由于均值有可能出现负值而导致假锁现象,所以需要对均值符号做判断,如果每32个均值中超过半数为正值,则断定此次方差门限判决结果有效。通过以上转换控制流程可以准确及时地对模式进行转换。
2 MATLAB仿真结果与分析
首先给出仿真的参数:调制方式为128QAM,采样率为102.4 MHz,信号码速率为25.6 MHz,信噪比为30 dB,对输入信号加入300 kHz的频偏和π/3的相偏,功率检测设置双门限2.2和13.5,仿真点数100 000。同时这里需要给出本文使用的数字接收机[7-8]系统框图以示具体信号流程,系统框图如图4所示。

图4 数字接收机部分系统框图
根据系统框图,我们将定时同步和信道均衡之后的数据作为本文载波恢复仿真的输入数据。
下面我们看载波恢复算法频偏跟踪效果以及星座图。分别如图5与图6所示。
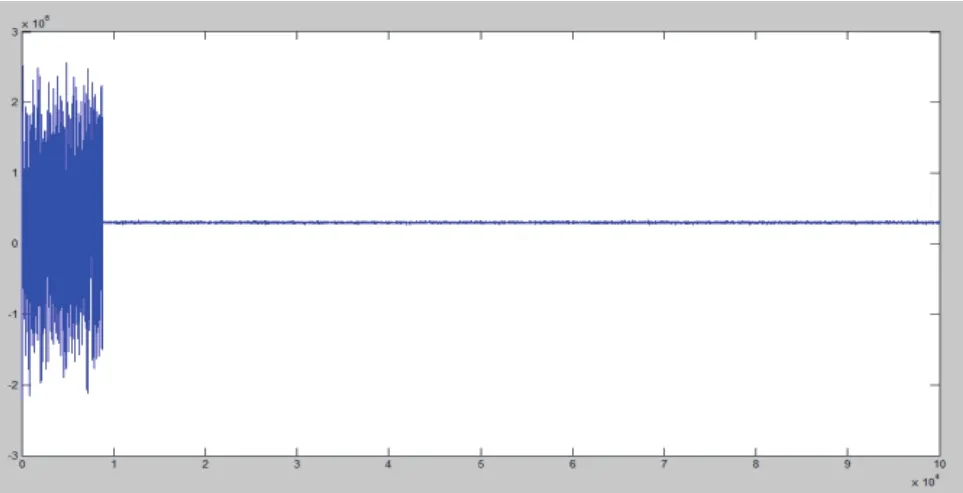
图5 载波恢复频偏跟踪结果
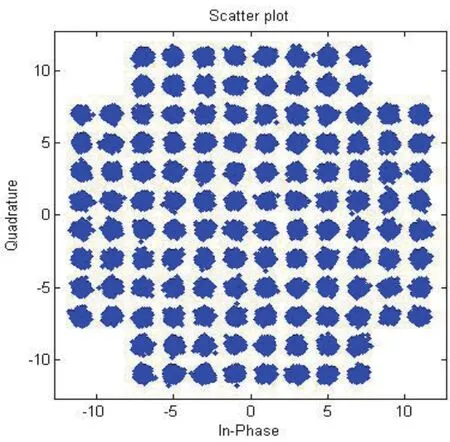
图6 载波恢复后星座图
从上述图中可以看到环路最终锁定效果非常好,频偏稳定在300 kHz左右。并且输出星座点清晰可见,达到了理想的情况。
3 定点仿真与FPGA设计
在FPGA设计实现之前,需要通过定点仿真来限定各个变量的精度,分析有限字长对系统性能的影响,权衡资源消耗和系统性能,从而得出各个信号合适的位宽。
图7为载波恢复算法FPGA实现框图,框图反映了载波恢复算法实现的信号流程以及模块的划分。
算法框图中clk为全局时钟信号,此处为码速率25.6MHz ;reset为系统复位信号;Iin,Qin分别是输入数据的实部虚部;Iout,Qout分别是输出数据的实部虚部。这里所有模块均使用的全局时钟,因为码速率始终不变。cmultip_mult模块为输入信号与VCO输出的复乘模块,在复乘模块之后对应两个环路,分别是极性判决环路和DD算法环路。在捕获阶段系统运行在极性判决环路,首先是经过power_dectect 模块即功率检测模块,然后将判决结果送往鉴相器模块phase_detect_a进行鉴相,之后送往环路滤波器loop_filter_a,对于环路滤波器输出会有一个计算其输出值均方误差的MSE模块,并由MSE模块产生一个环路切换控制信号control。这个控制信号会实现2个控制功能,一个是决定是否转向DD算法环路,另一个是选择输入到VCO模块的数据,即当前所运行环路的滤波器输出数据。当环路切换至跟踪模式时,先进行全星座判决即dd_adjudge模块,然后将判决结果送至鉴相器phase_detect_b,再送交环路滤波器loop_filter_b,之后输出给VCO模块。
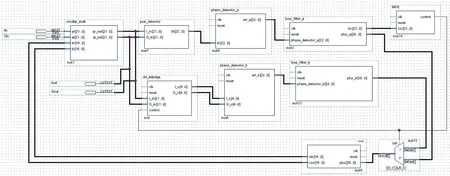
图7 载波恢复算法FPGA实现框图
值得特别说明的是复乘模块与VCO模块,根据算法我们需要将输入数据和VCO做一次复乘运算。这里直接将每个数据分解为实部虚部分别和正余弦值的乘加运算,于是就有:
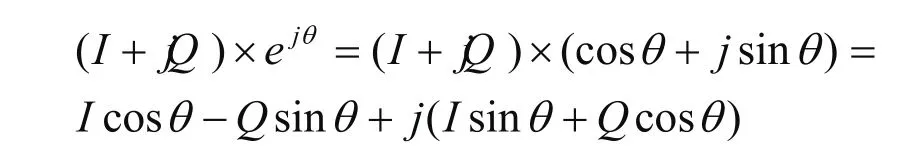
这其中实部虚部均分开单独处理。上式中涉及的正余弦的值通过VCO模块的正余弦查找表来获取。同时由于VCO是进行相位累加运算,最后的相位值必然远大于2π,而我们的正余弦查找表是存储的一个周期的值,因此我们需要在每次累加之后对累加的相位值进行对2π求余。
4 FPGA仿真与调试结果
这里FPGA功能仿真使用QUARTUS软件自带的仿真工具。输入数据采用MATLAB仿真时候的数据源以便对比,这之前需要对其量化。图8为整体的功能仿真图。其中Uc,Ud分别是极性判决环路和DD环路的环路滤波输出,从图中可以看到Ud数据还为0,这是因为环路还没有切换的原因,当环路切换后Uc为0,Ud为对应数据;control_1为环路切换控制信号,当满足环路切换条件时置1,否则为0;phi_vco为相位累加结果,也即正余弦查找表的输入;sin1,cos为查找表结果,并作为复乘模块输入。经综合后该算法结构的资源使用情况如图9所示,可见所消耗的逻辑资源很少。
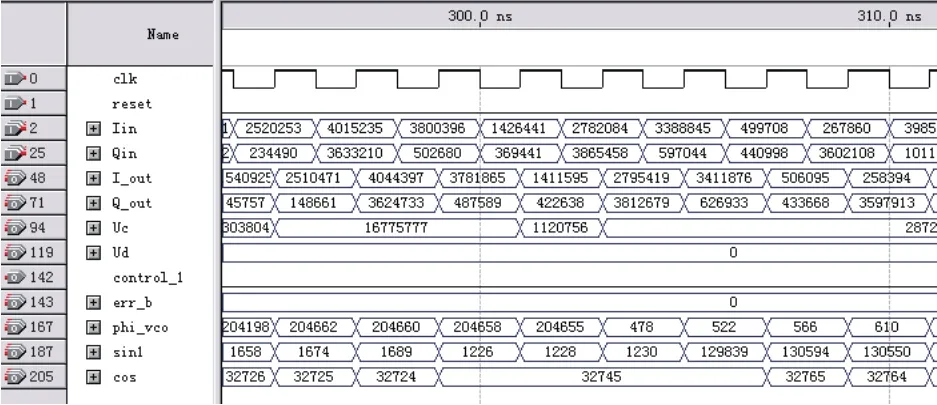
图8 载波恢复算法FPGA整体仿真图

图9 载波恢复算法FPGA资源使用情况
在仿真后我们将需要的仿真结果导入到MATLAB中处理可以得到各个环节的情况。这里给出最后的频率收敛情况(见图10)以及载波恢复后的星座图(见图11)以示设计的效果。从图中可以看到FPGA处理的效果与MATLAB仿真结果基本一致,且星座图效果理想。这说明了本文的FPGA设计是完全符合实际要求的。
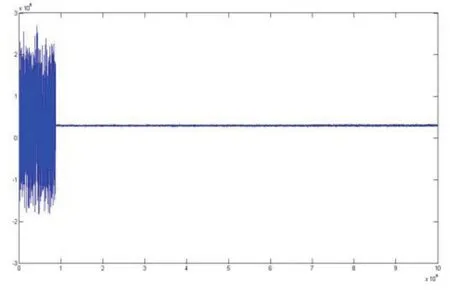
图10 FPGA仿真载波恢复频率收敛曲线
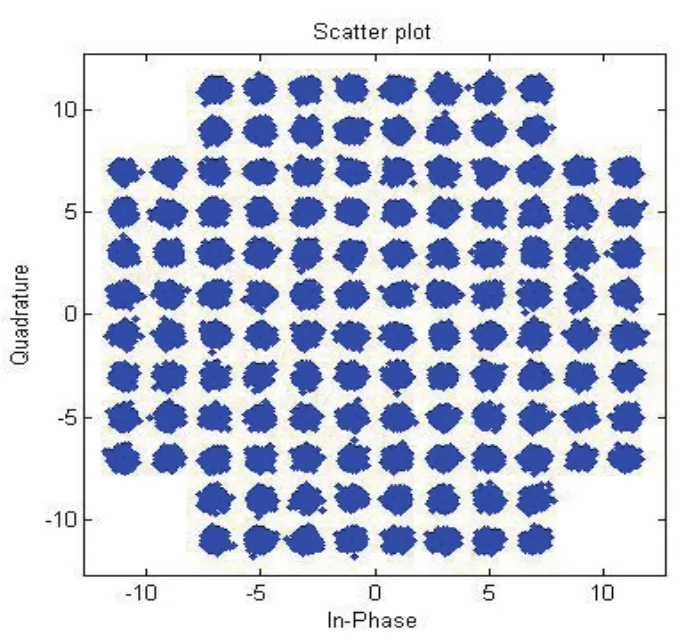
图11 FPGA仿真载波恢复输出星座图
5 结论
本文针对高阶QAM的载波恢复,采用了双模式切换的极性判决算法,并在实际使用中收到了很好的效果。同时,本文针对128QAM设计的FPGA实现方案效果理想,且消耗的逻辑资源很少,最后经过时序约束后运行速率可以达到29 MHz,完全满足系统25.6 MHz的要求。
[1]Kim,Kim-Yun,Choi,Hyung-Jin.Design of Carrier Recovery Algorithm for high_order QAM with large Frequency Acquisition Range[J].IEEE,ICC 2001,Helsinki,Finland,2001, 6:(11-14):1016-1020.
[2]HORIKAWA I,MURASE T,SAITO Y.Design and performances of a 200 Mbit/s 16QAM digital radio system[J].IEEE Trans.Communica-tons,1979,27(12):1953-1958.
[3]刘剑波,牛亚青.QAM调制解调系统中的载波同步算法研究[J].广播与电视技术,2002(7):79-84.
[4]沈丽丽,米亮,葛建华.适合高阶QAM载波恢复算法[J].电视技术, 2003(12):14-17.
[5]胡楠,钟洪声.高阶QAM快速载波恢复电路设计[J].通信技术,2007(11):57-60.
[6]梁海丽,段吉海,游路路.1024QAM调制解调系统的FPGA 实现[J].电视技术,2007,31(4):31-32.
[7]陈祝明.软件无线电基础[M].北京:高等教育出版社:58-124.
[8]周媛,贾怀义.基于FPGA 的全数字64QAM调制解调器设计[J].电视技术,2007,31(S1):40-42.
