石油井下P~t测试仪动态不确定度分析★
2012-09-12王乐裴东兴崔春生
王乐,裴东兴,崔春生
(中北大学 仪器科学与动态测试教育部重点实验室 电子测试技术重点实验室, 山西太原 030051)
0 引言
射孔是油气井勘探与开发过程中最后完井的一项关键技术,由于井下工作环境恶劣且各不相同,对射孔时P~t测试仪的动态参数进行科学的测量显得十分必要。根据专家新提出的新概念动态测试理论,该理论要求测试系统处在被测环境中,跟随被测体一起运动,实时实况地测取被测体的动态参数,也就是说不仅被测量是随时间变化的,测试系统也是处于运动状态且处于恶劣的被测环境中。在动态测量中,测量系统的输入与输出是信号上的对应关系,同静态测量相比,具有时变性、随机性、动态性、相关性等特点。
在该理论的基础之上,本实验中的P~t测试仪的传感器模块选择是ENDEVCO公司的8511系列压阻式压力传感器,标准的测试系统选择的是三个Kistler公司的6213BK型压电晶体高压传感器,电荷放大器为该公司的5015型电荷放大器,同时配套使用成都华采数据采集系统。通过对动态压力数据的测试和数据分析处理,可以明确射孔弹产生的压力曲线,火药的爆燃规律和P~t变化规律[1]。
1 系统数学模型建立及不确定度来源分析
测试系统数学模型的建立要依据系统的工作原理,同时还必须考虑实际工作中其他影响因素,通过修正使其对于输出压力准确度的影响减到最小。石油井下压力测试系统要随同射孔枪放入井底,承受井底高温、高压、高冲击的恶劣环境的作用,引起石油井下压力测试系统的测量结果不确定度的主要因素有:
灵敏度标定引起的不确定度;
温度漂移修正不准引起的不确定度;
加速度效应修正不准引起的不确定度。
2 灵敏度标定引起的不确定度分量
2.1 灵敏度标定
首先,在工作量程内合理选择4或5个动态压力脉冲峰值为校准点,进行多次校准。其次,将3套标准系统各校准点的输出值P0,P1,P2的平均值P作为该点脉冲峰值的最佳估计值,依据公式(2)计算出该校准点灵敏度系数K:
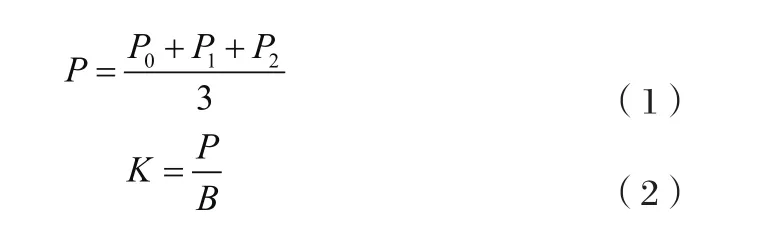
式中,B:标定系统软件读出值,为校准点脉冲峰值对应的数字量,bit。
对P~t测试仪进行了4次标定,表1为一次校准记录的数据。最后的灵敏度系数取4次标定的平均值为:y=0.0503x。方程的线性度R2=0.9999。
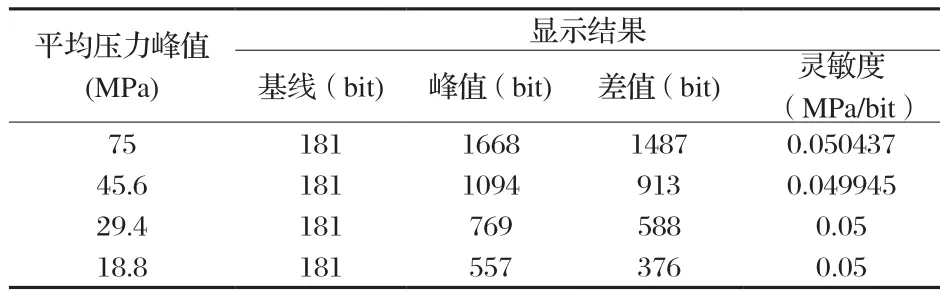
表1 一次校准数据
2.2 测量不确定度来源
1)3通道标准测压系统的压力幅值平均值测量不确定度分量urel(P)
引起标准测压系统测量结果不确定度的分量有:标准传感器和电荷放大器、多通道数据采集卡、标准压力源。在204所,采取全系统静态校准方法对3套测压系统进行静态校准,ch0,ch1,ch2分别代表3套标准系统,得出标准测试系统的不确定度如表2所示。

表2 标准测试系统的不确定度数据
3通道压力幅值测量平均值的相对不确定度为urel(P):
2)测试系统灵敏度多次标定重复性引入的不确定度uAel(K)
在量程范围内选择几个半正弦压力脉冲峰值为校准压力点,如表3~6所示为对测试系统重复进行4次灵敏度校准记录的数据。

表3 第一次校准数据

表4 第二次校准数据

表5 第三次校准数据
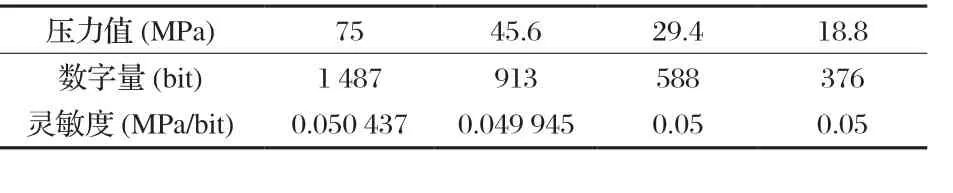
表6 第四次校准数据
利用贝塞尔法计算出每次校准灵敏度平均值的相对不确定度,当四次重复校准动态灵敏度系数平均值的实验标准差没有明显的差异和规律变化,可以采用合并各区间的样本标准差得出自由度比较高的测试系统灵敏度重复性不确定度uArel(K)。

2.3 分辨率引起的测试系统数字量输出值不确定度urel(B)
由于被测信号经过A/D转换成数字量,A/D为12位,则相对不确定度为:
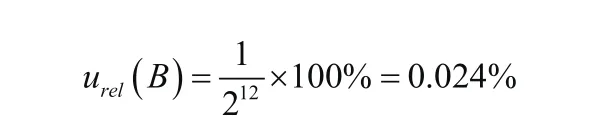
测试系统灵敏度合成相对标准不确定度为ucrel(K)
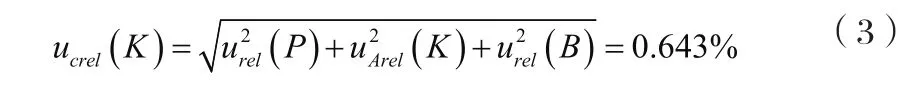
3 温度漂移修正不准引起的不确定度分量
为了确定由环境温度变化引起的测试系统不确定度分量,将传感器放入高低温恒温箱,温度变化范围-40℃~+140℃,每隔20℃由高精度电压表记录1次传感器输出值,并且在每个温度点上恒温2个小时,按照上述方法进行3次实验,记录的数据见表7。
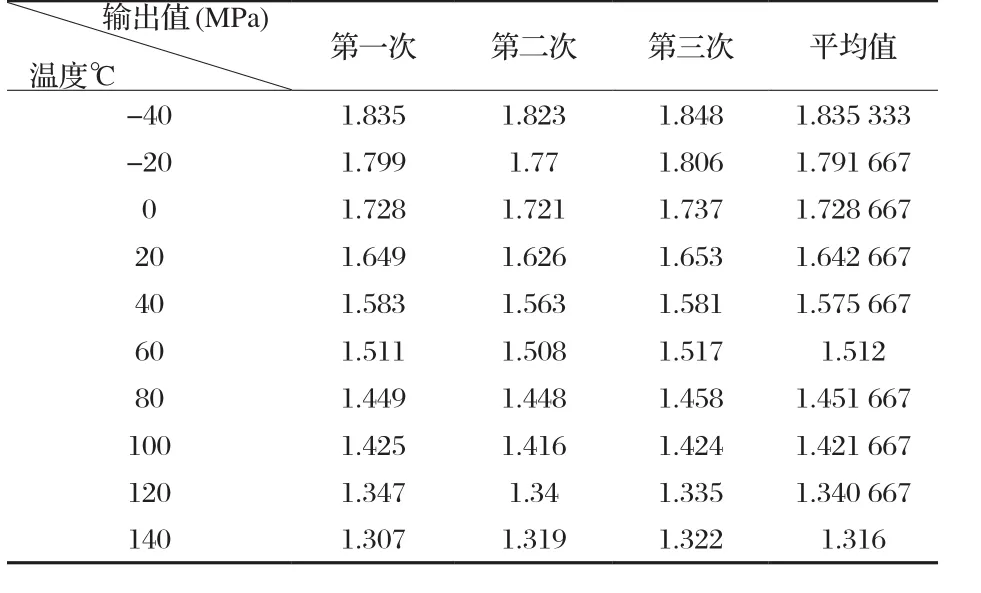
表7 传感器高低温实验数据
为了保证实验精度,每个温度点上3次实验的平均值作为各个温度点的输出值,求出工作曲线的a1,a2和R2值,a1=1.713 2,a2=-0.003,R2=0.991 5。根据R2的值,可看出T与P(T)呈线性关系,其回归直线方程为:
PT=1.713 2-0.003T。
采用最小二乘法求出a1,a2的标准不确定度:

拟合曲线引入的合成不确定度为:
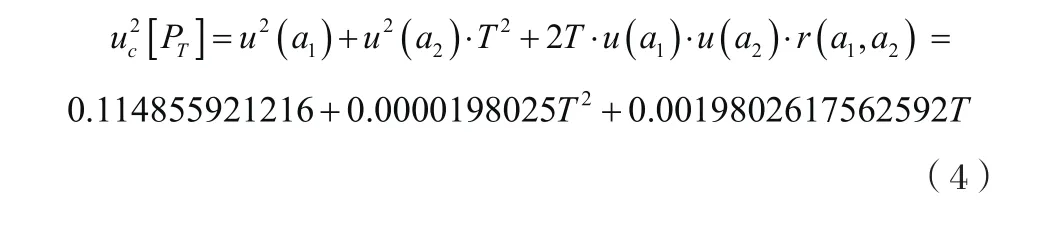
4 加速度效应修正不准引起的不确定度分量
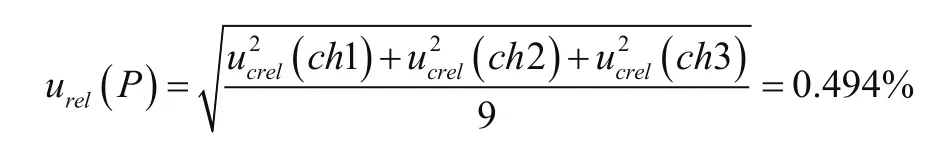
在马歇特锤实验机上进行了传感器的加速度冲击实验,通过改变落锤高度给出不同大小的加速度值进行多次实验,记录加速度传感器波形峰值对应的加速度值a和压力传感器输出波形的峰值对应的压力值P(a),实验数据如表8所示。

表8 加速度校准实验实测数据
用最小二乘法原理求出校准曲线的b1,b2和R2值:b1=-0.257 6,b2=0.000 5,线性度R2=0.998 5,其回归直线方程为:
Pa=0.000 5a-0.257 6。
依据最小二乘法原理计算b1,b2的标准不确定度:
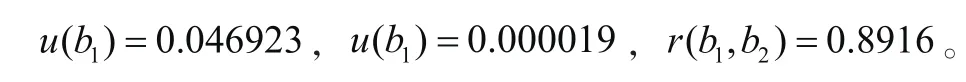
拟合曲线引入的合成不确定度为:
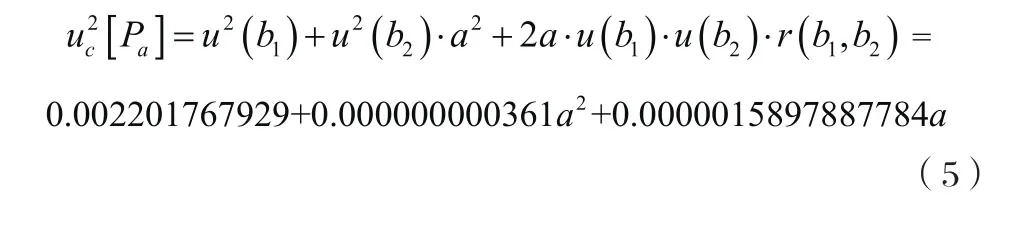
5 结论
通过对测量过程中所产生的各分量值的仔细分析,计算得出该P~t测试仪测试系统灵敏度合成相对标准不确定度为0.643%,根据新概念动态测试理论,要求测试系统处在被测环境中,跟随被测体一起运动,实时实况地测取被测体的动态参数,为此温度漂移修正不准引起的不确定度以及加速度效应修正不准引起的不确定度是分别随着温度和加速度的变化而变化的。因此,传感器温度从-40℃变化到+140℃,其温度漂移修正不准引起不确定度如式(4)所示,加速度效应修正不准引起的不确定度如式(5)所示。
[1]陈喜庆.复合射孔工艺技术研究[D].大庆:大庆石油学院,2008.
[2]王华,祖静,杨志刚.石油井下电子测压器的新发展[R].中国兵工学会第六届测试技术学术年会论文集,1992:374-353.
[3]成建龙,周志华,乔晓光.复合射孔器动态压力测试方法研究[J].测井技术,2005(29):55-59.
[4]王中宇,夏新涛.测量不确定度的非统计理论[M].北京:国防工业出版社,2000:43-60.
[5]谢少锋,代大山.动态不确定度及其在测量系统中的应用[J].中国计量,2005(1):5-76.
[6]中国计量测试学会压力专业委员会.压力测量不确定度评定[M].北京:中国计量出版社,2006:30-264.
[7]樊尚春.压力测量不确定度评定基础知识讲座[J].测控技术,2009(28):90-94.
[8]宋明顺.测量不确定度评定与数据处理[M].北京:中国计量出版社,2000:23-159.
[9]张衍芳,杜红棉,祖静.压力测试系统修正方法的研究[J].电子测试,2011(2):47-51.
