岩石介质的分形空隙模型及其维数解析❋

王鲜霞,王彩贤,隋丽丽

(1.太原理工大学 数学学院,山西 太原 030024;2.华北科技学院 基础部,北京 101601)

分形几何学是近几十年发展起来的处理“不规则”及复杂系统的一门数学学科,结合诸多工程技术领域的自相似问题,应用极其广泛.岩石是一种具有严重初始损伤的复杂的地质材料,岩石结构中缺陷杂乱无章,随机分布,在载荷等外部作用下,他们不断萌生、扩展、聚集、贯通,最终导致岩石的宏观破碎.从20世纪 80年代起,已有较多的研究表明,岩石结构中细观缺陷的尺度分布,裂缝的生成及扩展,岩石节理面,岩石断裂表面的粗糙性,岩石破碎的块度分布等均具有较强的分形特征[1-7],对于裂缝的维数,裂缝的动静态扩展,文献 [5,7]中均有研究.但对于分形的初始损伤并没有做太多的研究.本文在前人研究的基础上,构造出了一种更接近实际情况的岩石初始结构的分形空隙模型,并进一步研究了它的维数与破碎后块度分布维数的关系.

1 分形维数基本理论[8-11]

1.1 Hausdorff维数

定义 1 设 S≥0,W＞ 0,F是 Rn上一任意子集.令是 F的 W-覆盖 },若存在或为无穷大,则称Hs(F)为 F的 s维 Hausdorff测度.

定义 2 称数 dimHF=inf{s：Hs(F)=0}=sup{s：Hs(F)=∞}为 F的 Hausdorff维数.

1.2 盒维数

定义 3 设 F是 Rn上的任意紧子集,NX(F)表示覆盖 F的直径为X＞0的闭球的最少个数,如果存在,则称该极限为集 F的盒维数,记为

1.3 自相似维数

若一个集合 F由 N个与它相似的部分组成,且相似比为 r,则认为 F为自相似集.如三分Cantor集,Von koch曲线,Sierpinski垫均为自相似集.

定义 4 设 F是 Rn上的有界子集,如果 F可以分成 N＞1个相等的且与 F相似的部分,则称F为自相似集,且如果每部分与 F的相似比为则称 D为自相似集 F的自相似维数,记为

Hausdorff维数是建立在测度概念的基础上的,因此它对任意集都有定义,但在实际应用中难以计算;盒维数较 Hausdorff维数更便于计算,但它有可能不存在,也没有相应的测度支持,这会给它的理论发展带来一些困难;自相似维数只对特殊的严格自相似分形集成立,在实际事例中其应用有局限性,主要体现在这种自相似性只是在近似或统计意义下成立.但事实上很多理论都来源于统计意义下的近似实际,因此对于实际事例,常常采用统计自相似维数.

综上比较,还是统计自相似维数应用最广泛,也较为简单.岩石介质的空隙结构就具有这种统计自相似性,因而可以用统计自相似分形理论来探究.

2 岩石介质的分形空隙模型的建立与维数解析

2.1 对已有模型的讨论

目前,已有许多分型模型[12-13]被用来模拟这种随机矿物的扩展,进而分析岩石的空隙结构.多孔介质的空隙分布具有分形结构,因此可用分形模型来定量描述.机理是利用分形的构造过程,即对初始元反复复制生成的原理,模拟多孔介质中空隙和粒子的空间结构以及粒子的扩散和聚集.最常见的模型有以下 3种：

1)传统的 Koch岛模型.即可将 3条或更多的 Koch曲线连接起来,组成一个封闭的 Koch岛.经过 n次迭代后,这种分形构造的边长为

式中：

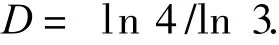
2)Sicrpinski垫片模型.此模型的做法是：假设初始边长为L的等边三角形是一个光滑的岩石空隙,而每步去掉的中心小三角形可看作是越来越小的矿物晶粒不断地充填到这个初始空隙空间.在这样的 n次演变后,空隙空间仅由尺寸为 r=L/2n的三角形组成.这样的小三角形的数目满足

其空隙率为

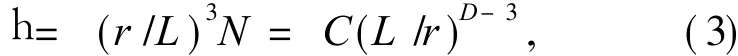
式中：D=ln 3/ln 2;C为常数;L和 r分别为空隙尺度的上限和下限值.

3)Menger海绵模型.此模型的构造是：取一个正六面体为初始元,将他的 6个面均作 9等分,这等价于将正六面体进行 27等分,然后去掉体心与面心处的7个小立方体.将上述操作重复下去,直至无穷,将得到Menger海绵模型.分维值D=2.7768[12].此 Menger海绵模型的构造思想可以用来模拟岩土粒子的空隙特性.

以上空隙介质的数学分形模型确实表示了岩石分形空隙的统计平均性,并且分维D总是在2和3之间.目前已有一些试验结果[7]证实了上述分形描述的可行性,但是模型1与2均是在平面上讨论问题,模型 3虽然是在三维空间中的体积模型,但这些模型均太理想化,实际岩石的空隙具有随机的表面和体积分形特征.所以本文在这些模型的基础上进行改造,构造了一种更接近实际的岩石介质分形空隙随机模型.

2.2 岩石介质的分形空隙随机模型及维数解析

为了模拟多孔介质中空隙的空间分布状况,本文在 Menger海绵模型的基础上,加入概率的思想,构造出了一个更贴近实际岩石空隙结构的分形模型.具体做法如下：

1)假设初始元的直径为 R,个数为1个.

3)在每次产生的小块体中去掉的概率为定值p.

按此方法构造下去,则1次后产生的个数为

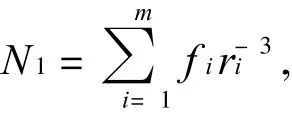
留下的个数为

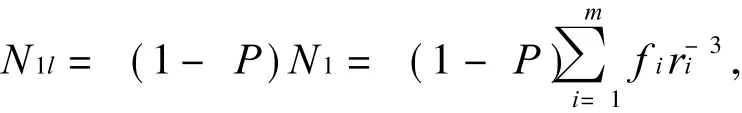
去掉的个数为

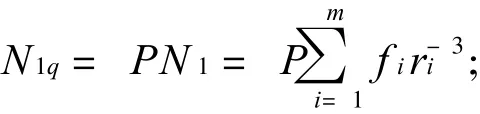
2次后产生的个数为

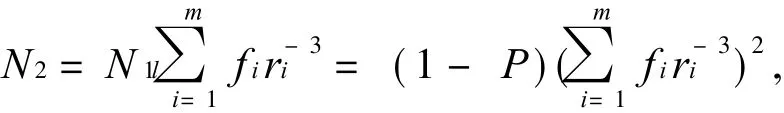
留下的个数为

第一方面是确定药剂类型和投加量，通过试验选择适宜的药剂并确定其最佳投加量，在降低使用成本的同时，发挥其最大功效。

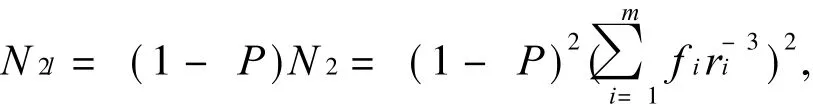
去掉的个数为

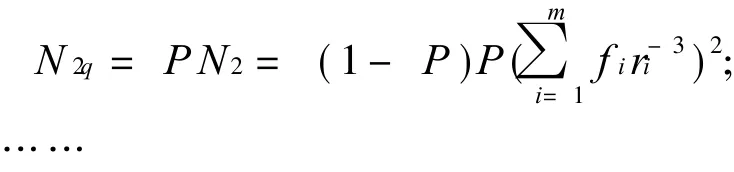
k次后产生的个数为

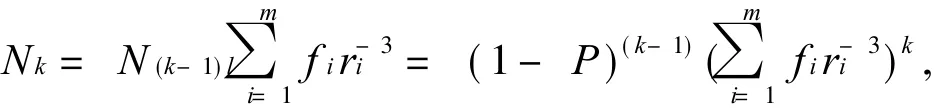
留下的个数为

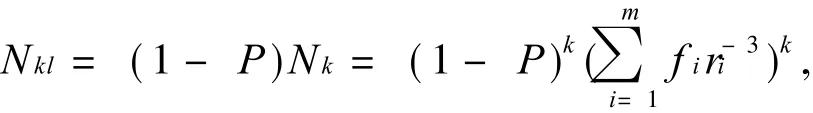
去掉的个数为

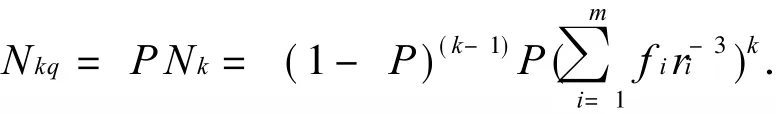
则由分形维数的公式可知

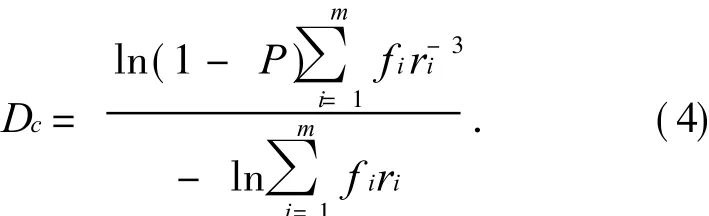
为了运算简单仍然以相似比的数学期望和直径的数学期望来代替它们的平均值,因此公式(4)可简化为

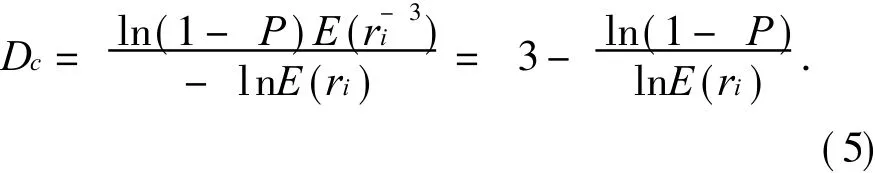
由公式(5)可知

1)分形维数 D随着 P的增大而减小(E(ri)一定),也随着 E(ri)的增大而减小(P一定).

2)由实际情况可知,P≪1,0＜E(ri)＜1.那么,则 k次后样本中剩余的体积 Vl为

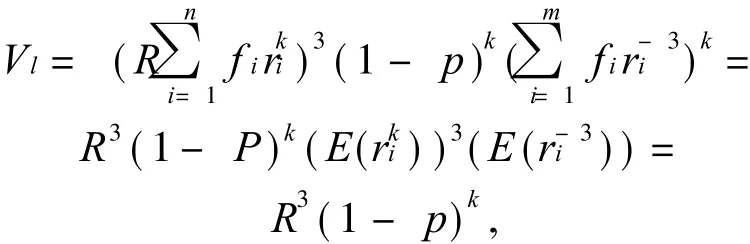
空隙体积 Vh为

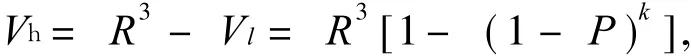
则空隙率h为

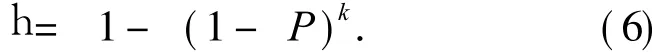
这样的话,空隙率就会随着 P的增大而增大.

3 岩石初始结构与破碎相关性的分形分析

岩石宏观破碎是其内部缺陷不断萌生发育、扩展、聚集和贯通的最终结果[14-15],这个从细观损伤发展到宏观破碎的过程是因自身重力的影响或受外力的作用使得岩石中大量的、各种尺度的空隙切割、贯通所产生的,故岩石初始损伤的分布状况与岩石破碎块度的分布有着直接的相关性.

由文献 [15]中的公式

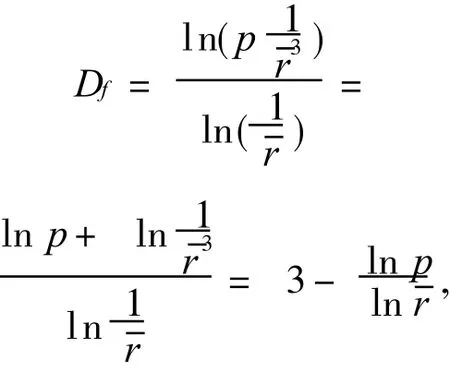
与公式(5)可得到以下结论：

初始结构中 p越大,空隙率h就越大,结构中空隙的分布维数 Dc就越小,岩石在受到外力作用下时就越容易破碎,也就是说破碎的概率就越大.这样的话,破碎块度的分布维数 Df就越大.可见,初始结构的分布维数 Dc与破碎后块度的分布维数 Df之间存在着负相关的关系.

4 结束语

从分形几何学的角度建立了岩石初始结构的分形空隙模型,并通过随机破碎个数与自相似比的数学期望,给出了其自相似维数的解析公式.本文对该维数与破碎后块度的分布维数进行了分析研究,得出了二者之间存在负相关关系的结论,为采场岩层移动变形规律的研究提供了全新的思路与理论指导.

[1][英]法尔科内著.分形几何——数学基础及其应用[M].曾文曲,刘世耀,戴连贵,等译.北京：人民邮电出版社,1991：41-70,155-156,290-297.

[2]Falconer J.Fractal Geometry：Mathematical Foundations and Applications[M].New York：John Wiley and Sons,1990：10-30.

[3]Mandelbrot B B.The Fractal Geometry of Nature[M].New York： Freeman,San Francisco,1982：95-190.

[4]Hausdorff F.Dimension and ausseres mass[J].Math.Annalen,1919,79：157-179.

[5]冯国瑞.长壁开采上覆岩层损伤范围及上行开采的层间距分析[J].煤炭学报,2009,34(8)：1032-1036.Feng Guorui. Analysison thedamage zone of overlyingstrata and safety layer distanceon the upward mining above the longwall goaf[J].Journal of China Coal Society,2009,34(8)：1032-1036.(in Chinese)

[6]冯国瑞.煤矿残采区上行开采基础理论与实践 [M].北京：煤炭工业出版社,2010.

[7]冯国瑞,张绪言.刀柱采空区上方遗弃煤层上行开采可行性判定 [J].煤炭学报 ,2009,34(6)：726-730.Feng Guorui, Zhang Xuyan. Feasibility on the upward mining of the left-over coal above goaf with pillar supporting method[J].Journal of China Coal Society,2009,34(6)：726-730.(in Chinese)

[8]冯国瑞,仲丛明,任亚峰,等.地下空间开挖过采空区时覆岩移动变形的数值模拟研究[J].隧道建设,2011,31(4)：453-456.Feng Guorui,Zhong Congming,Ren Yafeng,et al.Numerical simulation on displacement of rock cover when excavation above goaf[J].Tunnel Construction,2011,31(4)：453-456.(in Chinese)

[9]孙洪泉,谢和平.岩石断裂表面的分形模拟 [J].岩土力学 ,2008,29(2)：347-352.Sun Hongquan,Xie Heping. Fractal simulation of rock fracture surface[J].Rock and Soil Mechanics,2008,29(2)：347-352.(in Chinese)

[10]陆冰洋.岩石类材料损伤演化的分形几何行为特征及其分形机理研究 [D].贵阳：贵州大学,2007.

[11]谢和平.分形几何及其在岩土力学中的应用[J].岩土工程学报,1992,14(1)：14-24.Xie Heping.Fractal geometry and its application to rock and soil materials[J]. Chinese Journal of Geotechnical Engineering,1992,14(1)：14-24.(in Chinese)

[12]于广明.地下开挖影响下岩体分形性质演化问题探讨 [J].岩石力学与工程学报,2004,23(s2)：4674-4678.Yu Guangming.Advanceand prospect in research of evolution of factal characteristics of rock mass caused by underground mining[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(s2)：4674-4678.(in Chinese)

[13]高峰.岩石损伤和破碎相关性的分形分析 [J].岩石力学与工程学报,1999,18(5)：497-502.Gao Feng.Fractal analysis of the relation between rock damage and rock fragmentation[J]. Chinese Journal of Rock Mechanics and Engineering,1999,18(5)：497-502.(in Chinese)

[14]谢和平.岩石断裂和破碎的分形研究[J].防灾减灾工程学报,2003,23(4)：1-9.Xie Heping.Fractal fracture and fragmentation in rocks[J].Journal of Seismology,2003,23(4)：1-9.(in Chinese)

[15]王鲜霞.冒矸破碎分形模型的建立与维数解析[J].太原理工大学学报,2008,39(5)：530-532.Wang Xianxia.Establishment of the fractal model aboutwaste rock fragmentation and dimension analysis[J]. JournalofTaiyuan Universityof Technology,2008,39(5)：530-532.(in Chinese)