模糊关系各种性质的迹的刻画❋

张彩霞,王绪柱

(太原理工大学 数学学院,山西 太原 030024)

模糊关系[1]在模糊决策的许多领域都有非常重要的作用.模糊关系各种性质主要有 T-传递、S-强完全和 T-S-Ferrers等.Fodor在文献 [2]中对这些性质进行了讨论,并揭示了这些性质之间的联系.随后,Fodor又在文献 [3]中用迹刻画了模糊关系的绝大多数性质,但他在文献 [3]中所得到的很多结论都是在(T,S,N)为强 De Morgan三元组时才成立.这是个很强的条件,它要求所涉及的 t-模及 t-余模分别为 Lukasiewicz t-模及 t-余模[4]的同构变换.因此,本文在其它 t-模及 t-余模的情况下,讨论了一些模糊关系性质的刻画问题.例如对 T-S-Ferrers性质证明了当T=Tmin,S=Smax时,若 Rl完全,则 R为 T-SFerrers关系成立;同时本文还给出了 S-强完全性的一个等价条件等.

1 预备知识

定义 1 设 T是一个 t-模,记 IT(x,y)=sup{z|T(x,z)≤y},称 IT是由 t-模 T导出的蕴涵.

引理 1 对任意连续 t-模 T,IT具有下列性质：∀x,y,z,t∈ [0,1].

1)T(x,z)≤ y⇔ IT(x,y)≥ z;

2)IT(x,z)≤ IT(x,y)≤ IT(t,y),当 z≤ y,t≤ x时 ;

3)IT(x,y)=1⇔ x≤ y.

引理 2 当(T,S,N)为强 De Morgan三元组时,S(N(x),y)=IT(x,y).

定义 2 设 R1,R2是 A上的模糊关系,T是t-模,S 是 t-余 模. 定 义 R1和 R2的 T-合 成R1˚TR2为 ∀a,b∈ A,(R1˚TR2)(a,b)=

定义 3 设 R是 A上的模糊关系,定义 R的左迹 Rl和右迹 Rr分别为

定义 4 设 T为 t-模,S为 t-余模,R为 A上的模糊关系.模糊关系的各种性质定义如下：

1)若 ∀a,b∈ A,S(R(a,b),R(b,a))=1,则称 R为 S-强完全的.特别地,当 S=Smax时,S-强完全简称为强完全;

2)若 ∀a,b,c,d∈ A,T(R(a,b),R(c,d))≤S(R(a,d),R(c,b)),则称 R是一个 T-S-Ferrers关系.特别地,当 T= Tmax,S= Smax时,T-SFerrers关系简称为 Ferrers关系.

2 主要结论

定理 1 当(T,S,N)为强 De Morgan三元组时,下列 3个陈述等价：

1)R为 S-强完全;

2)Rd˚TRl⊆ R;

3)Rr˚ TRd⊆ R.

证明 1)⇔ 2).若要证明 Rd˚TRl⊆R成立,等价于证明对任意的 a,b,c∈ A,sucp T(Rd(a,c),Rl(c,b))≤R(a,b).也就是等价于证明对任意的a,b,c∈ A,T(Rd(a,c),Rl(c,b))≤ R(a,b),也等价于证明 T(Rd(a,c)(R(a,c),R(a,b))≤R(a,b).由引理 1中的 1)知,上式等价于证明

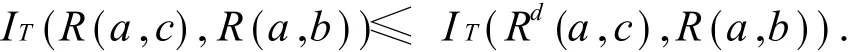
事实上,由于 R满足 S-强完全性,故∀a,c,S(R(c,a),R(a,c))=1.由(T,S,N)为强 De Morgan三元组,则由引理 2可知,IT(N(R(c,a)),R(a,c))=S(R(c,a),R(a,c))= 1,则Rd(a,c)≤R(a,c).故由引理 1中的 2)知,IT(R(a,c),R(a,b))≤IT(Rd(a,c),R(a,b)),则对任意的 a,b,c∈A,,Rl(c,b))≤ R(a,b),即Rd˚TRl⊆ R.

2)⇐1).由 Rd˚TRl⊆R可知,对任意的 a,b,c∈A,,Rl(c,b))≤R(a,b).由 a,b,c的任意性知,T(Rd(a,b),Rl(b,b))≤R(a,b),即T(Rd(a,b),1)≤R(a,b),则 Rc(b,a)≤R(a,b).

根据(T,S,N)为强 De Morgan三元组,则由引理 2知,∀a,b,S(R(b,a),R(a,b))=IT(N(R(b,a)),R(a,b))=IT(Rc(b,a),R(a,b))=1,故 R为 S-强完全的.

1)⇒3).证明过程类似于 1)⇒2).

3)⇐1).证明过程类似于 2)⇐1).

综上所述,可知 1),2),3)等价.

定理 2 若 Rl是强完全的,则 R为 Ferrers关系.

证明 由 Rl强完全可知,∀a,b,Rl(a,b)=1或 Rl(b,a)=1.分两种情况讨论：

1)当 Rl(a,b)= 1时,对 ∀c,IT(R(c,a),R(c,b))=1⇔∀ c,R(c,a)≤ R(c,b)⇒ R(c,a)≤R(c,b)∨ R(d,a).

2)当 Rl(b,a)=1时,对 ∀d,IT(R(d,b),R(d,a))=1⇔∀ d,R(d,b)≤ R(d,a)⇒ R(d,b)≤R(c,b)∨ R(d,a).

由 1),2)可知 ,R(c,a)≤ R(c,b)∨ R(d,a)或 R(d,b)≤R(c,b)∨ R(d,a),则对任意的 a,b,c,d,R(c,a)∧ R(d,b)≤ R(c,b)∨ R(d,a). 因此 ,R为 Ferrers关系.但是,当 R是 Ferrers关系时,不一定能得到 Rl是完全的.例如令 R=,容易验证R为 Ferrers关系.但经计算可得Rl=.很明显,Rl不是完全的.

[1]Wang Xuzhu,Ruan Da,Kerre E E.Mathematics of Fuzziness-Basic Issues[M].Springer-Verlag,2009.

[2]Fodor J,Roubens M.Fuzzy Preference Modeling and Multicriteria DecisionSupport[M].Kluwer Academic Publishers,Dordrecht,1994.

[3]Fodor J.Traces of fuzzy binary relations[J].Fuzzy Sets and Systems,1992,50：331-341.

[4]Klement E P,Mesiar R,Pap E.Triangular Norms[M].Kluwer Academic Publishers,2000.

[5]Baczynski M.(S,N)-and R-implications,a state-ofthe-art survey[J].Fuzzy Sets and Systems,2008,159：1836-1859.

[6]Xue Ye,Wang Xuzhu.The transitivity-related properties of operations of fuzzy relations[J].Journal of Taiyuan University of Telechnology,2003,34(1)：56-59.

[7]Peng Yuwei,Xu Xiaozhan.The dual composition of fuzzyrelations and its applicationstotransitivity properties[J]. Fuzzy Systems and Mathematics,2005,19(4)：54-59.

[8]De Baets B,Van de WalleB,KerreE.Fuzzy preference structures without incomparability[J].Fuzzy Sets and Systems,1995,76：333-348.

[9]Trillas E,Valverde L. On some functionally expressable implications for fuzzy set theory[J].Seminar on Fuzzy Set Theory,1981,3：173-190.

[10]Gaines B R. Foundations of fuzzy reasoning[J].Man-Machine Study,1976,6：623-668.