基于拓扑和尺寸组合优化的ATV车身轻量化研究❋

卢建志,杨世文,李 鹏,任子清

(1.中北大学机电工程学院,山西太原 030051;2.长安新能源汽车北京研发中心,北京 100081;3.国营六一六厂铸造厂,山西大同 037036)

0 引 言

车辆的车身质量占总质量的 40% 左右,车身的轻量化对整车的轻量化起着举足轻重的作用,车辆的轻量化正成为 21世纪车辆技术的前沿和热 点[1].目 前 ComputerAidedEngineering(CAE)技术在车辆车身设计、分析与优化中的应用越来越广泛.文献 [2]中基于 Ansys软件对ATV车架进行了各个部件的尺寸优化,优化后车架的最大应力减少了 11.95%,车架的质量减少了 28.97%.文献 [3]以壳单元为基础,建立了ATV(全地形车)车架的有限元模型,选择满载状态下的典型工况,计算了车架的强度和刚度,进行了模态分析;并通过道路可靠性试验,验证了分析结果的正确性,提出了结构改进方案.文献[4]中提出了一种形状和尺寸组合优化方法,通过分离设计变量,分别采用渐进节点移动法和满应力法优化桁架结构的形状和尺寸;通过循环迭代,耦合形状和尺寸变量间的相互作用关系,得到了结构的最小重量.在文献 [5]中,P.S.Tang和 K.H.Chang提出了利用几何重构技术,集成拓扑和形状优化技术,从而得到光滑的几何边界和易于加工的几何模型的方法.首先将拓扑优化几何转换成光滑的参数化的 B样条曲线和曲面,然后曲线曲面导入到参数化的 CAD环境中建立结构的实体模型,再对结构进行形状优化.

文中提出的组合优化方法,能够在概念设计阶段对车辆的车身结构同时进行车身蒙皮的尺寸优化和骨架的拓扑优化设计,并以 ATV车身的结构优化为算例,对比了原车和组合优化方法得到的有限元分析结果,验证了该方法的可行性.文中有限元建模采用 Hypermesh软件,结构优化使用的软件是 Optistruct.

1 拓扑优化和尺寸优化方法

1.1 基于密度法的材料插值拓扑优化方法

从 20世纪末期以来,产生了许多拓扑材料插值理论和拓扑结构描述方法,其中均匀化方法和密度法材料插值模型最具有代表性.目前在工程拓扑优化问题的求解中很少采用均匀化方法,较多采用密度法材料插值模型.

密度法以连续变量的密度函数形式表达单元相对密度与材料弹性模量间的对应关系,这种方法是基于各向同性材料,不需要引入微结构和附加的均匀化过程,它以每个单元的相对密度作为设计变量,人为假定相对密度和材料弹性模量间的某种对应关系,程序实现简单,计算效率高,是从均匀化方法发展而来的一种方法[6].

1.2 尺寸优化

对结构优化设计最简单和最直接的做法就是修改结构单元的尺寸.尺寸优化中的设计变量可能是杆的横截面积、惯性矩、板的厚度,或是复合材料的分层厚度和材料铺层角度.在用有限元计算结构位移和应力时,尺寸优化过程不需要网格重新划分,直接利用灵敏度分析和合适的数学规划方法就能完成尺寸优化.对于具有连续性结构的板或壳,也只是把各单元厚度作为设计变量,优化结果是阶梯形分布的板厚度或壳厚度.在这类优化过程中,设计变量与刚度矩阵一般为简单的线性关系.尺寸优化技术经历了 20多年的研究,重点主要集中在优化算法和灵敏度分析的研究[7].

2 拓扑和尺寸组合优化模型

ATV(全地形车)车身结构主要由车身蒙皮、车身骨架、座椅等组成.在车身的概念设计阶段,通常采用类似于文献 [5]中的设计方法：先确定载荷传递路径,再进行详细的尺寸设计的阶段优化方法对车身进行轻量化设计.这种常用的轻量化方法虽然可以得到结构的加载路径和详细的优化尺寸,但是得到的拓扑优化结果往往出现不连续、材料堆积等现象,而且整个概念设计至少需要二次的 CAD,有限元建模和优化计算过程;由于ATV车身结构尺寸比较大、形状复杂,这种阶段优化方法花费了大量的时间,加大了产品的时间成本,大大降低了所研发车身的市场竞争力.

本文引入拓扑和尺寸组合优化方法,该方法分别以车身蒙皮的厚度和车身骨架的密度作为车身蒙皮尺寸优化设计变量和车身骨架的拓扑优化设计变量,以车身整体的刚度为约束条件,以尺寸和拓扑优化区域的总质量为目标函数;耦合拓扑变量和尺寸变量之间的关系,得到最优的载荷传递路径和蒙皮尺寸厚度.组合优化设计方法的流程如图 1所示.

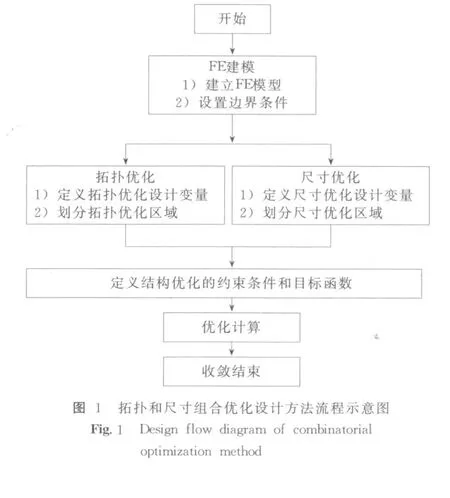
如图 1所示,整个组合优化设计可以分为拓扑优化和尺寸优化两个子模块,得到拓扑和尺寸设计变量的耦合变量,下面分别对这两个模块作简单介绍.

2.1 拓扑优化模块

拓扑优化模块采用当前拓扑优化中常用到的基于密度法的材料插值模型,其数值模型如下：

式中：di是单元密度;f(d)是拓扑优化区域的目标函数;G(di)≤Gmax是约束条件.

2.2 尺寸优化模块

尺寸优化模块的数学模型如下：

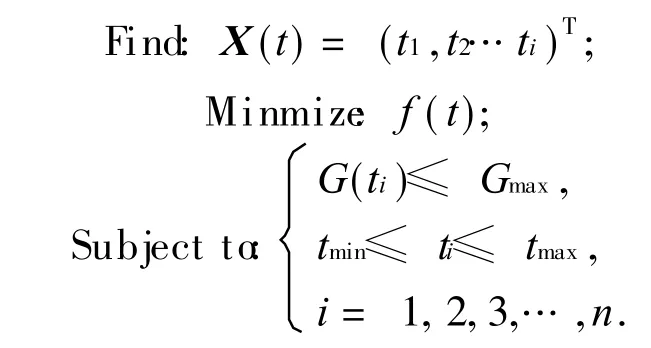
式中：ti为车身单元的厚度;f(t)是尺寸优化区域的目标函数;G(ti)≤Gmax是约束条件;tmin,tmax是许用的最小、最大厚度尺寸.

2.3 拓扑和尺寸组合优化模型

由以上组合优化的两个子模块的数学模型很容易得到拓扑和尺寸组合优化的数学模型：

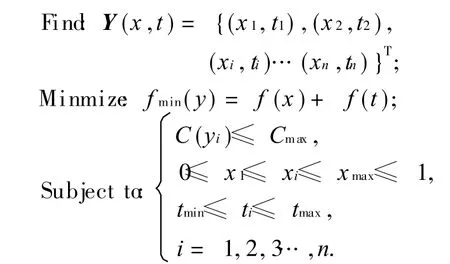
式中：密度 xi为拓扑优化设计变量;车壁厚度 ti为尺寸优化设计变量;Y(x,t)为组合优化的耦合变量;fmin(y)是组合优化的目标变数;f(x)和 f(t)分别为拓扑和尺寸优化区域的子目标函数;C(yi)≤Cmax为组合优化的约束条件;tmin,tmax分别为尺寸优化时的最小允许尺寸和最大允许尺寸.

在 optistruct结构优化软件中,可以同时定义拓扑优化设计变量和尺寸优化设计变量,定义车身蒙皮和车身骨架的总质量最小为目标函数.

3 ATV车身的拓扑和尺寸组合优化设计

3.1 车体材料

车体材料采用装甲钢板,材料的弹性模量为208 GPa,泊松比 0.3,抗拉强度 1000 MPa,屈服强度 800 MPa.轮边减速器壳体的材料为YL112,其抗拉强度 240 MPa,布氏硬度 85.

3.2 ATV工况

ATV的工况主要有：极限弯曲工况,极限扭转工况,制动工况,转弯工况,自由模态.本文以ATV车的极限扭转工况为例验证了拓扑和组合优化方法的可行性.扭转工况下车体的约束和载荷如下：

载荷：扭转工况下,来自地面的冲击力作用在 1轴的两个轮上,作用力大小相等方向相反.考虑到安全因子 f=3,则载荷大小 F=G×f=14000×3=42000 N.

约束：在扭转工况下,车体 4轴的两轮全约束.

3.3 ATV车身的拓扑和尺寸组合优化设计

车身在左右不相等的载荷作用下将产生扭转变形,假设把前后轴(轴距为 l)具有相同刚度的圆棒,即将车身的扭转刚性看成是简单圆棒的扭转刚性,其单位长度的扭转角为h,故车身的扭转刚度为[8]

式中：GJ为扭转刚度;L为轴距;T为扭矩;h为扭转角.

车体 1轴与 4轴之间的距离 L为 2016 mm;1轴两轮间的距离 l为 553 mm;支撑点作用力大小为 F=42000 N,方向相反;扭矩 T=42000×1.160=48720 N◦m.

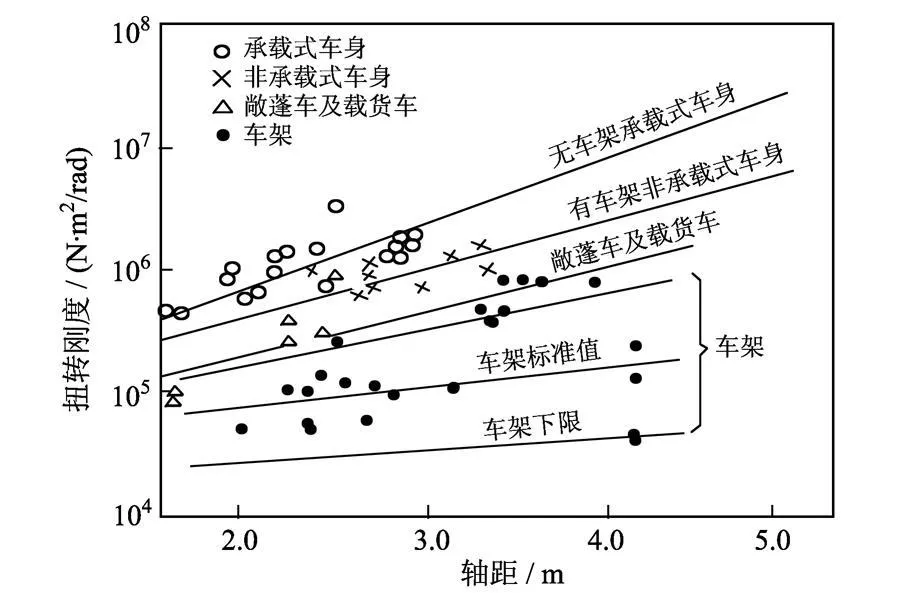
图2 山本图线Fig.2 Shanben graph

具体的优化设置如表 1所示,得到的优化结果如图 3所示.

表1 组合优化设置参数Tab.1 Combinatorial optimization parameters

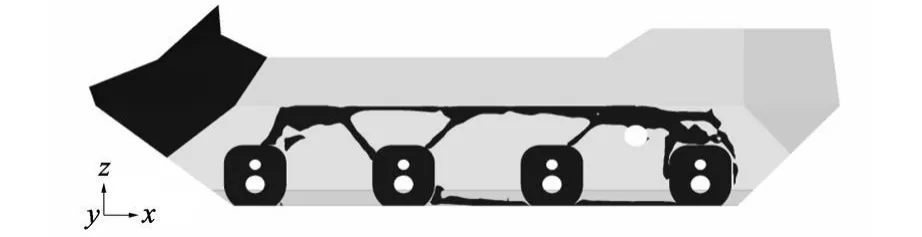
图3 车身拓扑和尺寸组合优化结构图Fig.3 Optimized structure of combinatorial optimization

3.4 优化结果分析

对比表 2中各项性能可知,组合优化方法得到的优化结构的最大应力比原车大了 4 M Pa,最大位移大了 0.99 mm,均都在结构的允许范围之内.组合优化方法得到的结构在质量上减少了105.5 kg,结构优化计算的收敛时间仅为 63 min.而且由得到的组合优化结构(图 3)可知,优化结构清晰、连续,整体无明显的材料堆积现象.

4 结 论

本文采用拓扑和尺寸组合优化方法对 ATV车身的结构进行了优化,在保证结构性能没有降低的情况下,结构的整体质量比原车减轻了105.5 kg.同时,得到的结构清晰、连续,整体无明显的材料堆积现象;该组合优化能够有效地减少车身在概念设计阶段的时间成本,提高了产品的市场竞争力.

[1]龙江启,兰凤崇,陈吉清.车身轻量化和钢铝一体化结构新技术的研究进展[J].机械工程学报,2008,44(6)：28-35.Long Jiangqi, Lan Fengchong, Chen Jiqing.Technology of lightweight and steel-aluminum hybrid structure car body[J].Chinese Journal of Mechanical Engineering,2008,44(6)：28-35.(in Chinese)

[2]许佩霞,蔡炳芳.基于 ANSYS的全地形车车架结构优化设计 [J].机械设计,2008,12(25)：56-58.Xu Peixia, CaiBingfang. Structuraloptimization design on frame of all topography vehicle based on ANSYS[J].Journal Ofmach Ine Design,2008,12(25)：56-58.(in Chinese)

[3]朱茂桃,蔡炳芳,束荣军,等.全地形车车架结构有限元分析与轻量化设计 [J].拖拉机与农用运输车,2008,35(3)：47-52.Zhu Maotao,Cai Bingfan,Shu Rongjun,et al.FEA and lightweight design for ATV frame structure[J].Tmctor& Farm Transporter,2008,35(3)：47-52.(in Chinese)

[4]王栋,张卫红,姜节胜.桁架结构形状与尺寸组合优化 [J].应用力学学报,2007,19(3)：72-76.Wang Dong, Zhang Weihong, Jiang Jiesheng.Combined shape and sizing optimization in truss design[J].Chinese Journal of Applied Mechanics,2007,19(3)：72-76.(in Chinese)

[5]Tang P S,Chang K H.Integration of topology and shape optimization for design of structural components[J].Struct.Multidisc.Optim.,2001,22：65-82.

[6]傅晓锦.拓扑与形状集成优化算法的关键技术研究[D].杭州：浙江工业大学,2008.

[7]Arora J S,Haug E J.Methods of design sensitivity analysis in structural optimization[J].AIAA Journal,1979,19(9)：970-974.

[8]乐玉汉.轿车车身设计[M].北京：高等教育出版社,2000：43-44.