Curves with Null Principal Normal Vector in 3－Dimensional Minkowski Space＊

2012-09-09HUANGRongpeiYUJunyan

吉首大学学报（自然科学版） 2012年3期

HUANG Rongpei，YU Junyan

（1.Department of Mathematics，East China Normal University，Shanghai 200241，China；2.Shanghai Science and Technology Management School，Shanghai 200433，China）

HUANG Rong－pei1，YU Jun－yan2

（1.Department of Mathematics，East China Normal University，Shanghai 200241，China；2.Shanghai Science and Technology Management School，Shanghai 200433，China）

The authors study the actions on spacelike curves with null principal normal vector in 3－dimensional Minkowski space.The Euler－Lagrange equation and two Killing vector fields are found.The authors integrate the Frenet equations by constructing cylindrical coordinates around the Killing field P.

spacelike curve；null principal normal；Killing field

1 Introduction

In recent years，many interesting works concerning Lagrangians describing geometric particle models have been published（ref.［1－2］）.The admissible Lagrangian density must depend on the curvature of curves due to the Poincaréand invariance requirements.We will study the actions on a small family of spacelike curves with null principal normal vector in 3－dimensional Minkowski space.

Let E31be a 3－dimensional Minkowski space with the Lorentzian inner product

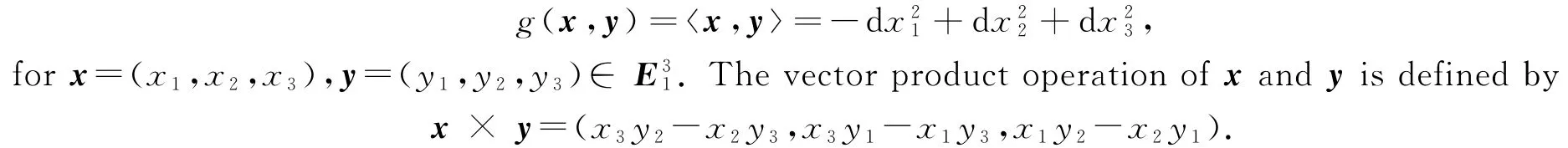
Since g is an indefinite metric，a vector v∈E31can have one of the three causal characteristics：it can be spacelike if g（v，v）＞0 or v＝0，timelike if g（v，v）＜0 and null（lightlike）if g（v，v）＝0 and v≠0.A curveγ＝γ（s）incan be locally spacelike，timelike or null，if all of its velocity vectorsγ′（s）are respectively spacelike，timelike or null.v is a unit vector if g（v，v）＝±1.Two vectors u，v are said to be orthogonal if g（u，v）＝0.

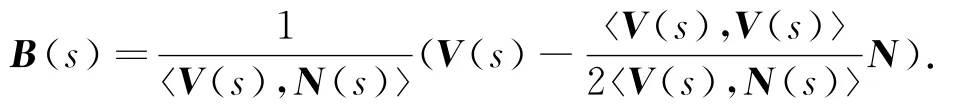
We call the frame｛γ（s）；T（s），N（s），B（s）｝a Frenet frame of the curveγat s.By a direct calculation，we obtain the Frenet formula of the curveγ.

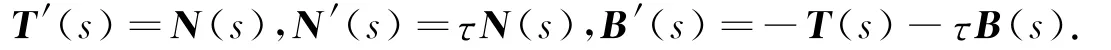
The vector product of the frame vectors T（s），N（s），B（s）are

The fundamental theorem for the curves with null principal normal vector tells us thatτdetermines completely the curve up to Lorentzian transformations.

2 Motion of the Curves with Null Principal Normal

In this section，we study the mechanical systems with Lagrangians depending arbitrarily on the curvatureτ（s）of the spacelike curves having null principal normal vector.The space of the variation curves of this model is the setΛof all spacelike curves having null principal normal vector fulfilling given first order boundary data to drop out the boundary terms which appear when computing the first variation of the curvature functionals.

The letterγwill also denote a variationγ＝γ（w，t）：（－ε，ε）×withγ（0，t）＝γ（t）such that every curveγw（t）＝γ（w，t）has null principal normal vectors.Associated with such a variation is the variation vector field W（t）＝（∂γ／∂w）（0，t）along the curveγ（t）.We will also write W（w，t）＝（∂γ／∂w）（w，t），T（w，t）＝（∂γ／∂t）（w，t），etc.，with the obvious meaning.Let s denote the arclength parameter，and we writeγ（w，s），τ（w，s），etc.，for the corresponding reparametrizations，l be the arclength of γ.We may assume t＝s be the arclength parameter ofγand then I＝［0，l］.By a direct computation，we have the following lemma.

Lemma 1 Using the above notation，we have the following formulas：

（ⅲ）［W，T］＝g T；

We consider the action F：Λ→R given by

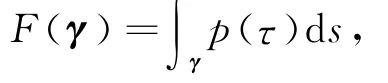
where p is a differentiable function.A curveγ∈Λwill be called a critical point of the action F if

for all variation of curvesγw∈Λofγ.

We use a standard argument involving some integrations by parts and obtain the first variation formula of the action F along the elementary fields spaceΛ.

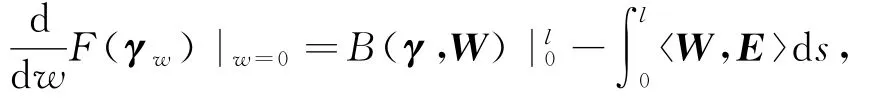
where

P＝（p′（τ）′－p′（τ）τ＋p（τ））T＋（f′（s）＋τf（s）－p′（τ））N＋（p′（τ）″－τp′（τ）′）B，and the boundary term reads

Then the Euler－Lagrange equation is

This is a third order ordinary differential equation ofτ.Once we solve it，we can choose a special function f.Equation（1）implies that along a critical point of the action F，P is a constant vector field.

3 Cylindrical Coordinate Expression of the Critical Point

In this section，we will use the Killing vector fields（ref.［3］）to construct a cylindrical coordinate to express the critical point of the action F.

A vector field V alongγwhich infinitesimally preserves the casual character of N，the arclength parameter and the curvature ofγis said to be a Killing vector field alongγ.

By lemma 1，Killing vector field alongγsatisfies the following equations：

The dimension of the solution space of the above equations is 6.It agrees with the dimension of Lorentz group of E31.Thus a Killing vector field alongγcan extends to a Killing field on E31.

Along the critical curve，the first variation formula reduces to

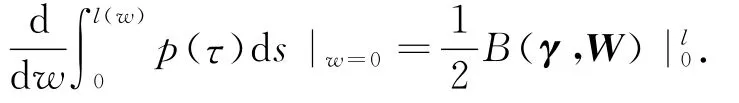
For a Killing field W，the variation of F（γ）is zero.This variation formula continues to hold when l is replaced with any intermediate value l′，0＜l′＜l.It follows that B（γ，W）is constant on［0，l］.The rotations of E31also leave F（γ）unchanged.A vector field on E31generates a one－parameter family of rotations when it is of the formγ×Z，where Z is a constant vector field.We obtain

is constant for any constant vector field Z.Therefore the vector field

is a constant vector field.It means that J is a translation followed by a rotation，and so it is a Killing vector field.This means that P and J are restrictions of Killing fields in flat space along critical curves.E－quation（2）implies

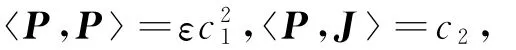
whereε＝±1 is the causal sign of P and c1，c2are constants.

By translating the origin and using the property of the vector product，the Killing field J can be written as

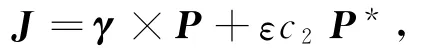
where P＊is a vector field with the same causal character as P and satisfying〈P，P＊〉＝ε.We divide it into two cases：P is nonnull or P is null.

（ⅰ）P is nonnull.Up to a Lorentz transformation，we can choose a cylindrical coordinate inwith P as the z－axis.When P is spacelike，it can be written as（r coshθ，r sinhθ，z）.When P is lightlike，it is（z，r cosθ，r sinθ）.The metric can be written as d s2＝εd z2－εd r2＋r2dθ2.At this time，and.From the expression，we have：

Theorem 1 Letγ∈Λbe the critical point of the action F，P a nonnull vector field.Thenγcan be expressed in cylindrical coordinates around P as

where

（ⅱ）P is null.Up to a Lorentz transformation，we can assume P＝a（1，1，0）andThen we choose the null cylindrical coordinates around P as，－εrθ）.The metric can be written as d s2＝2εd r d z＋r2dθ2.At this time，1））From the expression T（s）＝z′（s）∂＋r′（s）∂＋θ′（s）∂，we have：zrθ

Theorem 2 Letγ∈Λbe the critical point of the action F，P a null vector field.Thenγcan be expressed in null cylindrical coordinates around P as

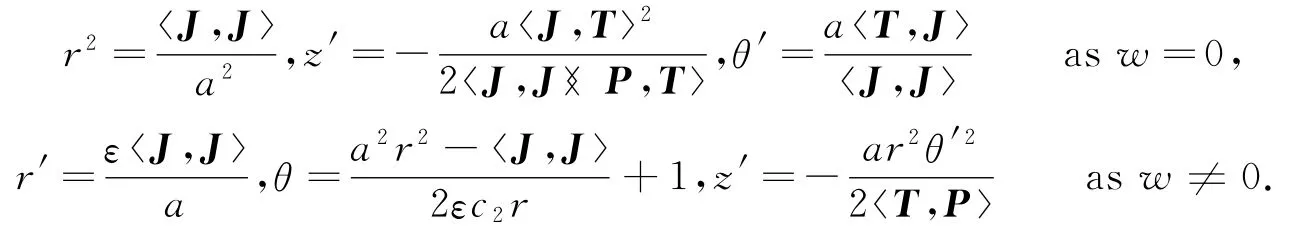
［1］ FERRANDEZ A GUERRERO，J JAVALOYES M，LUCAS P.Particle with Curvature and Torsion in Three－Dimensional Pseudo－Riemannian Space Forms［J］.Journal of Geometry and Physics，2006，56（9）：1 666－1 687.

［2］ HUANG Rong－pei，LIAO Cai－sheng.Geometrical Particle Models on 3D Lightlike Curves［J］.Modern Physics Letters，2006，21（40）：3 030－3 048.

［3］ LANGER J，SINGER P.Lagrangian Aspects of the Kirchhoff Elastic Rod［J］.SIAM Review，1996，38（4）：605－618.

3维闵可夫斯基空间中具有类光主法向量的曲线

黄荣培1，余俊燕2

（1.华东师范大学数学系，上海 200241；2.上海科技管理学校，上海 200433）

研究了3维闵可夫斯基空间中具有类光主法向量的类空曲线，求出了欧拉－拉格朗日方程和2个Killing向量场，通过建立围绕Killing向量场P的柱面坐标系解出了Frenet方程.

类空曲线；类光主法向；Killing场

O186

book=0,ebook=23

O186 Document code：A

10.3969／j.issn.1007－2985.2012.03.004

（责任编辑向阳洁）