矿用行星轮系的接触疲劳仿真分析

黄学文

(天地科技股份有限公司，北京100013)

式中，FH为齿轮的承担载荷;L为接触线的长度; ρΣ为啮合齿面上啮合点的综合曲率半径;E1和E2为齿轮材料的弹性模量;μ1和μ2为齿轮材料的泊松比。

矿用行星轮系的接触疲劳仿真分析

黄学文

(天地科技股份有限公司，北京100013)

对行星轮系接触疲劳的相关特性进行分析，建立了行星轮系的三维有限元模型，获取了定轴行星轮系的接触应力载荷谱和接触疲劳S－N曲线。利用ANSYS Workbench软件，以一组矿用行星轮系为实例进行接触疲劳仿真分析，得到了行星轮系的寿命和安全系数等相关参数。仿真结果表明:接触疲劳仿真分析为行星轮系的可靠性设计和结构优化提供了重要的保障。

行星轮系;接触疲劳;S－N曲线;安全系数

在所有的机械传动过程中，齿轮传动具有传动效率高、承载扭矩大、工作寿命长等特点，因而应用最广。接触疲劳破坏是齿轮失效的重要原因之一，齿轮的齿面处多容易发生点蚀、磨损和胶合等疲劳破坏现象，从而造成了齿轮的严重失效。卢金生［1］对齿轮渗氮层强度进行了深入研究，借助有限元仿真的方法，获取了正交切应力沿渗氮层深度方向上的分布情况，并且通过齿轮接触疲劳试验验证了齿轮渗氮层的可靠性;李贞子［2］利用疲劳接触试验机对齿轮进行接触疲劳试验，总结出不同材料和工艺条件下的齿轮接触疲劳强度极限。运用有限元方法对齿轮进行接触疲劳仿真分析具有很大的优势，不仅可以精确找到齿轮容易发生疲劳破坏的部位，而且大大提高了接触疲劳分析的效率。

本文以一组常用矿用行星轮系为例，建立了行星轮系的三维有限元模型，然后对其进行接触疲劳仿真分析。

1 行星轮系的接触疲劳特性

齿轮在高速传动的过程中，由于受到反复交变接触应力的直接作用，齿面接触部位往往产生接触疲劳。同一齿面的齿轮往往齿根先发生点蚀，然后才扩展到齿顶面，所以齿顶面比齿根面具有更高的接触疲劳强度。根据赫兹接触理论，齿面接触往往当做节圆处的两个圆柱体接触，在压力的作用下，由于接触表面发生局部变形，最大接触压力σH发生在接触带的各点上，形成宽度为2b的接触带。最大接触应力σH和接触带半宽b的求解如式 (1)和式 (2)所示［3］。

式中，FH为齿轮的承担载荷;L为接触线的长度; ρΣ为啮合齿面上啮合点的综合曲率半径;E1和E2为齿轮材料的弹性模量;μ1和μ2为齿轮材料的泊松比。

根据式 (1)可得，由于承担载荷FH、接触线长度L和综合曲率半径ρΣ，随着行星轮系啮合点位置的不同而不同，接触应力σH的大小也不同，因此，为了保证行星轮系疲劳仿真分析结果的准确性，必须对齿面接触部位进行精确地建模。

2 行星轮系三维有限元建模

2.1 创建渐开线齿廓

如图1所示，发生线沿着基圆作纯滚动，K为发生线上的任意一点，K点移动形成的轨迹便称为渐开线，根据渐开线齿廓的形成原理图，得到渐开线的极坐标参数方程式为［4］:

式中，rk为渐开线向径;rb为渐开线基圆半径;αk为渐开线在K点压力角;θk为渐开线AK段展角。

图1 渐开线的形成原理

2.2 模型的简化与网格划分

完成对渐开线齿廓的创建以后，通过镜像、拉伸等一些列命令形成单齿的实体模型［5］(图2)。在建立单齿的三维实体模型时，由于齿轮内部的应力对齿面接触部位的影响不是很大，因此对齿轮的内部进行简化处理，不建立轴孔和键槽。

图2 单齿的实体模型

如图3所示，为了便于网格的手工划分，将单齿实体平面划分为6部分，第1、第2部分为内部简化部分，第3、第4部分为齿根部分，第5、第6部分为齿面部分。齿面接触部位的网格划分类型和网格密度对接触疲劳仿真分析的结果准确性具有重要的影响，对单齿的实体模型采用映射划分和扫掠划分2种方法，这2种划分方法比较复杂，但是划分的网格形状规则，计算精度提高;同时对齿面第5部分和第6部分的网格进行加密处理，防止接触部位发生应力奇异，从而保证了仿真分析的准确性。为了尽可能使齿轮之间的接触符合实际情况，单齿网格划分选择Solid45实体单元类型，该单元类型在六面体的8个端点上各有1个组成节点，每个组成节点分别具有x，y和z 3个方向的平移自由度，2种单元具有屈服、应力强化、大变形和大应变等能力。划分后的单齿网格模型如图4。

图3 单齿划分

图4 单齿的网格模型

对单齿网格模型进行阵列便形成齿轮的整个有限元模型，如图5所示，选取某公司的一组矿用行星轮系为例，考虑到计算机的计算效率和存储空间的大小，太阳轮和行星轮接触处、齿圈和行星轮的接触处各选取5对轮齿建立接触疲劳仿真分析的有限元模型。

图5 行星轮系的有限元模型

3 行星轮系模型的约束和加载

3.1 接触对的建立

为模拟行星轮系齿轮之间相互接触情况，需建立对应的接触对。接触单元Contact174与配对的目标单元Target170作为行星轮系的接触对单元类型，行星轮系的非线性接触属于柔体与柔体间接触，在太阳轮和行星轮的啮合处，选用行星轮接触面为目标面，太阳轮接触面为接触面;在齿圈和行星轮的接触处，选用行星轮接触面为目标面，齿圈的接触面为接触面，建立的接触对如图6。

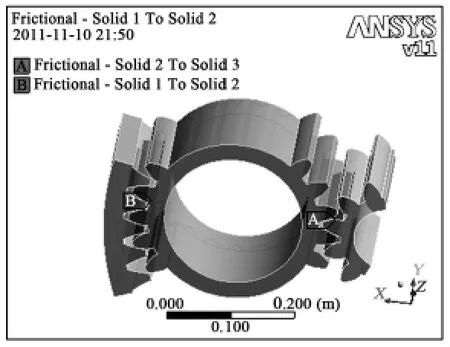
图6 行星轮系的接触对

接触对之间的摩擦力可以通过摩擦系数的设定直接进行定义，接触对之间采用罚函数法与拉格朗日法混合的广义拉格朗日法，这种方法不停地重复更新接触刚度，直到计算的穿透值小于允许值为止。广义的拉格朗日法的优点为对接触刚度系数不是很敏感，不易引起刚度矩阵的病态，能够更好地模拟仿真结果。

3.2 刚性区的建立与内齿圈的约束

对行星轮系有限元模型进行简化，建立刚性耦合区可以大大提高计算效率。将齿轮旋转中心与齿轮的内表面耦合在一起，使其旋转中心与齿轮内表面具有相同的自由度，从而形成刚性区［6］。对太阳轮和行星轮而言，以各自旋转中心与其齿轮的内表面建立耦合关系，从而形成太阳轮和行星轮的内部刚性区。对太阳轮和行星轮旋转中心进行自由度控制，使其只具有绕Z轴旋转方向的自由度，从而太阳轮和行星轮只具有绕Z轴旋转方向的自由度，即限制UX，UY，UZ，RX和RY五个方向的自由度，放开RZ方向的自由度。太阳轮和行星轮的刚性区如图7所示。内齿圈完全约束其自由度，即完全限制UX，UY，UZ，RX，RY和RZ六个方向的自由度，如图8所示。

图7 太阳轮和行星轮的刚性区

3.3 转矩的施加

图8 内齿圈的完全约束

如图9所示，在进行接触疲劳分析时，需要将转矩顺时针加载到太阳轮的旋转中心上，转矩将会通过刚性区传递到整个太阳轮上。为了使仿真结果收敛，转矩采用斜坡加载的方式，在1s的时间内转矩从零斜坡加载到最大值，如图10所示。

图9 转矩的施加

图10 转矩的施加

4 行星轮系载荷谱和S－N曲线的确定

行星轮系是一个重复旋转的过程，因此，齿面的接触应力是随时间发生变化。当靠近接触点时，从最小值0增大到最大值;当远离接触点时，又从最大值减少到最小值0。

齿轮在高速旋转的过程中，作用应力水平较低，弹性应变起主导作用，疲劳寿命较长，一般不会发生低周疲劳破坏。当在高周疲劳区时，由于齿面受交变接触应力的循环作用下，齿轮啮合的部位容易发生接触疲劳失效。

在恒幅作用下的疲劳寿命，可以直接利用S－N曲线进行接触疲劳寿命计算。根据式 (3)对不同的成活率可以采用P－S－N曲线［7］，不但得到在给定应力水平下失效循环次数N的分布数据，而且得到在给定的有限寿命下疲劳强度S的分布数据。

式中，NP是存活率为P时的接触疲劳寿命;S是接触应力，它对应于某一应力比的应力幅值或最大应力。ap和bp是与存活率有关的材料常数。

如图11和图12所示，以材料20Cr2Ni4A和42CrMo为例，假定疲劳分析曲线的存活率为99%，根据获得的平均应力数据与材料疲劳数据，分别得到齿面接触疲劳双对数形式的S－N曲线。

图11 20Cr2Ni4A的接触疲劳S－N曲线

图12 42CrMo的接触疲劳S－N曲线

5 疲劳分析的求解以及后处理

为了使接触疲劳仿真结果收敛，必须设定合适的载荷步数，打开自动时间载荷步选项，求解器选择PCG类型。对仿真结果进行后处理分析，图13和图14表明了定轴行星轮系在接触疲劳寿命的设计范围之内不会发生疲劳破坏。对齿面接触部位的安全系数情况进行具体研究，图15、图16和图17分别表明了太阳轮的接触疲劳安全系数处于3～3.5之间，行星轮接触安全系数处于3～3.5之间，齿圈接触安全系数处于2.5～3.5之间。

6 结论

本文的接触疲劳仿真分析是完全的无侧隙啮合的情况下进行分析的，而实际的行星轮系的传动过程中可能存在一定的间隙，因此分析结果与实际情况可能有微小的不同。

图13 接触疲劳寿命

图14 接触疲劳损伤

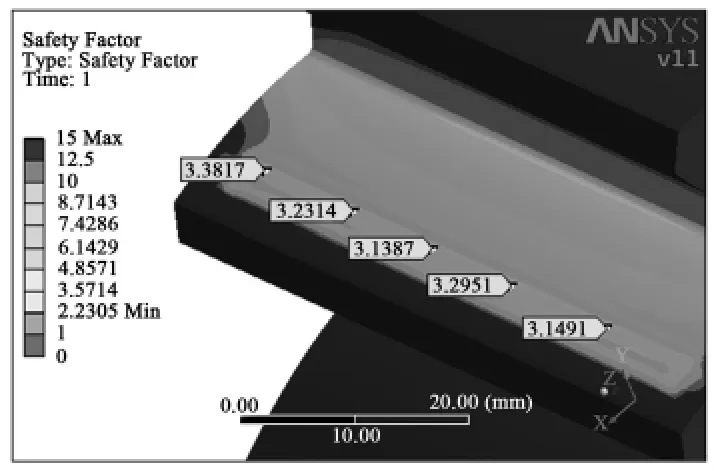
图15 太阳轮的安全系数

图16 行星轮的安全系数

图17 齿圈的安全系数

本文对行星轮系进行了接触疲劳仿真分析，合理评价了行星轮系的接触疲劳情况，得到了太阳轮、行星轮和内齿圈接触部位的具体安全系数，为行星轮系的设计优化奠定了重要的基础。

［1］卢金生.渗氮齿轮硬化层设计及接触疲劳性能研究［J］.金属热处理，2011，36(3):95－98.

［2］李贞子.材料和工艺对齿轮接触疲劳性能的影响［J］.汽车工艺与材料，2006，4(2):12－14.

［3］濮良贵.机械设计［M］.北京:高等教育出版社，2006.

［4］李华敏.齿轮结构设计与应用［M］.北京:机械工业出版社，2007.

［5］李学艺，李三帅，王 权，等.基于ANSYS的NWG型直齿行星轮系参数化建模［J］.机械传动，2011，35(1).

［6］李学艺，李三帅，曾庆良.基于动力学的矿用减速器渗碳齿轮强度研究［J］.煤炭学报，2011，36(7):1127－1231.

［7］陈传尧.疲劳与断裂［M］.武汉:华中科技大学出版社，2001.

［责任编辑:徐亚军］

Simulation Analysis of Contact Fatigue for Mine Planet Gears

HUANG Xue-wen

(Tiandi Science＆Technology Co.，Ltd.，Beijing 100013，China)

3-D finite element model of planet gears was set up and contact stress load spectrum of fixed-axial planet gears and S-N curve of contact fatigue was obtained by analyzing related characteristics of contact fatigue of planet gears.Applying ANSYS Workbench software to analyzing contact fatigue of a set of mine planet gears，life and safety coefficient of planet gears was obtained.Simulation result showed that contact fatigue simulation analysis provided guarantee for reliability design and structure optimization of planet gears.

planet gears;contact fatigue;S-N curve;safety coefficient

TH132.41

A

1006-6225(2012)04-0017-04

2012－04－27

中国博士后科学基金第二批特别资助项目 (200902286)

黄学文 (1972－)男，湖北武汉人，博士后，高级工程师，从事科研管理及煤机传动和再制造方面的研究。