水合物钻井液微观结构热传导分形模型研究

韩博，李承中，范勇，姜淼

(1．中水北方勘测设计研究有限责任公司，天津320222;2．福建省建筑科学研究院，福建福州350025; 3．中铁隧道勘测设计院有限公司，天津300133)

水合物钻井液微观结构热传导分形模型研究

韩博1，李承中1，范勇2，姜淼3

(1．中水北方勘测设计研究有限责任公司，天津320222;2．福建省建筑科学研究院，福建福州350025; 3．中铁隧道勘测设计院有限公司，天津300133)

在水合物勘探开发过程中，钻井液除常规作用外，还必须具有抑制水合物分解与再生成的作用。钻井液的这些宏观作用由其内部微观结构所决定，而水合物的分解和生成与介质的传热过程有关。由于钻井液微观结构与多孔介质相似，故其传热过程也相似。利用多孔介质的性质及其传热理论，系统分析了水合物钻井液微观结构与多孔介质的异同，探讨了水合物在钻井液中的分解特性。接着阐述了分形理论，对钻井液微观结构的传热分形模型进行了研究。最后得出钻井液中水合物分解的传热过程，建立了钻井液微观结构的一维热传导分形模型，并得出有效导热系数的分形表达式。

水合物钻井液微观结构热传导分形

Han Bo，Li Cheng－zhong，Fan Yong，Jiang Miao．A fractal model of heat conduction for the drilling fluid microstructures in hydrate formation［J］．Geology and Exploration，2012，48(4):0829－0834．

1 引言

在水合物地层钻进中，井壁附近水合物的分解和环空中水合物的分解与再形成，很可能会引起井壁失稳坍塌以及环空堵塞等复杂情况，从而影响钻井的顺利进行。

钻井液作为钻井过程的一个重要组成部分，其各组分所形成的微观结构在解决钻井问题中起着重要的作用，微观结构发生变化对其中水合物分解的传热过程产生重要的影响。当前国内外研究油气勘探和油气输送中水合物的形成和分解，主要是利用高压微差示扫描量热仪(DSC)对水合物抑制性评价和水基、油基钻井液以及输油管道中乳状液中水合物形成和分解的影响因素等进行研究，较少结合钻井液微观结构研究其对水合物形成和分解的影响。然而含聚合物的水基钻井液通常具有一定的微观结构，主要包括大分子聚合物等形成的网络骨架和中小分子量物质(水、盐类以及小分子聚合物等)组成的流动填充两部分。在一定条件下形成的这些网络骨架结构，既对溶液本体有支撑作用，又吸附和包裹着大量水分子，从而产生形变阻力，而含中、小分子物质(盐和抑制剂等)的水以填充形式存在于这些网络骨架结构中。这些微观骨架结构对钻井过程中进入其中的水合物分解的传热起着重要的作用。因此，有必要对钻井过程中钻井液微观结构对水合物分解的传热影响进行研究。

由于钻井液的微观网络骨架结构与一般多孔介质结构相似。而多孔介质的传热理论研究的比较多，并引进了分形理论。根据多孔介质的传热与分形理论对钻井液微观结构中的传热特性进行分析。因此，文中利用多孔介质的传热与分形理论，分析了含聚合物的无固相水基钻井液中天然气水合物的分解机理，最后建立钻井液微观结构中的热传导分形模型。

2 一般多孔介质的传热理论

一般多孔介质是由固体颗粒物质组成的骨架结构和骨架结构分隔成的大量密集的微小空隙所构成的物质(林瑞泰，1995)。概括来讲:

(1)一般多孔介质是固体颗粒胶结成的骨架结构，内部充满流体(液体、气体或气液混合物)，是一个由固相、液相、气相组成的统一结构体。

(2)多孔介质中固体骨架结构具有一定的孔隙度，并且有一些孔隙是相通的，流体在其中能够流动。

(3)整个多孔介质均有固体骨架结构分布，每个单元均可代替多孔介质。

2．1 多孔介质的传热过程

与单一均质物体中的热传递过程相比，多孔介质的传热过程要复杂得多(施明恒等，1994)，通常来讲，它主要有以下几部分:

(1)固体骨架之间的导热过程;

(2)多孔孔隙中流体的导热和对流换热过程; (3)固体骨架与流体之间的对流换热过程;

(4)固体骨架之间、固体骨架与孔隙中气体之间的辐射过程。一般来说，当多孔介质温度较低时，其辐射换热可以忽略不计。

2．2 钻井液微观结构与多孔介质结构的不同点

由于钻井液是由多组分物质组成的混合物，它的微观结构从某种程度上可以被看作是一种与添加纳米颗粒的悬浮液(王补宣，2009)相似的多孔结构，可以用同样的参数进行描述。钻井液的微观结构只不过是由高分子聚合物所形成的链状结构悬浮在钻井液中，其微观结构与一般的多孔介质有以下不同(张凌等，2011):

(1)最明显的不同就是钻井液的微观骨架结构是由高分子聚合物水化后所形成的网络骨架，而一般多孔介质是由固体胶结或支撑形成多孔结构。钻井液的网络骨架结构比多孔介质中的网络骨架结构尺寸相差悬殊，不在同一个数量级。

(2)钻井液网络骨架内部充填流体，处于动平衡状态，当钻井液流经钻头时，由于受到相对较大的剪切作用而发生拉伸、断裂等解构现象，流经环状空间中时可能会发生重构;而一般的多孔介质骨架结构通常处于稳定的固态，不会因流体的流动而发生明显变化。

(3)钻井液网络骨架结构强度较小，主要是由水化后的聚合物强度决定，并且受剪切作用影响明显;而一般多孔介质的网络骨架结构强度较高，决定于充填其中的物质。

此外，充填在钻井液网络骨架结构孔隙之中的流体也是钻井液的重要组成部分，其中水是重要的流动介质，它的存在状态为自由、半自由、不自由三种状态(田琴等，2003;谭帼馨等，2005)。水中所溶解的无机盐、高分子聚合物等对水合物分解的传热特性都起着重要的作用。

因此，当含水合物的岩屑进入具有一定微观结构的钻井液时，岩屑上的水合物就会被为这些微观结构所包裹，发生相互作用，而使其中水合物的分解与常见的室内或现场中的水合物分解特性存在不同。

3 钻井液微观结构中水合物分解特点分析

天然气水合物的分解涉及到固(水合物)、液(水)和气三相状态的转化。在水合物的分解过程中，影响较大的因素是温度、压力、水合物粒子表面积以及分解推动力等，并且水合物的分解是从表面逐层进行的。Jamaluddin A K M等(Jamaluddin A K M et al．，1989)认为水合物表面粗糙度随反应活化能的不同也会对分解速率产生不同的影响。Goel N等(Goel N et al．，2001)认为水合物的表面积和表面压差(水合物的平衡压力和水合物与气体的交界面的气相压力之差)是影响水合物分解速率的主要因素。而钻井液微观结构与含流体的多孔介质比较相似，但多孔介质体系中水合物分解的反应表面积很难确定。

在钻进过程中，钻井液的温度一般都高于0℃，进入钻井液中的水合物分解受到钻井液内部网络骨架和填充其中的流体的限制，其分解模型不同于由本征反应速率控制的水合物颗粒分解模型。而且，在水合物分解过程中，钻井液中各组分所形成的空间网架结构会将热量传递到水合物表面，水合物周围水中所含的盐类会因为浓度差进入分解生成的水而产生盐侵现象，盐离子的进入使水合物反应体系中溶液与冰之间的热传递阻力减小，有利于热量的传递。此外，加入盐类和乙二醇、增加初始温度(恒定外部压力)、降低外部压力、增加边界传热效率等都会加速水合物的分解。

钻井液各组分所组成的微观结构会对其中水合物的分解产生影响，但是不同体系中水合物反应的差别是由传热传质的差别造成的，因此，要了解和掌握钻进过程钻井液中水合物的分解动力学特性，就需要结合钻井液的微观结构变化对水合物分解传热特性加以探讨分析，进而对其相关模型加以完善。

4 钻井液微观结构中水合物分解的一维热传导分形模型

由于钻井液所形成的微观网络骨架结构极不规则，利用平均体积法进行研究不能正确的反应实际情况。因此，引入分形几何学理论来研究钻井液的微观网络骨架结构。

4．1 分形

分形是由美国著名的数学家Mandelbrot于1975年首先提出的(张济忠，1995)，用来研究自然界中存在的无序不规则的结构。由于分形可以描述自然界中存在的大量不规则结构，因此得到了世界各国科学家的关注，并且逐步形成了分形几何学理论体系(施明恒等，2001)。分形几何学理论能够解释非线性现象并证实任意分散结构的客观规律。分形理论直接从非线性复杂系统本身着手，认为空间维数可以不是整数，从而突破了传统欧氏几何理论的局限。

Katz A J等(KATZ A J et al．，1985)利用分形几何理论来分析多孔介质的内部几何结构。Wu J．S．和Yu B．M．(Wu J．S．et al．，2007)于2007年基于多孔介质的分形特征和毛细管的孔喉模型建立了一个通过多孔介质流动阻力的分形模型。Yu(Yu B．M．et al．，2008)于2008年做出了一个评论，并试图在分形多孔介质中的流动领域应用分形几何学理论技术总结该理论、方法、数学模型、研究成果和开放式问题。Wang B．X．等(Wang B．X．et al．，2003)基于纳米粒子群和它的径向分布的表述有效的中间近似值和分形理论，提出建立有效“纳米流体”热传导的分形模型。Shou D．H．等(Shou D．H．et al．，2010)在2010年对粘性渗透性通过纤维介质提出了一个差异分形模型，并且该无非量纲渗透性的模型表述了孔隙度和分形维数的函数。很多研究人员(Zhang L．Z．et al．，2008;Ono Y．et al．，2009;Cai J．et al．，2010)已经关注将分形几何学理论应用到不规则的多孔介质。

目前研究多孔介质传质传热的较多，王补宣、施明恒等(王补宣，1994;施明恒，2001)对多孔介质中传质传热进行了深入的理论分析与研究，并且建立了多孔介质中的传质传热模型。因此可将钻井液的微观结构看作多孔介质进行传热理论分析研究。

4．2 分形模型

对于不规则物体，其尺寸大小M(L)与长度L有关，通过文献(Feder J．，1988)中的相似定律: M(L)～LDF，其中DF是物体的分形维数，如果两个物体的分形维数相等，那么这两个物体是自相似的; M(L)可以是一条线的长度或者一个面的面积或者一个立方体的体积或者是一个物体的质量;L是长度尺度。孔隙的数量与孔隙半径有关，如参考文献(Yu B．M．et al．，2002)所示的相似定律:

式中:rc是孔隙半径;rmax是最大孔隙半径。二维空间1＜DF＜2，三维空间2＜DF＜3。孔隙的总数，从最小半径rmin到最大半径rmax，由方程(2)可得:

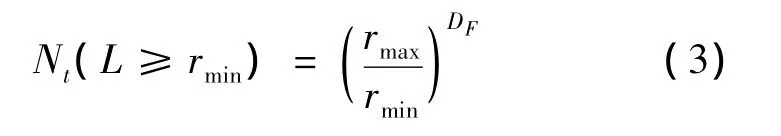
从方程(2)，还可得到:

式中:－dN＞0。方程(4)表示从半径rc到半径rc+drc的孔隙数量。方程(4)除以方程(3)可得:

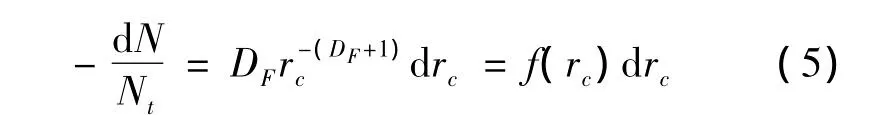
式中:f(rc)是孔隙分布的概率密度函数，其满足f(rc)≥0。方程(5)的积分形式是:

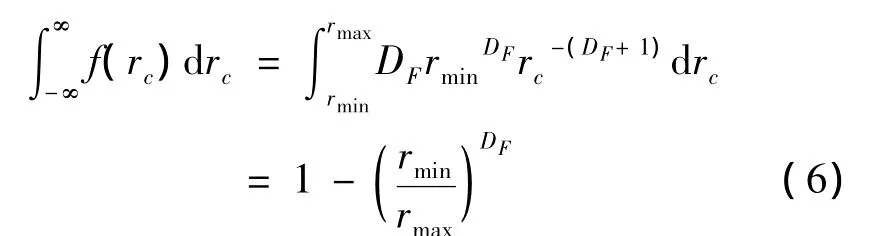
在概率论中，概率密度函数应该满足下面的关系:

方程(7)表明，若方程(6)成立，有且仅有:

方程(8)可看成是一个评判多孔介质是否具有分形理论特征的标准。通常在多孔介质中=0，方程(8)近似成立。

从rmin到rc的累积概率可由下式得到:

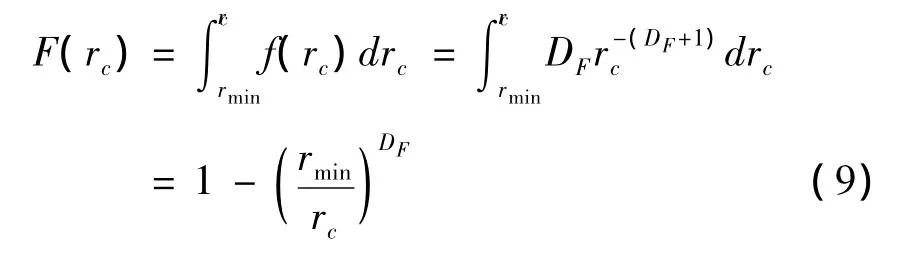
由方程(9)可知，当rc=rmin时，F(rc)=0，当rc=rmax，F(rc)≈1。

分形维数与多孔介质之间的关系如下表示:

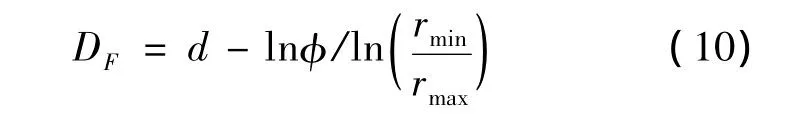
式中:d是欧几里德维数，在二维和三维空间分别是d=2和d=3。方程(10)表明当DF=d时，孔隙度φ=1，反之亦然。此式是合理的，当DF=d，空间完全被孔隙所占据并且所有孔隙形成一个统一的孔隙空间。当最小半径rmin与最大半径rmax已知时，分形维数DF是孔隙度φ的函数。孔隙度φ越大，分形维数DF越大。

4．3 钻井液微观结构导热的分形模型

前人对多孔介质中的传热过程一般都通过容积平均法计算固体骨架结构和流体所占份额，再进行导热计算，所得的结果与实际相差较大(张东辉，2003)。这几年来，由于分形的引入，可以将容积平均法的当量导热系数改变为分形导热系数来计算，可以比较真实的反应导热过程。

由于钻井液各组分形成的微观网络骨架结构比较复杂，热量在其中的传递也是一个复杂的过程。热量既可以能够大分子聚合物形成的网络骨架结构进行传导，也可以通过其中液体的流动与溶解在液体中的小分子物质的热传导以及与骨架结构的对流进行传热。如果网络骨架结构与其中的液体存在温差，那么它们之间还存在导热和对流。水合物分解的气体和水进入钻井液中也携带着热量。因此，钻井液内部热量的传递与其中的微观结构有着密切的关系。

为了便于分析，假设网络骨架结构与内部流体之间存在热平衡，钻井液中流体的热量传递可以看作通过钻井液多孔骨架结构中气相和液相混合物的当量传导进行。即:钻井液中的传热主要由微观骨架结构的导热、流体的导热以及这两者之间互相导热之和组成(不考虑对流和辐射传热)。如图1所示，整个钻井液微观结构中热量的传递可以简化为通过网络骨架结构与充填其中的流体组成整个热传导过程。热量的传递主要通过钻井液的导热系数进行定量分析。钻井液导热系数不同，环空温度也不同，因此监测钻井液导热系数对于环空钻井液温度的预测具有重要的作用。导热系数实质上反映了钻井液在径向和轴向上导热热阻的大小(文乾彬等，2008)。

如图1所示，整个体系的导热系数可由孔隙中流体的导热系数与网络骨架的导热系数组成。传热过程可等效抽象成如图2所示一维热传导过程。将传热过程假设为热量通过平行的分形曲线路径在微观骨架结构与其中的孔隙中流体进行传递。热量的计算公式为:Q=ktSgradT，式中:Q为热量;k为导热系数;S为热量传递横截面面积;t为时间;gradT为温度梯度。

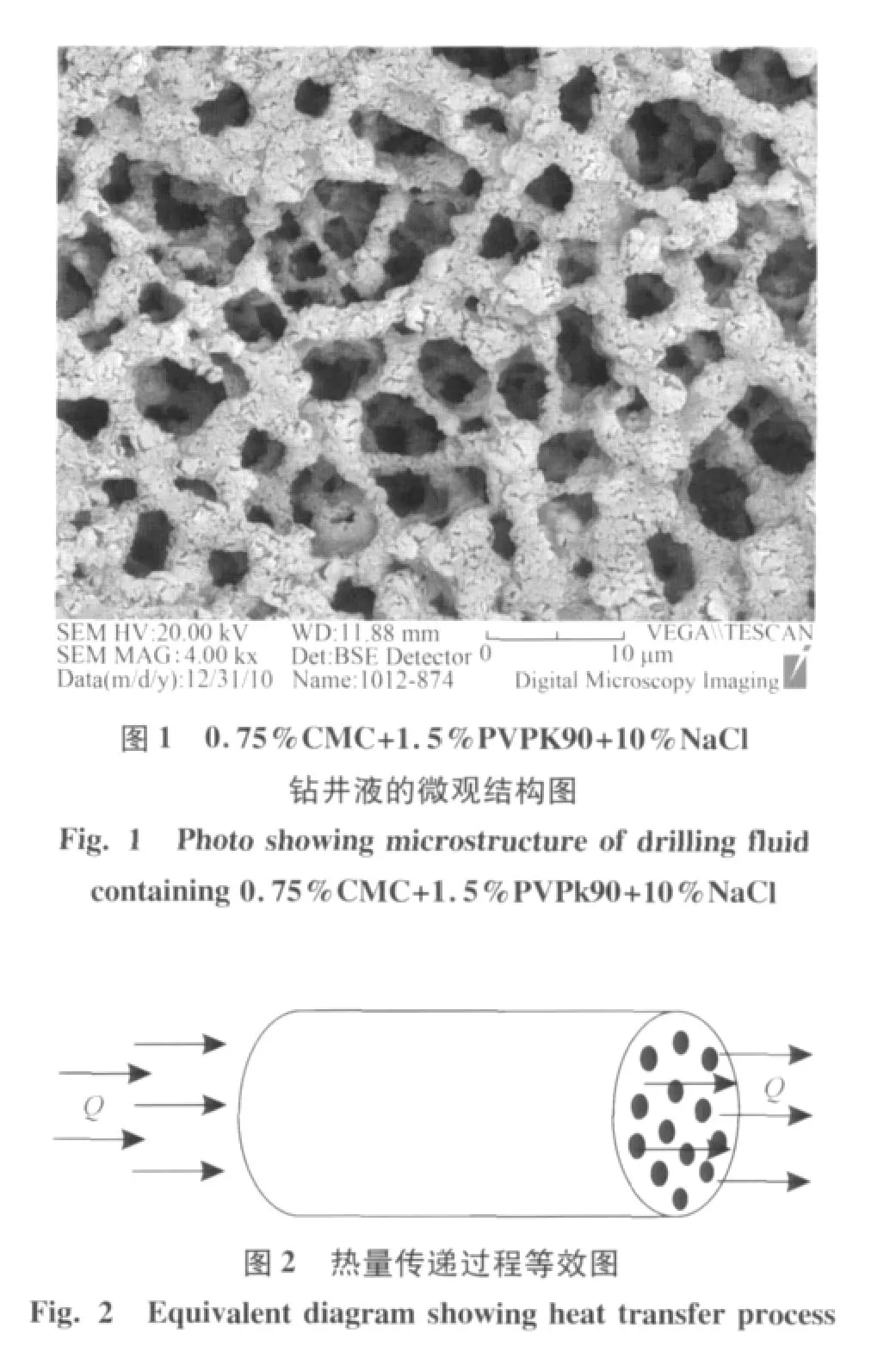
与多孔介质不同，图1所示钻井液中的固相为内部各组分形成的微观网络骨架结构，因此采用经验公式L(a)=L0a1－d(施明恒等，2002)来计算微观结构内部分形曲线的长度，式中:L(a)是曲线的长度，a为比例尺度，L0是曲线两端之间的直线距离，d是曲线的分形维数。

假设钻井液微观骨架形成的孔隙度为φ，则通过孔隙中流体传递的热量面积为φS，通过固体传递的热量面积为(1－φ)S，这里S是热量传递钻井液的横截面面积。钻井液的导热通道可简化成通过流体相和固相的并联通道。

钻井液微观结构的总导热热阻为:

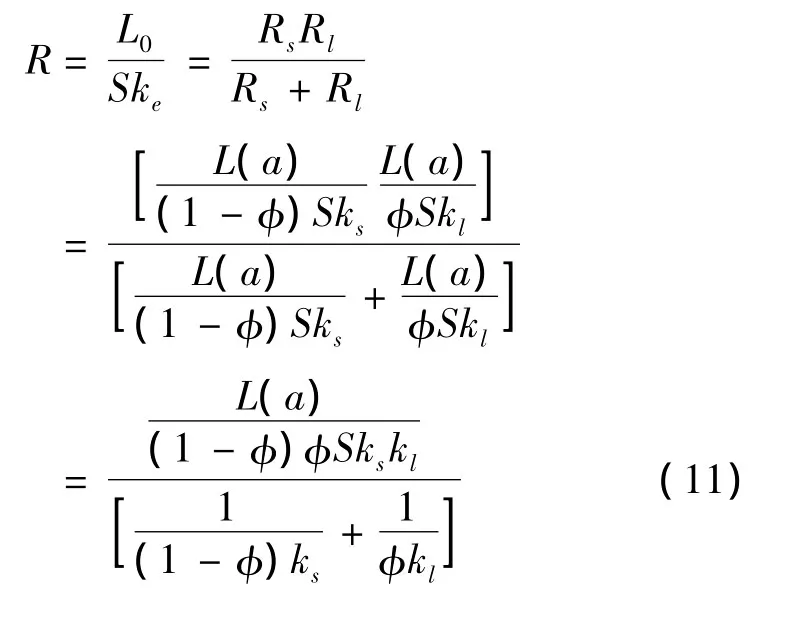
由此可得钻井液微观结构有效导热系数的分形表达式为:

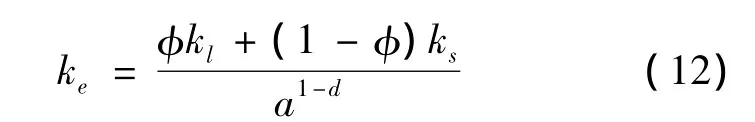
式中:kl、ks分别为钻井液微观结构中液相、固相的导热系数;ke为钻井液的有效导热系数。式(12)就是利用分形理论推出的与钻井液微观结构有关的有效导热系数关系式。分形维数与孔隙度的关系可利用式(10)进行计算。

分形模型的建立还可以根据SEM图片，经过CorelDRAW、autoCAD等软件转化为矢量图，再经过Heat transfer软件进行建模分析。

4．4 钻井液各组分与微观结构有效导热系数的关系

由式(12)可知，钻井液微观结构的有效导热系数与分形维数、孔隙度、比例系数以及各组分的导热系数有关。

钻井液微观结构中高分子聚合物网络骨架与其中充填的流体、流体中的离子等各自的导热系数不同，影响着钻井液的微观结构的有效导热系数。钻井液中聚合物起着导热作用，这部分用固相组分的导热系数表示，导热系数与微观结构的分形维数与孔隙度有关。它们组成的微观网络结构的孔隙度可通过微观图像，利用分形维数与孔隙度的关系式求得。充填于微观网络骨架结构中的水分子、无机盐分子等小分子物质一部分被吸附在聚合物表面，成为网络骨架结构的一部分;其余的以流体的形式在网络骨架结构中流动，可以通过热传导或对流导热的形式传递热量，流体中无机盐离子可促进热量的传递，这部分可用流体的导热系数来表示。

5 结论

(1)钻井过程中钻井液内含水合物岩屑的热量传递可以分为三个部分进行分析:①热量通过钻井液中网络骨架结构的热传导方式传递至水合物岩屑表面;②热量通过充填于钻井液网络骨架结构孔隙中的自由水、盐类小分子以及其它中小分子等流体以对流传热的方式传至水合物岩屑表面;③热量从水合物岩屑表面以热传导的方式向内传递。微观结构的导热系数决定着传热速率。

(2)根据多孔介质的分形理论，可以将钻井液微观结构的孔隙度与分形维数建立联系，DF=d－根据多孔介质的分形传热理论，将钻井液微观结构简化为一维热传导模型，推导出钻井液微观结构有效导热系数的关系式:ke=，影响有效导热系数的因素有微观结构的孔隙度、分形维数、导热系数等。

Katz A J，Thompson A H．1985．Fractal sandstone pores:Implications for conductivity and pore formation［J］．Phys Rev Lett，54:1325－1328．

Feder J．．1988．Fractals［M］．New York:Plenum Press:1－199

Jamaluddin A K M，Kalogerakis N．1989．Modeling of Decomposition of A Synthetic Core of Methane Gas Hydrate by Coupling Intrinsic Kinetics with Heat Transfer Rates［J］．Phys．Chem．，67(6):948–954

Shi Ming－heng，Yu Wei－ping，Wang Bu－xuan．1994．On the heat and mass transfer in porous media［J］．Journal of Southeast University，24(11):1－7(in Chinese with English abstract)

Wang Bu－xuan．1994．Convective heat and mass transfer in porous media［J］．Journal of Xi＇an Jiao Tong University，28(5):51－56(in Chinese with English abstract)

Lin Rui－tai．1995．Introduction to heat and mass transfer in porous medium［M］．Beijing:Science Press:1－348(in Chinese)

Zhang Ji－zhong．1995．Fractal［M］．Beijing:Tsinghua University press: 1－413(in Chinese)

Goel N，Wiggins M．2001．Analytical modeling of gas recovery from in situ hydrates dissociation［J］．Journal of Petroleum Science and Engineering，29:115－127

Shi Ming－heng，Chen Yong－ping．2001．The fractal theory of Heat and mass transfer in porous material［J］．Journal of Nanjing Normal University(Engineering and Technology Edition)，1(1):6－12(in Chinese with English abstract)

Yu B．M．，Cheng P．．2002．A fractal permeability model for bi－dispersed porous media［J］．Int．J．Heat Mass Transfer，45:2983–2993

Wang B．X．，Zhou L．P．，Peng X．F．．2003．A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles［J］．Int．J．Heat Mass Transfer，46:2665–2672

Zhang Dong－hui．2003．Diffusion，percolation and heat conduction in fractal porous media［D］．Nanjing:Southeast University:1－131(in Chinese)

Tian Qin，Zhao Xi－an，Tang Xiao－zhen，Zhang Yun－xiang．2003．Thermal analysis of the effect of hydrophobic microdomains on the water state of 2－(N－ethylperfluorooctaneus－lfoamido)ethyl methacrylate modified gels［J］．Acta Polymerica Sinica，1(2):180－185(in Chinese with English abstract)

Tan Guo－xin，Cui Ying－de，Yi Guo－bin，Zhou Jia－hua．2005．Influence of different states of water in hydrogels on tensile properties［J］．Journal of chemical industry and engineering，56(10):2019－2023(in Chinese with English abstract)

Wu J．S．，Yu B．M．．2007．A fractal resistance model for flow through porous media［J］．Int．J．Heat Mass Transfer，50:3925–3932

Yu B．M．2008．Analysis of flow in fractal porous media［J］．Appl．Mech．Rev，61:050801:1－19

Zhang L．Z．2008．A fractal model for gas permeation through porous membranes［J］．Int．J．Heat Mass Transfer，51(21－22):5288－5295

Wen Qian－bin，Liang Da－chuan，Ren Mao，Deng Sheng－hui．2008．Laboratory study on drilling fluid heat conductivity［J］．Petroleum drilling techniques，36(1):30－32(in Chinese with English abstract)

Ono Y．，Mayama H．，Furo I．，Sagidullin A．，Matsushima K．，Ura H．，Uchiyama T．，Tsujii K．2009．Characterization and structural investigation of fractal porous－silica over an extremely wide scale range of pore size［J］．J．Colloid Interf．Sci，336:215－225

Wang Bu－xuan．2009．Effect of particles clustering on the thermal properties and thermal processes of dilute nanofluids［J］．Chinese Journal of Mechanical Engineering，45(3):1－4(in Chinese with English abstract)

Shou D．H．，Fan J．T．，Ding F．．2010．A difference－fractal model for the permeability of fibrous porous media［J］．Phys．Lett，A 374:1201－1204

Cai J．，Huai X．L．．2010．Study on fluid–solid coupling heat transfer in fractal porous medium by lattice Boltzmann method［J］．Appl．Therm．Eng，30:715－723

Zhang Ling，Jiang Guo－sheng，Ning Fu－long，Han Bo，Dou Bin，Wu Xiang．2011．Discuss on effect of drilling fluid microstructures on heat and mass transfer characteristics of hydrate disassociation．［C］//seepage mechanics and engineering innovation and practice of the eleventh mechanics of seepage，annual meeting:Chongqing Chongqing University Press:206－211(in Chinese with English abstract)

［附中文参考文献］

施明恒，虞维平，王补宣．1994．多孔介质传热传质研究的现状和展望［J］．东南大学学报，24(11):1－7

王补宣．1994．多孔介质中的对流传热传质［J］．西安交通大学学报，28(5):51－56

林瑞泰．1995．多孔介质传热传质引论［M］．北京:科学出版社:1－348

张济忠．1995．分形［M］．北京:清华大学出版社:1－413

施明恒，陈永平．2001．多孔介质传热传质分形理论初析［J］．南京师大学报(工程技术版)，1(1):6－12

施明恒，樊荟．2002．多孔介质导热的分形模型［J］．热科学与热技术，1(1):28－31

张东辉．2003．多孔介质扩散、导热、渗流分形模型的研究［D］．东南大学:1－131

田琴，赵喜安，唐小真，章云祥．2003．热分析技术研究疏水缔合微区对含氟丙烯酸酯共聚物凝胶中水状态的影响［J］．高分子学报，1(2):180－185

谭帼馨，崔英德，易国斌，周家华．2005．水在凝胶中的存在状态及其对凝胶力学性能的影响［J］．化工学报，56(10):2019－2023

文乾彬，梁大川，任茂，邓生辉．2008．钻井液导热系数室内研究［J］．石油钻探技术，36(1):30－32

王补宣．2009．颗粒团聚对低浓度纳米流体热性质和热过程的影响［J］．机械工程学报，45(3):1－4

张凌，蒋国盛，宁伏龙，韩博，窦斌，吴翔．2011．钻井液微观结构对水合物分解传热传质特性的影响探讨［C］//渗流力学与工程的创新与实践，第十一届渗流力学年会，重庆:重庆大学出版社:206－211

A Fractal Model of Heat Conduction for the Drilling Fluid Microstructure in Hydrate Formation

HAN Bo1，LIN Chong－zhong1，FAN Yong2，JIANG Miao3
(1．China Water BEIFANG Investigation，Design＆Research Co．，Ltd，Tianjin320222; 2．FUJIAN academy of building research，Fuzhou，Fujian350025; 3．China Railway Tunnel Survey＆Design Institute Co．，Ltd，Tianjin300133)

In the process of the exploration and development of natural gas hydrate，drilling fluid should have the function of restraining the disassociation and regeneration of hydrate，besides the conventional functions．The macro－functions of drilling fluid are decided by its inner structure，and the disassociation and regeneration of hydrate are related to the heat transfer course of the media．As the microstructures of drilling fluid are similar to porous media，their heat transfer process is also similar．Using the heat transfer properties and theory of porous media，this paper analyzed the similarities and differences between drilling fluid and porous media，discussed the disassociation properties of hydrate in the drilling fluid，and studied the heat conduction fractal model for the drilling fluid microstructure．In conclusion，we obtained the heat conduction process of hydrate disassociation，established a one－dimensional heat conduction fractal model of drilling fluid microstructures，and got the fractal expression of effective coefficient for heat conduction．

hydrate，microstructure of drilling fluid，heat conduction，fractal

book=7,ebook=267

TK124

A

0495－5331(2012)04－0829－6

2011－11－17;

2012－02－08;［责任编辑］郝情情。

韩博(1984年—)，男，2011年毕业于中国地质大学(武汉)，获硕士学位，助理工程师，现从事水利水电地质勘察工作。E-mail:hanbo1984@126．com。