分形在岩性分类及蚀变信息提取中的应用

郑桂香，池天河，蔺启忠

(1.中国科学院遥感应用研究所，北京 100101;2.中国科学院对地观测与数字地球科学中心，北京 100086;3.中国科学院研究生院，北京 100049)

分形在岩性分类及蚀变信息提取中的应用

郑桂香1，3，池天河1，蔺启忠2

(1.中国科学院遥感应用研究所，北京 100101;2.中国科学院对地观测与数字地球科学中心，北京 100086;3.中国科学院研究生院，北京 100049)

为了推进多重分形思想在遥感地质找矿领域的应用，以新疆西准噶尔地区为实验区，通过分析该区的成矿特点与遥感影像特征，构建分形维数谱，并将其与图像光谱特征相结合进行岩性分类与含黄铁矿矿化蚀变信息提取，在现有矿点统计资料与专家经验知识的支撑下，确定找矿靶区。实践证明，基于遥感图像的分形理论并结合图像的光谱特征，建立相应的找矿模型和找矿标志，能更好地为区域矿产勘查提供决策支持。

分形;遥感找矿;岩性分类;蚀变信息提取;分形维数谱

0 引言

在遥感地质找矿领域，分形理论主要应用于图像蚀变信息提取、信息融合、辅助图像岩性分类以及模拟图像等方面［1－2］。Peleg 等人提出的双毯法［3］主要用于识别图像中目标与背景信息;舒宁采用分形方法进行了单波段图像的分维估计与多波段图像的纹理分析［4］。近年来，很多研究都将分形纹理信息引入到遥感图像分类中，用以区别不同的岩性单元:Chica［5］等结合西班牙地区TM图像的纹理信息，成功地提取了第四系岩层单元;Dong等［6］将光谱信息和分形纹理信息相结合，利用TM，SIR－C以及Radarsat数据提取了加利福尼亚和亚利桑那相临地区的岩性单元。本文将根据多重分形理论及光谱概念构建分形维数谱，通过对研究区不同岩性及地物分维谱特征的分析，提取岩性类别及蚀变信息，划定区域找矿靶区，为区域矿产勘查提供技术支持。

1 研究区与数据源

1.1 研究区概况

研究区(图1)位于新疆维吾尔自治区西准噶尔山东南缘与准噶尔盆地西缘的交接地带。区内植被覆盖度低，出露地层以上古生界为主，中生界次之，新生界仅在山麓地带及河谷中有零星分布。主要岩性包括太勒古拉组、希贝库拉斯组及包古图组的凝灰质粉砂岩、凝灰质砂岩、层凝灰岩及各侵入岩体中的花岗闪长岩、斜长花岗岩、花岗岩、钾长花岗岩以及第四系洪积、冲积层等。在南部及西部，分布有中、酸、基性脉岩，水晶矿、脉金矿分别与伟晶岩脉及石英脉有直接的成因联系，围岩蚀变发育地段(特别是黄铁矿化、毒砂化发育的地段)是找矿的重要位置［7］。

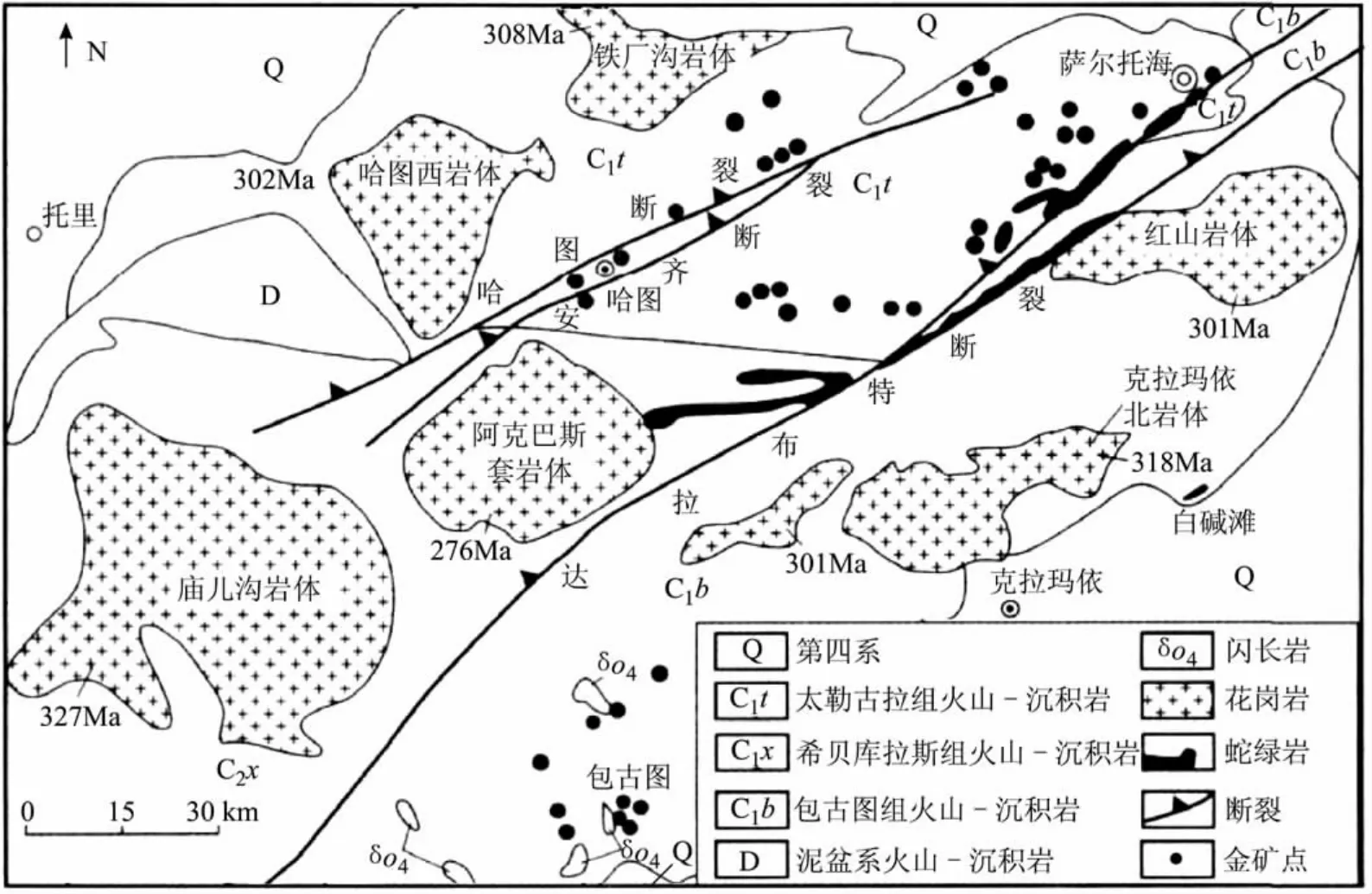
图1 研究区位置(据安芳［8］，2007)Fig.1 Position of study area(Modified after AN Fang)［8］

1.2 数据源

采用的遥感数据是2000年6月27日成像的ETM数据，其图像覆盖了整个研究区，图像质量良好。收集到的全国1︰20万数字地质图及矿产图资料时间跨度从50年代中期到20年代初期，主要格式为Coverage，分为地理、地质和图饰3大类图层。此外还有野外采集的光谱点经纬度数据、矿产统计资料数据以及专家判断和预测的相关资料等。

2 分形理论与方法

2.1 分形理论简述

分形理论由美国科学家 Mandelbrot［9］于20世纪70年代中期创立，是描述不规则几何形态的有效工具。地质现象的空间展布均具有分形结构特征，矿床是地壳物质自相似的突出实例［10］。李长江等［11］对萤石、金、银、铅锌和铜矿床进行了储量－数量的分形分布研究，通过建立分形成矿富集模型探讨矿床储量预测的分形原理和方法，将分形与地质统计学相结合进行矿石品位和储量计算。在地质构造方面，King［12］等人揭示了断裂具有分形分布特点。国内许多学者分别针对川滇［13］、柴达木盆地［14］、广西［15］、贵东［16］、高龙金矿区［17］、德兴铜矿田［18］、霍州矿区［19］以及东天山［20］等地的多处矿点与线性构造的分维特征进行过研究，通过分析分维值的异常与线性构造的关系，建立了找矿模型，圈定了找矿靶区。

Mandelbrot［9］指出，分形具有 3个要素:形状、机遇和维数。分形具有支离破碎、参差不齐的不规则形状;机遇是描述对象的差异性;维数则是用分数的形式来定量描述客观事物的“非规则”程度。分形维数是判断2个分形体是否一致的重要度量标准。在遥感图像的分形特征分析中，可将遥感图像的灰度图视为三维表面，像素的灰度值就是对应位置的高度，图像灰度的变化情况将反映在该表面的崎岖程度上。使用不同尺度去量测该表面，得到的维数就是分形维数。常见的遥感图像分形模型有Peleg的双毯法［4］、Pentland基于分数布朗运动模型提出的频谱法［10］以及Voss和Keller提出的求盒子中像素概率的分形盒模型和Chaudhuri提出的差分盒模型［21］。本文根据遥感图像的特点，采用Peleg的双毯法来计算分维值。

2.2 Peleg双毯法

Peleg在分形布朗随机模型的基础上，基于图像表面的灰度信息创立了“双毯法”。该方法将图像视为一座山丘，其高度为图像的灰度值，在距图像表面为r的两侧形成厚度2r的“毯子”。对于不同的r，“毯子”的面积可以重复如下计算。

设f(i，j)代表灰度值函数;u0，b0分别代表“毯子”上下表面的初始灰度值。令

则上下两张“毯子”分别沿

的方法生长。式中:r为尺度(r=1，2，…，n);ur，br分别代表在尺度r情况下“毯子”上、下表面的灰度值;d(i，j，m，n)代表(i，j)与(m，n)之间的距离。“毯子”的表面积为

由于分形表面积符合关系式A(r)≈k·r2－D，对等式两边同时取对数，则

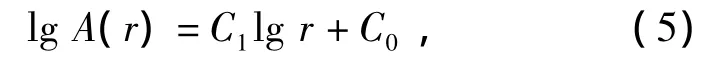
式中:C0为常数;C1为拟合直线的斜率。由此可以得到分形维数D=2－C1。

从理论上来讲，分形具有尺度不变性，即在所有尺度均满足自相似性，但实际图像仅在小尺度范围内呈分形特征，因为A(r)≈k·r2－D只是近似公式，lg r与lg A(r)并不是严格的线性关系，随尺度的变化，分维值也会发生变化，但最终会趋于恒定。

2.3 分维谱分析

为了更好地进行遥感图像岩性分类和提取蚀变信息，这里依据多重分形理论将多光谱或高光谱概念引入分形维数谱(简称分维谱)，即在特定分形尺度下，分维值随波段变化形成的特征谱线或者是特定波段图像下分维值随尺度变化的特征谱线，本文通过建立不同波段的分维谱进行图像分类与蚀变信息提取。

根据研究区地表覆盖特征提取出的植被、花岗闪长岩、超基性岩等地物和岩性的分维谱如图2所示。

图2 ETM1分维值随尺度变化图Fig.2 Fractal change as scale of ETM1

理论上而言，不同地物对应的分维值是唯一的，该值可用来标定目标物的不规则变化情况。但是，由于图像中混合像元的存在，随着尺度的变化，其分维值变化曲线渐趋平缓。从图2可知，当r=10，20时，分维对图像的依赖性很大，分维值变化异常剧烈，与灰度信息的变化成正相关关系，谱形变化曲线与光谱反射率变化曲线类似;当尺度大于20时，分维值受灰度变化的影响很小;当尺度为100时，分维值已趋稳定。因此，综合考虑计算机的运行效率，尺度越大，双毯迭代的次数越多，运行时间就越长。本文以20作为研究区的最佳尺度。此外，考虑到时间复杂度和图像的局部细节及边缘效应，采用5像元×5像元的滑动窗口来计算分维值，该窗口能较好地保留图像的局部特征。

由图3可知，当尺度r=10，20情况下，植被、地层、岩性之间的分维谱差异较大，植被分维谱呈现出与光谱相似的变化特征。不同地层、岩性谱形相似，但具有不同的分维值。钾质花岗岩和花岗闪长岩的分维值明显高于其他地层、岩性的分维值。同时地层岩性分维值存在这样的变化趋势:古生界＜中生界＜新生界，地层岩性＜花岗岩。

分维值是不同地球化学条件的反应:古老地层的活跃性不如新地层;侵入活动贯穿于各地层之间，比较活跃;同一岩层，不同的起源或者不同矿化作用的矿物具有不同的分维值［22］。

在本研究中，钾质花岗岩和花岗闪长岩的分维值大;古生代地层中的岩性主要为凝灰岩、凝灰质粉砂岩、层凝灰岩等，分维谱形基本类似。

图3 岩性分形特征谱Fig.3 Fractal spectra of lithology

3 方法应用及分析

3.1 岩性分类

从研究区中选取大小为443像元×443像元的典型区域作为实验区(图4(a))，利用Peleg双毯法对图像进行分形纹理提取(图4(b))，对比分析灰度信息和分形纹理信息，采用最大似然法进行图像分类。结果表明:与传统的基于灰度信息的分割方法(图4(c))相比较，有分形纹理特征参与的图像分类(图4(d))噪声小，细节信息多，精度上有明显提高，总体精度由76.81%提高到83.12%，Kappa系数由0.69提高到0.77。然而，两种分类均因白色河滩区域反射率比较高而分类精度不高。花岗闪长岩分布区也因存在此现象而产生一定的误分。此外，在分形纹理计算过程中产生了空值，导致部分区域没有参与分类。如何有效地改善这类缺陷是今后研究的重点。对比实验区地质图4(e)可以得出，有分形纹理参与的岩性分类结果较好地反映了实验区地层岩性的分布情况。

图4 实验区域效果图Fig.4 Result maps of study area

3.2 蚀变信息提取

由于多光谱数据波段数量少，基于谱形的蚀变信息提取方法往往达不到期望的效果。分维谱是根据多重分形理论，依据不同尺度对应的分维数或者不同成像条件建立起来的［23－24］，可弥补多光谱波段不足的缺点。统计资料表明，研究区的主要蚀变类型为黄铁矿化和毒砂化，野外观察表明，黄铁矿化在地表分布较多，而毒砂化很少。因此，本文在光谱的基础上加入分维谱，根据其生成原理的相似性和差异性，利用光谱角匹配法提取研究区蚀变异常信息。

通过遴选野外采集的62个含黄铁矿化蚀变样本，剔除了2个不理想的样本。依据其余的60个蚀变样本信息，从分维图像和反射率图像上提取出该蚀变样本的分维谱及光谱曲线，如图5－1(a)，(b)所示。并对样本数据进行标准化处理，得到含黄铁矿蚀变信息岩层的标准分维谱与标准光谱，如图5－2(c)，(d)所示。

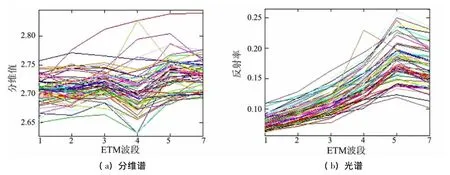
图5－1 黄铁矿蚀变样本谱形Fig.5 －1 Pyrite alteration sample spectrum

图5－2 黄铁矿蚀变样本谱形Fig.5 －2 Pyrite alteration sample spectrum

从图5可以看出，含黄铁矿化蚀变岩性的分维谱与光谱特征差异明显，具体体现在:

1)分维谱各样本的谱形整体呈一定规律，但样本间谱值波动范围较光谱值大，主要原因在于分维值的计算除考虑当前像元的灰度信息外，还综合考虑了与邻近像元的复杂关系。

2)从ETM1至ETM3，分维值和光谱反射率整体呈上升趋势，但分维值受地表覆盖情况的影响明显，特别体现在ETM4波段。这是因为，在该波段范围内，同一地层中相邻岩性对太阳光的吸收和反射相差不大，邻近像元灰度值相近，双毯的“毯”几乎无起伏，分维值较小;而该波段内光谱反射率较前几个波段差异不大，因此反射率整体呈递增趋势。

根据蚀变样本的标准分维谱与标准光谱曲线，采用光谱角匹配法提取出的研究区黄铁矿化蚀变信息如图6所示。

图6 研究区蚀变信息提取Fig.6 Alteration information extraction of study area

实验结果表明，黄铁矿化蚀变沿构造线集中分布于小岩体及其围岩接触带上。结合图4可知，希贝库拉斯组和包古图组地层的凝灰质砂岩和混砂岩中含大量的矿化信息，在包古图Ⅰ号、Ⅱ号、Ⅴ号岩体及其附近，蚀变信息分布集中。该区域矿点统计资料也显示，这些岩体附近矿化现象明显。图6上用黄色线圈定的找矿靶区是综合考虑了光谱与分维谱信息的结果;紫色线圈定的区域是仅考虑光谱信息提取出的蚀变异常，与用蓝色线(依据分维谱信息与专家知识)圈定的叠合区域一并视为次级找矿靶区。依据以上分析可知，分维值从一定程度上体现了成矿元素的活化及成矿流体的运移、聚集以及矿床的形成，与蚀变矿物谱形越相近的区域，对应蚀变矿化的概率就越高。克拉玛依北部岩体西侧图像特征满足上述条件，研究资料显示，在此区域已经发现了黄铁矿点及金矿点。

4 结论

本文结合新疆西准噶尔地区区域成矿特点和遥感图像特征，利用数学分形方法建立了岩性分类与蚀变信息提取的方法体系。分形维数是不同地球化学条件的反应，将分维谱参与岩性分类，可弥补多光谱波段不足的缺点，提高岩性分类精度。利用含黄铁矿化蚀变岩性的分维谱并结合光谱特征提取蚀变信息，能有效确定找矿靶区，为区域矿产勘查提供决策支持。

需要说明的是，本文仅考虑了岩性的分维特征，对矿床点的空间分布、密度及储量缺乏分析。如何获得该方面更多的数据，并结合构造、岩性分形来确定找矿靶区，是今后进一步研究的重点。

［1］何国金，薛重生.遥感地质学中若干问题的分形探讨［J］.国土资源遥感，1993(3):46－55.

［2］孙家柄，刘继琳，李 军.多源遥感影像融合［J］.遥感学报，1998，2(1):47 －50.

［3］Peleg S，Naor J，Hartley R，et al.Multiple Resolution Texture Analysis and Classification［J］.IEEE Trans PAMI，1984:6(4):518 －523.

［4］舒 宁.卫星遥感影像纹理分析与分形分维方法［J］.武汉测绘科技大学学报，1998，23(4):370 －373.

［5］Chica O M，Abarca H F.Computing Geostatistical Image Texture for Remotely Sensed Data Classification［J］.Computers and Geosciences，2000，26(4):373 －383.

［6］Dong P，Leblon B.Rock Unit Discrimination on Landsat TM，SIR－C and Radarsat Images Using Spectral and Textural Information［J］.int J Remote Sensing，2004，25(18):3745 －3768.

［7］沈远超，金成伟.西准噶尔地区岩浆活动与金矿化作用［M］.北京:科学出版社，1993.

［8］安 芳，朱永峰.新疆哈图金矿蚀变岩型矿体地质和地球化学研究［J］.矿床地质，2007，26(6):621 －634.

［9］Mandelbrot B B.Fractals Form，Chance and Dimension［M］.San Francisco:Freeman，1977.

［10］Pentland A P.Fractal Based Description of Natural Scenes［J］.IEEE Trans，1984:6(6):661 －674.

［11］李长江，麻土华，朱兴盛，等.矿产勘查中的分形、混沌与ANN［M］.北京:地质出版社，1999.

［12］King G.The Accommodation of Large Strains in the Upper Lithosphere of the Earth and Other Solids by Self－similar Fault Systems:The Geometrical Origin of b － value［J］.Pageoph，1983，121(5－6):761－815.

［13］皇甫岗，韩 明，王晋南.滇西北区断层分数维几何学的研究［J］.地震地质，1991，13(1):61 －66.

［14］曾联波，金之均，李京昌，等.柴达木盆地北缘断裂构造分形特征与油气分布关系研究［J］.地质科学，2001，36(2):241 －247.

［15］郭纯青，李文兴.岩溶含水介质与地下水系统理论研究［M］.桂林:广西师范大学出版社，1996.

［16］李 社，管太阳，曹双林，等.基于RIS与分形的下庄矿田线性构造空间特征分析［J］.遥感学报，2007，11(4):493 －499.

［17］余 勇.高分辨率卫星遥感在高龙金矿及其外围找矿中的应用研究［D］.桂林:桂林工学院，2005.

［18］金章东，卢新卫，张传林.江西德兴斑岩铜矿田断裂分形研究［J］.地质评论，1998，44(11):57 －61.

［19］夏玉成，樊怀仁，胡明星，等.霍州矿区断层构造的分形特征［J］.西安矿业学院学报，1997，17(1):22 －24.

［20］高明星.东天山遥感影像线性构造提取及统计分析［D］.乌鲁木齐:新疆大学，2005.

［21］Chaudhuri B B，Sarkar V.Texture Segmentation Using Fractal Dimension［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1995，17(1):72 －77.

［22］张哲儒，毛华海.分形理论与成矿作用［J］.地学前缘，2000，7(1):195－204.

［23］赵 旭.关于分形统计学研究的若干问题［J］.理论新探，2006(4):19－20.

［24］谢淑云，鲍佂宇.多重分形与地球化学元素的分布规律［J］.地质地球化学，2003，31(3):97 －102.

Fractal Application in Lithological Classification and Alteration Extraction

ZHENG Gui－ xiang1，3，CHI Tian － he1，LIN Qi－ zhong2
(1.Institute of Remote Sensing Applications，Chinese Academy of Sciences，Beijing 100101，China;2.Center for Earth Observation and Digital Earth，Chinese Academy of Sciences，Beijing 100086，China;3.Graduate University of Chinese Academy of Sciences，Beijing 100049，China)

In order to promote the application of multi－fractal theory to remote sensing exploration，this paper takes the West Junggar Region as the study area to build fractal dimension spectra by analyzing the characteristics of the region and the remote sensing image.Combined with spectra，the authors completed the lithologic classification and pyrite alteration extraction of the region.And then mineral targets of the region was identified with the support of the existing statistical data of mines and expert’s experience and knowledge.Practice has proved that the appropriate prospecting model and criteria established on remote sensing images of fractal theory and spectral characteristics can satisfactorily supply decision support to regional mineral exploration.

fractal;remote sensing prospecting;lithological classification;alteration information extraction;fractal dimension spectra

TP 79

A

1001－070X(2012)02－0110－06

郑桂香(1983－)，女，在读博士，主要研究方向为遥感空间信息共享。E－mail:littlelf@163.com。

(责任编辑:刁淑娟)

10.6046/gtzyyg.2012.02.20

2011－09－04;

2011－11－02