沥青路面加热型密封胶的低温黏弹性模型

李 峰，黄颂昌，石小培

(交通运输部公路科学研究院道路结构与材料交通行业重点实验室，北京100088)

0 引言

裂缝是沥青路面的主要病害之一，采用密封胶进行路面开槽灌缝，封闭路面裂缝，防止水渗入路面结构内部，是国际上公认的减缓路面病害出现、延长路面使用寿命的有效手段［1］.国内外普遍采用的裂缝修补材料是加热型密封胶，即橡胶改性沥青密封胶.与沥青材料类似，沥青基的加热型密封胶也是温度敏感性材料，部分材料在低温条件下容易变硬变脆、失去变形能力.目前，国内采用的加热型密封胶来源广泛，但使用效果不尽理想，特别是低温性能普遍较差，很多密封胶一到冬季即与裂缝壁撕裂，失去了防水的效果［2］.加热型密封胶的低温性能已经成为制约沥青路面灌缝技术发展的一个关键因素［3］.

国际上通行以ASTM D5329［4］的粘结试验评价沥青路面密封胶的低温性能.我国交通行业标准《路面橡胶沥青密封胶》(JT/T 740—2009)［5］中的低温拉伸试验也引自该试验.近年来，黏弹性力学(流变学)理论广泛应用于沥青和沥青混合料的低温抗裂性能研究.在此背景下，国外的一些学者也开展了基于黏弹性理论的密封胶低温性能研究［6－9］.低温黏弹性是反映加热型密封胶低温性能的重要特征，黏弹性所反映的实质是分子的运动及其结构的变化.黏弹性模型理论不仅能直观、形象地描述材料的宏观力学行为，也可以对其黏弹性特征进行定量分析，是研究沥青材料流变性能的有效方法［10］.笔者借助标准线性固体模型对密封胶的黏弹性能进行研究，推导常应变拉伸和应力松弛的理论方程，精确描述密封胶在低温条件下的应力－应变本构关系，为研究密封胶的低温性能提供理论基础.

1 试验方案

1.1 试件制作

参照JT/T 740制作拉伸试件，试件由水泥混凝土块和密封胶组成.水泥混凝土块采用石灰石集料，P.O32.5 的普通硅酸盐水泥，水灰比为0.49～0.55，混凝土水泥用量为(335 ±30)kg/m3.将制备的水泥混凝土放入标准混凝土养生室养生28 d，然后用切割机把水泥混凝土件切割成小条块，尺寸为75 mm×50 mm×25 mm，水泥混凝土块的抗拉强度应大于3 MPa.

用金属模块和水泥混凝土块围出一个50 mm×50 mm×15 mm的空隙，倒入密封胶，略高于水泥混凝土块顶面，在室温中冷却2 h，用热刮刀刮除多余灌缝胶，然后拆除金属模块，得到如图1所示的拉伸试件.笔者选用6种密封胶进行试验，制作的密封胶试件编号分别为H1～H6.

图1 拉伸试件Fig.1 Bond test specimen

1.2 试验程序

研究参照ASTM D5329的粘结试验进行，采用的拉伸试验机由万能材料试验机、低温箱和电脑组成，如图2所示.应力松弛的测量需要对试件施加阶跃式的应变，而采用万能材料试验机研究应力松弛时，拉伸到一定应变需要时间，因此，必须要考虑拉伸阶段的影响.在本文试验中，首先以恒定的速率对密封胶试件进行拉伸，密封胶的内应力逐步增加，达到一定伸长后维持在恒定应变，密封胶开始应力松弛，内应力逐步下降.

图2 拉伸试验机Fig.2 The bond tester

试验具体过程是：把如图1所示的密封胶试件置于低温箱中保温不少于4 h后，启动万能材料试验机，以0.05 mm/min速度拉伸密封胶试件，位移达到一定量后，停止拉伸进行应力松弛试验，试验过程保持规定的试验温度，试验结束后由电脑自动输出试验过程的应力－时间曲线.加热型密封胶对拉伸速率比较敏感，试验采用0.05 mm/min拉伸速率，这是国内外密封胶的标准拉伸速率，比较符合路面裂缝的实际运动速率.

2 黏弹性模型

2.1 玻尔兹曼叠加原理［11］

密封胶拉伸－应力松弛过程中的应力σ和应变ε随时间t的变化关系如图3所示.密封胶先以常应变速率伸长，应力逐渐增加.在t0时刻，密封胶应变达到ε0，然后保持应变不变，密封胶开始松弛，应力逐步下降.根据玻尔兹曼叠加原理，这相当于在应变ε1(t)随着时间变化的基础上，在t0时刻再叠加一个反向应变ε2(t)，ε2(t)=－(t－t0)，在t≥t0时，ε1(t)+ε2(t)=ε0.应变ε1(t)和ε2(t)所产生的应力分别为σ1(t)和σ2(t)，在 t≤t0时，密封胶的应力为 σ(t)=σ1(t);在t≥t0时，σ1(t)和 σ2(t)叠加即可得密封胶的松弛应力为σ(t)=σ1(t)+σ2(t).

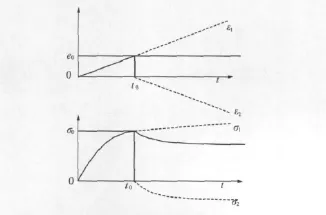
图3 玻尔兹曼叠加原理Fig.3 Boltzmann superposition principle

2.2 标准线性固体模型

标准线性固体模型由一个弹性元件和一个麦克斯维尔模型串联而成，是描述固体黏弹性特征的最简单有效的模型之一.该模型如图4所示，其微分型本构关系如式1所示［11］.

式中：σ、ε分别为模型的应力和应变;E1、E2分别为模型中弹性元件的弹簧模量;η为模型中黏性元件的黏度系数;分别为应力、应变对时间的导数;t为时间.

图4 标准线性固体模型Fig.4 Standard linear solid model

在常应变速率条件下，式(1)的应力解析解为

式中：σ1(t)为ε1(t)所产生的应力;为常应变速率.

则式(2)可简化为：

式中：a、b为模型系数;τ为模型的松弛时间.同理可得，ε2(t)所产生的应力为

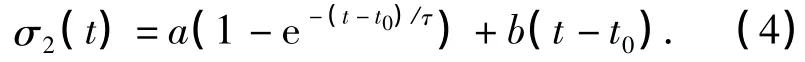
可得松弛阶段应力σ(t)为

3 试验结果及拟合分析

进行拟合首先需要对实验数据及异常点进行处理，初始阶段由于试件夹具松动等原因需要进行应力归零处理，对不同时刻应力值加减一个常数，使得时间t=0时，应力σ=0.采用统计分析软件进行非线性回归分析，拉伸过程根据式(3)，松弛过程根据式(5)，分别得到a、b和τ3个参数值.

对上述6种密封胶分别进行常应变拉伸－应力松弛试验，根据它们的低温拉伸试验情况，选择了3种不同的应变量，分别为：H1、H2的应变量为2.25 mm，H3、H4 的应变量为3.75 mm，H5、H6的应变量为6.90 mm.这是出于以下两方面因素的考虑：一是部分密封胶的低温性能较差，在达到较大应变之前即已经破坏，只能进行小应变试验;二是由于过大的应变容易导致密封胶出现塑性变形，因此应变不宜过大.所得试验数据与拟合曲线如图5所示，图中实线为试验数据曲线，虚线为拟合方程曲线.图5(a)为H1和H2拉伸达到2.25 mm应变后的松弛试验，图5(b)为H3和H4拉伸达到3.75 mm应变后的松弛试验，图5(c)为H5和H6拉伸达到6.90 mm应变后的松弛试验.表1给出了图5拟合曲线的方程及相关系数.

图5 拉伸－松弛过程的应力－应变拟合曲线Fig.5 The stress-strain fitting curves of extension-relaxation process

从图5可以看出，密封胶的拟合曲线与试验曲线拟合的很好，在表1中，各回归方程和试验数据的相关系数均在0.975以上，表明密封胶的回归方程与试验数据的相关性非常好.图5(a)中，H1和H2的应变为2.25 mm，H1和H2在拉伸阶段的曲线表现为曲率较大，即H1和H2相对表现为弹性较大、黏性较小;图5(b)中，H3和H4的应变为3.75 mm，H3和H4在拉伸阶段的曲线表现为曲率变小，即相对于 H1、H2，H3、H4表现为弹性减小、黏性增大;图5(c)中，H5和H6的应变为6.90 mm，H5和H6在拉伸阶段的曲线表现为曲率最小，即H5和H6表现为弹性最小、黏性较大;图5(c)中，H5在拉伸的最后阶段，应力开始下降，表明H5已经开始出现了少量的塑性变形.

完全符合理想标准线性固体模型的黏弹性材料，其拟合曲线和试验曲线应该是完全吻合的，其拉伸方程和松弛方程的回归系数也应该是完全一致的，但实际情况如图5和表1所示，出现了一定的差别.并且，当应变较小时，拟合曲线和试验曲线吻合的较好，拉伸方程和松弛方程的回归系数差别也较小;反之，当应变较大时，拟合曲线和试验曲线的差别有所增大，拉伸方程和松弛方程的回归系数差别也相应增大.分析认为，这是由于加热型密封胶在低温条件下不是完全理想的黏弹性材料，试验数据与模型理论存在一定的误差.当应变较小时，加热型密封胶更多地表现黏弹性，试验数据与模型理论误差较小;当应变较大时，加热型密封胶出现一定量的塑性变形，试验数据与模型理论误差也相应增大了.因此，为保证黏弹性模型能较为精确地反映密封胶的低温力学行为，进行拉伸－松弛试验时应控制密封胶的应变在一定范围之内.

表1 不同应变条件下密封胶的回归方程Tab.1 The fitting equations of sealants at different strains

4 结论

(1)根据玻尔兹曼叠加原理推导了标准线性固体模型在拉伸阶段和松弛阶段的理论方程，利用标准线性固体模型对加热型密封胶的常应变拉伸－应力松弛试验结果进行回归分析，得到的回归方程与试验数据吻合的较好，表明标准线性固体模型可以较为理想地描述密封胶的低温黏弹性力学行为.

(2)通过比较3种不同的应变量可知：在一定的应变范围内，应变越小，加热型密封胶的黏弹性特征越明显，标准线性固体模型的拟合精度越高;应变越大，加热型密封胶的塑性变形越明显，标准线性固体模型的拟合精度变低.

［1］GALEHOUSE L，KING H，LEACH D，et al.Preventive maintenance treatment performance at 14 years［C］//Transportation Research Record：Journal of Transportation Research Board.Washington，D C：National Research Council，2005.

［2］高建立，李林，宁杰，等.道路高分子聚合物密封胶低温性能实验方法研究［J］.公路交通科技：应用技术版，2006(1)：73 －74.

［3］李峰，黄颂昌，石小培.沥青路面裂缝密封胶的低温性能评价［J］.武汉理工大学学报，2011，33(8)：53－57.

［4］ASTM.D5329—2004，Standard Test Methods for Sealants and Fillers，Hot-Applied，For Joints and Cracks in Asphaltic and Portland Cement Concrete Pavements［S］.Philadelphia：ASTM，2004.

［5］交通运输部公路科学研究院.JT/T 740—2009，路面橡胶沥青灌缝胶［S］.北京：人民交通出版社，2009.

［6］AL-QADI I L，LOULIZI A，AREF S，et al.Modification of bending beam rheometer specimen for low-temperature evaluation ofbituminous crack sealants［C］//Transportation research record： Journalof Transportation Research Board.Washington，D C：National Research Council，2005.

［7］AL-QADI I L，YANG S H，DESSOUKY S，et al.Low temperature characterization of hot poured crack sealant using modified SHRP direct tensile tester［C］//Transportation research record：Journal of Transportation Research Board.Washington，D C：National Research Council，2007.

［8］SOLIMAN H，SHALABY A.Evaluation of joint and crack sealants based on cyclic loading and rheological properties［C］//2007 Annual Conf of the Transportation Association of Canada(TAC).Saskatoon，Canada：TAC，2007.

［9］SOLIMAN H，SHALABY A，KAVANAGH L.Performance evaluation of joint and crack sealants in cold climates using DSR and BBR tests［J］.Journal of Structural Engineering，ASCE，2008，20(7)：470－477.

［10］刘立新.沥青混合料粘弹性力学及材料学原理［M］.北京：人民交通出版社，2006.

［11］沈金安.沥青及沥青混合料［M］.北京：人民交通出版社，2001.