潜孔锤反循环钻进岩屑粒度分布规律

黄 勇，朱丽红，殷 琨，任 红

1.吉林大学建设工程学院，长春 130026 2.中国石油大学石油工程学院，山东青岛 266580 3.胜利石油管理局钻井工艺研究院，山东东营 267021

潜孔锤反循环钻进岩屑粒度分布规律

黄 勇1，朱丽红2，殷 琨1，任 红3

1.吉林大学建设工程学院，长春 130026 2.中国石油大学石油工程学院，山东青岛 266580 3.胜利石油管理局钻井工艺研究院，山东东营 267021

研究岩屑粒度分布规律有利于进一步分析潜孔锤反循环钻进的碎岩机理。采用分布函数和分形方法对反循环钻进产生的岩屑粒度分布进行描述，并得到岩屑粒度分布规律。结果表明：试验用岩屑的粒度分布符合Gandin－Schuhmann分布和Rosin－Rammler分布，其中岩屑颗粒更贴近于G－S分布；岩屑粒径遵循分形规律，可以用分形方法描述反循环钻进中岩屑粒度的分布特征。从岩屑粒度分布来看，大于5mm的颗粒占总质量的74.8%，表明潜孔锤球齿破碎岩石以体积破碎为主；块状颗粒分布在5～12mm，说明岩石的体积破碎存在大小差异，并伴随有重复破碎。

潜孔锤；反循环；岩屑；粒度分布；分形

0 引言

岩石破碎是岩石在外部荷载作用下，内部细微裂隙不断萌生、发展、汇集，直至相互贯通形成宏观块体的过程［1］。破碎产生的碎屑存在着尺寸和数量上的差异，它们的产生存在随机性，但也有规律可循。研究岩石破坏后岩屑的粒度分布规律，是探讨岩石破坏机理的重要手段，最终达到改进岩石破碎工艺、提高岩石破坏效率和降低碎岩能耗的目的。潜孔锤反循环钻进技术作为一种硬岩地层钻进成孔的高效手段，已广泛应用于水文、地质、地面工程等领域［2－3］。深入研究反循环钻进过程中产生的岩石破碎屑的粒度分布情况，有益于碎岩机理的研究，同时有助于进一步改进钻具结构，优化钻进参数。

目前对于粒度分布规律的研究方法很多，比较常用的有Gandin－Schuhmann（G－S）分布、Rosin－Rammler（R－R）分布、对数正态分布、指数分布等［4］。近年来，随着分形理论的快速发展，该理论也被引入到岩石破碎领域，用来描述岩石的损伤、断裂过程，研究表明岩石的破坏具有分形特征［4－8］。在前人研究的基础上，笔者通过现场试验获取反循环钻进产生的岩石破碎屑，并对岩屑进行筛分，利用分布函数和分形方法对岩屑粒度分布规律进行描述，通过岩屑粒度分布规律进一步分析潜孔锤反循环钻进碎岩机理。

1 潜孔锤反循环钻进技术

潜孔锤反循环钻进技术是冲击回转钻进的一种，其核心结构是贯通式潜孔锤，结构原理如图1所示：压缩空气沿双壁钻杆环状间隙输入，经上接头3推开逆止阀2进入潜孔锤外缸6与内缸7间的环状间隙，再经内缸上的进气孔B进入前后气室A和 C，推动活塞8往复运动，产生冲击力。前后气室内的工作废气经由活塞内孔与心管10外圆柱面之间的环形间隙进入反循环钻头15上部的环状空间，由钻头上的底喷孔和内喷孔排出，形成高速空气射流。潜孔锤钻进过程中，孔底岩石受到由压缩空气驱动孔底潜孔锤产生的高频冲击力和由钻杆传来的轴向压力和回转力共同作用，在动静多重载荷下产生有效体积破碎。冲击力是动荷载，轴向压力用来减少钻具反弹和提供预压力，水平回转力起到剪切碎岩和均匀破碎的作用。对岩石破碎产生的颗粒进行粒度分析，有助于了解各个力在碎岩中的作用，从而进一步分析潜孔锤的碎岩机理。

2 岩屑粒度分布试验

2.1 现场取样

取样钻进试验场地位于河南栾川钼矿，该矿是我国重要的钼矿生产基地，有矿产20多种，其中以钼、钨、铁、硫为主要矿物。矿区位于东秦岭钼多金属矿带内，地质构造发育，区内岩浆活动较为频繁，矿区围岩因受花岗质岩浆侵入影响，形成了有一定规模的热力变质岩（角岩）及接触交代变质岩（矽卡岩）。根据已有地质勘查报告，选取岩体较为完整的角岩地层进行取样试验，并利用旋流取样器收集钻进上返的岩屑。

本次钻进试验所钻地层岩性为透辉石角岩，该类岩石具有较大硬度，可钻性高，研磨性强，其物理力学性能指标为：密度3.42×103kg／m3，抗压强度280MPa，弹性模量6.0×104MPa，抗拉强度10 MPa，抗剪强度4MPa，可钻性Ⅶ级，研磨性Ⅴ级。

图1 贯通式潜孔锤结构原理图Fig.1 Schematic structure of run－through DTH hammer

试验所使用的钻探设备和机具如下：GSD－Ⅲ型钻机，Atlas Copco XRVS466型空气压缩机，钻具组合为SBC－89／44外平双壁钻杆＋GQ－108／44型贯通式潜孔锤＋Ф114反循环取样钻头（图2）。GQ－108／44贯通式潜孔主要技术参数包括：总长1255 mm，外径108mm，贯通孔直径44mm，活塞质量8.5kg，单次冲击功268J，冲击频率19Hz。反循环钻进过程中，钻机轴向钻压6～8kN，钻机转速33r／min，空压机输气量8～12m3／min。

图2 反循环取样钻头Fig.2 Reverse circulation drilling bit

2.2 筛分试验

由于现场收集的岩屑量较大，先将岩石样品采用环锥法混合再用四分法缩分，经过几次缩分后将所剩岩样进行手动筛分，筛网孔径分别为0.5、2、3、5、7、10mm，其中，0.5、2mm为方孔筛，其余为圆孔筛。岩屑的筛分结果见表1。经筛分后的岩屑按照筛孔尺寸依次排列，对应的实物照片如图3所示。

表1 岩屑粒径质量分布Table 1 Grain size mass distribution of rock samples

3 岩屑粒度描述

3.1 分布函数描述

描述岩石粒度分布规律的函数很多，其中G－S分布和R－R分布应用广泛［9］。一般认为G－S分布贴近细粒度区，而R－R分布更贴近粗粒度区［10］。

G－S分布函数：

式中：x为粒度；y为x的筛下累积质量分数；a为粒度的分布指数；k为粒度的分布特征值。

R－R分布函数：

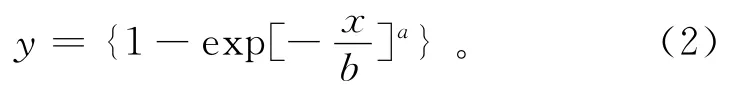
式中：x为粒度；y为x的筛下累积质量分数；a为分布指数；b为粒度特性系数。

图3 筛分后岩屑实物照片Fig.3 Photo of rock samples after sieving

通过筛分将岩样按粒径尺寸划分为7个区段，根据筛孔尺寸与筛下累积质量分数的一一对应关系，绘制岩屑的粒度分布函数曲线。粒径小于0.5 mm和大于10mm的岩样在分布函数拟合过程中引起的误差较大，在绘制分布函数曲线图时暂不考虑上述两区段。

公式（1）可转换为

lny＝alnx－alnk。（3）

此时G－S函数改写为线性函数Y＝AX＋B的形式。由表1筛分结果和式（1）绘制出岩样的粒径分布散点图和回归曲线，如图4所示。

将式（2）改写成Y＝AX＋B形式，结果如下：

ln［－ln（1－y）］＝alnx－alnb。（4）根据筛分结果，绘制出岩样的粒径分布散点图和回归曲线（图5）。

图4 岩样粒度G－S分布Fig.4 Grain size G－S distribution of rock samples

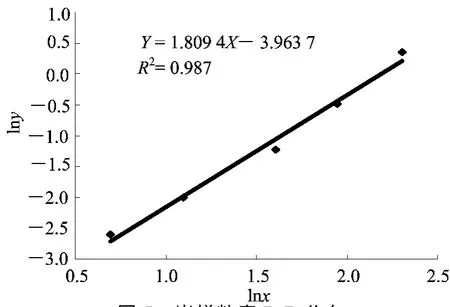
图5 岩样粒度R－R分布Fig.5 Grain size R－R distribution of rock samples

由图4可知，回归系数R的绝对值为0.999 1，线性回归直线表达式：Y＝1.473 8 X－3.683 1。由此推算分布函数的分布指数a为1.473 8，粒度分布特征值k为12.167。当粒度x取k时，代入式（3），得筛下累积质量分数y为1，说明岩屑的最大粒径为12.167mm。

由图5可得到R－R分布下的回归直线Y＝1.809 4 X－3.963 7，回归系数R的绝对值为0.993 5，则分布函数的分布指数a为1.809 4，分布特征值b为8.940 6。b也称中位径，表示岩屑筛下累积质量分数为50%时的粒径尺寸为8.940 6 mm。

从G－S分布和R－R分布的趋势线可以看出，破碎产生的岩屑对于两种分布都具有很好的相符性，拟合曲线的回归系数均大于0.99，这是由岩屑尺寸处于较小粒径区间决定的，其中岩屑粒径更贴近GS分布。筛分结果也表明岩屑粒径均小于20mm，由拟合结果可知其最大尺寸约为12mm。

3.2 分形维数描述

由连续条件下的分形定义［11］可知：

式中：R为岩屑特征尺度；N为特征尺度大于等于R的岩屑数目；C为常数；D为分形维数。

设上返岩屑总质量为M，M（R）为筛网孔径为R时筛下岩屑的累积质量，则有

同时，由岩屑质量与数目关系：

对比式（5）、（6）和（7），则存在

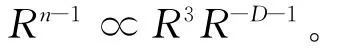
从而分形维数

由式（6）绘制M（R）／M－R双对数坐标系下的曲线图，如图6所示。n为回归曲线斜率，其值为1.473 8，由式（8）可得分维数D为1.526 2。

图6 岩样粒度分形曲线Fig.6 Grain size fractal curve of rock samples

由分形维数D和回归曲线斜率n关系可知：当岩样的筛分粒度范围一定时，n值越大，拟合曲线斜率越大，维数D越小，岩样中粗颗粒含量越大；相反，n值越小，拟合曲线斜率越小，维数D越大，岩样中细颗粒含量越大。分形维数能够反映破碎后岩屑的粒度特征，可以作为描述岩石粒度分布的一个定性指标。

3.3 碎岩机理分析

潜孔锤反循环钻进具有冲击和回转两种碎岩手段，由于回转速度较低，碎岩以冲击破碎为主。钻头球齿受力如图7所示。一般认为，在冲击力作用下，钻头球齿破碎岩石主要包括压碎和剪崩两部分，钻进中球齿底部岩石受到较高的冲击荷载，形成高应力区，将下部岩石压碎，产生较小块岩屑和岩粉；球齿临近的岩石受到挤压发生剪切破坏，产生大体积岩屑，在压头底部形成倒锥形破碎穴。根据筛分后的质量分布表可知，粒径范围在7～10mm的岩屑质量最大，大于7mm岩屑占总质量54.3%，大于5mm的岩屑占总质量的74.8%，而小于2mm的岩屑质量分数约为11%，明显看出球齿的挤压剪崩作用是碎岩的关键手段，这也是反循环钻进具有较高钻进效率的主要原因。

4 结论

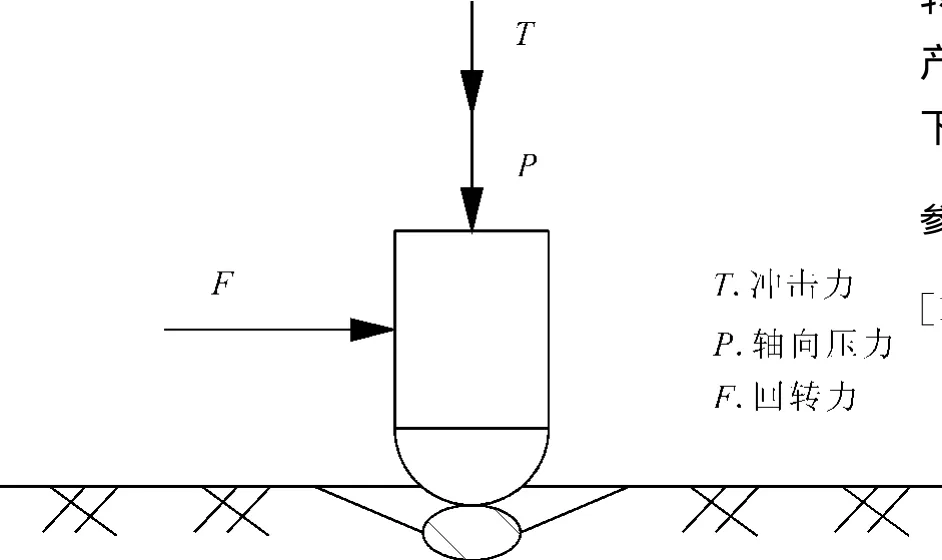
图7 钻头球齿受力示意图Fig.7 Schematic diagram of drill tooth force

岩屑中块状颗粒主要是由体积剪切破坏产生的，其粒径范围集中在5～12mm，说明球齿在破碎岩石过程中，每次冲击产生的破碎坑体积存在大小差异，岩石的最终破碎是多次冲击累积的结果，几次小的体积破碎后，会产生一次大的体积破碎。岩屑中没有单颗大尺寸颗粒，级配较好，这是由于岩屑受到钻头中心挡块限制，大块颗粒不能进入中心通道上返，而在孔底被钻头二次或多次破碎，这种破碎产生的岩屑与初次破碎的岩屑具有相同的粒度分布规律。

1）通过现场试验获取潜孔锤反循环钻进所产生的岩石破碎屑，并利用筛分法对岩屑进行粒度划分，得到岩屑的粒径－质量分布关系。

2）采用粒度分布函数和分形理论对岩屑的粒度分布进行描述，得到钻进条件下岩石粒度分布规律。从粒度分布曲线可知，岩屑符合G－S分布与R－R分布，其中更贴近G－S分布，说明岩屑粒径处于较小粒度区间内。岩屑粒度分布具有分形特征，试验用岩屑的分形维数为1.526 2，分形维数可作为表征岩屑粒度分布的度量指标。

3）从岩屑的粒度分布来看，粒径大于7mm的颗粒超过总质量的一半，表明潜孔锤钻进以体积破碎为主；岩屑块度大小不一，粒径主要分布在5～12 mm，说明岩石的体积破碎存在大小差异，并伴随有重复破碎。

4）潜孔锤反循环钻进中，随着冲击频率、钻压、转速等钻进参数、设备机具和地层的不同，必然对所产生岩屑的粒径存在一定的影响，这部分研究将是下一步工作的重点。

（References）：

［1］ 高峰，谢和平，巫静波.岩石损伤和破碎相关性的分形分析［J］.岩石力学与工程学报，1999，18（5）：497－502.

Gao Feng，Xie He－ping，Wu Jing－bo.Fractal Analysis of the Relation Between Rock Damage and Rock Fragmentation［J］.Chinese Journal of Rock Mechanics and Engineering，1999，18（5）：497－502.

［2］ 朱丽红，殷琨，刘建林，等.反循环气体钻井压力计算分析［J］.钻井液与完井液，2009，26（4）：34－37.

Zhu Li－hong，Yin Kun，Liu Jian－lin，et al.Pressure Calcultion and Analysis of Reverse Circulation Air Drilling［J］.Drilling Fluid ＆Comoletiong Fluid，2009，26（4）：34－37.

［3］ 朴金石，殷琨，范黎明.利用神经网络法预测风动潜孔锤钻速［J］.吉林大学学报：地球科学版，2009，39（5）：882－885.

Piao Jin－shi，Yin Kun，Fan Li－ming.Neural Network Method in the Penetration Rate Prediction of Percussive Drilling［J］.Journal of Jilin University：Earth Science Edition，2009，39（5）：882－885.

［4］ 王谦源，姜玉顺，胡京爽，等.岩石破碎体的粒度分布与分形［J］.中国矿业，1997，6（3）：50－55.

Wang Qian－yuan，Jiang Yu－shun，Hu Jing－shuang，et al.Size and Fractal Distributions of Rock Fragments［J］.China Mining Magazine，1997，6（3）：50－55.

［5］ 谢和平.分形几何及其在岩土力学中的应用［J］.岩土工程学报，1992，14（1）：14－24.

Xie He－ping.Fractal Geometry and Its Application to Rock and Soil Materials［J］.Chinese Journal of Geotechnical Engineering，1992，14（1）：14－24.

［6］ 高峰，谢和平，赵鹏.岩石块度分布的分形性质及细观结构效应［J］.岩石力学与工程学报，1994，13（3）：240－246.

Gao Feng，Xie He－ping，Zhao Peng.Distribution of Rock Fragments and the Influence of Meso－Structure［J］.Chinese Journal of Rock Mechanics and Engineering，1994，13（3）：240－246.

［7］ 周金枝，徐小荷.分形几何用于岩石损伤扩展过程的研究［J］.岩土力学，1997，18（4）：36－40.

Zhou Jin－zhi，Xu Xiao－he.Fractal Analysis of Damage Evolution Process of Rock［J］.Rock and Soil Mechanics，1997，18（4）：36－40.

［8］ 李廷芥，王耀辉，张梅英，等.岩石裂纹的分形特征及岩爆机理研究［J］.岩石力学与工程学报，2000，19（1）：6－10.

Li Ting－jie，Wang Yao－hui，Zhang Mei－ying，et al.Fractal Properties of Crack in Rock and Mechanism of Rock－Burst［J］.Chinese Journal of Rock Mechanics and Engineering，2000，19（1）：6－10.

［9］ 徐小荷，余静.岩石破碎学［M］.北京：煤炭工业出版社，1984：33－57.

Xu Xiao－he，Yu Jing.Rock Breaking Mechanics［M］.Beijing：China Coal Industry Publishing House，1984：33－57.

［10］ 李士斌，闫铁，李玮.地层岩石可钻性的分形表示方法［J］.石油学报，2006，27（1）：124－127.

Li Shi－bin，Yan Tie，Li Wei.Fractal Representation of Rock Drillability［J］.Acta Petrolei Sinica，2006，27（1）：124－127.

［11］ 谢和平.分形－岩石力学导论［M］.北京：科学出版社，1996：168－261.

Xie He－ping.Introduction to Fractal－Rock Mechanics［M］.Beijing：Science Press，1996： 168－261.

Grain Size Distribution Law of Cuttings in DTH Hammer Reverse Circulation Drilling

Huang Yong1，Zhu Li－hong2，Yin Kun1，Ren Hong3

Research on grain size distribution law would be helpful to further analysis on rock broken mechanism of DTH hammer reverse circulation drilling.The grain size distribution of cuttings in DTH hammer reverse circulation drilling was described by distribution and fractal function，and its distribution law was obtained.Results showed that the grain size distribution of cuttings conform to Gandin－Schuhmann distribution and Rosin－Rammler distribution，and much closer to G－S distribution.The cutting grain size distribution characteristics of reverse circulation drilling follow the fractal rule and can be described by fractal method.The grain size distribution indicates that the total mass of cuttings greater than 5mm is 74.8%，which shows a predominant volume broken of rock by DTH hammer.The size of massive particle is between 5mm to 12mm，indicating the size difference in volume broken accompanied by repeated crushing.

DTH hammer；reverse circulation；cutting；grain size distribution；fractal

book=2012,ebook=643

P634.1

A

1671－5888（2012） 04－1119－06

2011－10－20

山东省自然科学基金项目（ZR2011EEQ012）；高等学校博士学科点专项科研基金项目（20110133120013）；中央高校基本科研业务费专项资金项目（27R1202001A）

黄勇（1981－），男，博士研究生，主要从事多工艺冲击回转钻进技术研究，E－mail：huangyongjlu＠163.com。

1.College of Construction Engineering，Jilin University，Changchun 130026，China 2.School of Petroleum Engineering，China University of Petroleum，Qingdao 266580，Shandong，China 3.Drilling Technology Research Institute，Shengli Oilfield，Dongying 267021，Shandong，China