裂缝性地层声波测井的联合时频特征
2012-09-06王祝文王晓丽刘菁华张雪昂
王祝文,王晓丽,2,刘菁华,张雪昂,向 旻,杨 闯
1.吉林大学地球探测科学与技术学院,长春 130026 2.吉林大学学报编辑部,长春 130026
裂缝性地层声波测井的联合时频特征
王祝文1,王晓丽1,2,刘菁华1,张雪昂1,向 旻1,杨 闯1
1.吉林大学地球探测科学与技术学院,长春 130026 2.吉林大学学报编辑部,长春 130026
裂缝性油气藏越来越受到人们的重视,如何有效地识别和评价裂缝性地层也成为人们关注的一个焦点。Cohen类时频分析方法具有同时对信号的时间和频率进行分析的优点,同时Hilbert-Huang变换(HHT)中的经验模态分解(EMD)方法能将信号分解为有限个具有单分量特性的固有模态函数(IMF),可以满足Cohen类时频分析对信号单分量的要求。尝试将这两种方法联合应用于阵列声波信号特性的提取,对地层不同性质裂缝的信号能量的时频分布特征进行分析,结果显示了这种联合时频分析方法在不同的裂缝性质地层中有不同的表现特征,对于实现裂缝性地层分析和评价具有一定的现实意义。
裂缝性地层;声波测井;Cohen时频分析;Hilbert-Huang变换;经验模态分解;联合时频特征
0 引言
地层裂缝特征描述是裂缝性油气藏的一项重要研究内容,至今仍缺乏有效的测井评价方法。多极子阵列声波测井以其三维柱体测量、探测深度大的优势,可获取极为丰富的地层信息[1-13];但由于裂缝性地层中的声波传播机理不清,因而测量记录的信息远远没有被充分有效利用。充分挖掘其所包涵的信息,并将其所蕴涵的特征参数用于实际测井资料的处理分析和地层评价是非常有意义的。对所获得的测井信息,怎样更加有效地进行处理和分析已成为阵列声波测井的主要任务。笔者提出采用联合时频分析方法对实际测井得到的声波数据进行处理。首先对声波测井信号做经验模态分解(empirical mode decomposition,EMD),将声波测井信号分解成多个固有模态函数(intrinsic mode functions,IMF)分量;根据Huang等[14-15]的定义,EMD分解后得到的不同阶的IMF分量应该是单分量信号,这些信号在同一时间只对应着某一个频率,而且每个IMF分量都具有各自的时间特征,处于不同的频率范围内。而常用的Cohen类时频分析,虽然在不同的领域里取得了许多有用的成果,但是,这类方法在分析多分量信号时产生交叉项这一问题严重地制约了其广泛的应用。
本文中所采用的这种分析方法在一定程度上解决了直接使用Cohen类时频分布分析多分量信号时产生交叉项这一问题,通过EMD处理,有效地把不同频率的信号分解到各阶IMF分量中,这样就可以避免Cohen类时频分析方法在使用时会产生交叉项的难题。根据这个思路,笔者对实际测井中得到的全波列数据进行处理,期望能够从中获得不同性质裂缝的时频分布特征。
1 时频分析方法
1.1 Cohen类时频分布
Cohen类就是具有时(频)移不变性的时频分布类[16-17],而平滑伪Wigner-Ville分布(SPWD)是Cohen类二次型时频分布的一个特例。SPWD分布与线性的方法相比,时频分辨率一般较高,但是这种分布对多分量信号存在着固有的交叉项困扰。信号z(t)的Cohen类时频分布的表达式为
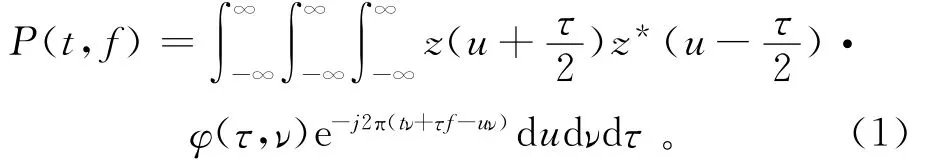
式中:t为时间(s);f为频率(Hz);z*(t)为z(t)的共轭函数;u,ν,τ为积分变量;φ(τ,ν)为时频分布核函数。当φ(τ,ν)=1时,Cohen类分布就变成了Wigner-Ville分布,它是Cohen类的成员,而且是最简单的一种。而SPWD的表达式为
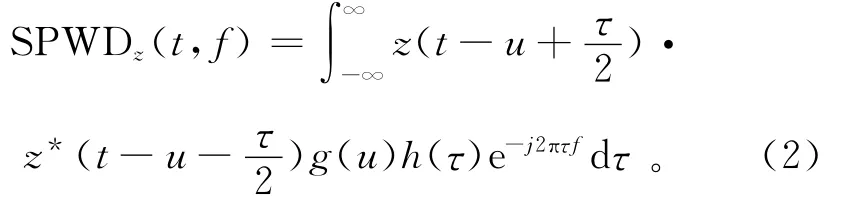
式中:g(u),h(τ)是2个实偶窗函数。
1.2 HHT变换
Hilbert-Huang变换(HHT)是由美籍华人Huang等[14-15]于1998年提出的一种新的信号处理和信息提取方法。该方法依据数据本身的特征将信号分解为有限个固有模态函数(IMF),其创新就在于先通过EMD法将信号分解为单分量信号,再通过HHT变换分别计算每个分量的各种特性。同其他时频分析方法相比,HHT变换在提取声波测井信号中应该具有相对明显的优越性,能提取到更多、更接近实际的地层裂缝的时频特性。
2 阵列声波测井信号的联合时频特征
由HHT变换的定义可知[14-15],经过EMD分解得到的每一个IMF分量都有不同的振幅和频率,获得的IMF按频率顺序是从高至低分布的,因此,IMF分量都有具体的物理意义。对于阵列声波信号而言,通过研究[9]可知:IMF1为主要代表的纵波以及部分横波分量,IMF2为横波和伪瑞利波分量,IMF3为高频斯通利波和伪瑞利波分量,IMF4为低频斯通利波分量,IMF5-IMF7为后续的各种波分量,Res为信号本身微弱的趋势或仪器的漂零。EMD分解获得的IMF时序曲线大体上为单一谐波,这个是Hilbert变换进行时频估计的基础。同时,这也满足了Cohen类时频分布单分量信号的要求[17]。因此,可以尝试联合使用这2种方法,对裂缝性信号进行分析,探求其规律。
图1是大陆科学钻探(CCSD)主孔460m处测量得到的阵列声波测井数据,对该点的声波信号以及各IMF分量分别做SPWD变换,以此对比分析其特点。
从图1中可以看出,如果对整个原始波列数据进行SPWD分析,在分布图中某些幅值较小的信号在图中显示不出来,这也表明仅仅采用SPWD方法难以区分信号中所蕴含的详细信息。而各IMF分量的SPWD分布则显示了各个分波的细节,可以详细地显示数据的时频特征。如前所述,IMF1分量主要为纵波与横波的信号,纵波相对于横波而言幅值较小,在图上显示不是很明显,图中主要显示的横波出现在1 800~3 000μs,其主频为6kHz左右。主要表示横波与伪瑞利波信号的IMF2分量出现在1 800~3 100μs,主频约为4kHz;高频斯通利波信号IMF3出现在1 800~3 400μs,主频为3kHz左右;低频斯通利波信号IMF4持续时间较长,为1 400~3 500μs,主频为1.8kHz左右;IMF5主要是斯通利波与泥浆波等后续波的叠加,持续时间长,为1 400~3 800μs,主频为1kHz左右。
根据HHT提出时的理论,经EMD分解后,得到的各IMF分量在同一时间一般只对应一个频率成分;这样的话就可以解决直接使用Cohen类时频分布直接分析多分量信号存在交叉项这一问题,得到比较准确的时频信息。
另外,根据HHT变换的理论,通过笔者的研究[7],EMD分解出的前几个IMF分量蕴含了原始波列信号中的最显著信息。从IMF1至IMF4,依次表现出了纵波、横波、斯通利波的相关特征;而由于斯通利波与地层裂缝信息密切相关,也就是说,斯通利波对地层的裂缝发育程度相对敏感。因此,可以通过斯通利波来研究其时频分布特征。而前文已经说明,IMF3和IMF4主要表现了斯通利波的信息,所以,笔者专门分析这2个分量的SPWD时频分布特征。
3 裂缝地层的联合时频分布特征
根据研究[7],阵列声波全波列经EMD分解后,一般可以形成7~8个IMF分量和1个残量。根据前面的分析,地层裂缝特征主要是与斯通利波密切相关,因此,将分解得到的IMF分量中与斯通利波有关的分量IMF3和IMF4进行SPWD变换,得到SPWD时频分布图(图2,图3)。
图2是大陆科学钻探主孔670m测井信号经EMD分解后IMF3和IMF4的SPWD时频分布图。这一段长达30余m的岩层为蛇纹岩,在岩心地质编录上,660m及680m处的蛇纹岩含有石榴石。根据声电成像解释结果,在这一层段,基本上没有构造现象出现。从图中可以看出:IMF3为高频斯通利波信号,时间跨度2 000~3 200μs,主要出现在2 500μs左右,其主频为2kHz左右;IMF4为低频斯通利波信号,持续时间较长,为1 000~4 200μs,主频为1.2kHz,主要在2 500μs处出现。这与前面图1中IMF3和IMF4有着明显的差别。
图3a为520m处的IMF3和IMF4的SPWD时频分布图。根据地质岩心编录及成像成果图解释,其上部516~519m处有一明显的构造现象。受该构造的影响,所测量得到的斯通利波发生了明显变化。从图中可以看出:高频斯通利波信号分量IMF3,出现在1 700~3 100μs,主频为1.7kHz左右;低频斯通利波信号分量IMF4,持续时间较长,为1 200~4 400μs,主频为1.0kHz,而且主要集中在4 000μs附近。这与前面图2中IMF3和IMF4有着明显的差别,同时也反映了受构造的影响,低频斯通利波频率降低,到达的时间也相应地延后了很多。
图3b为主孔600m处的IMF3和IMF4的SPWD时频分布图。从岩心编录给出的结论中可以知道,该处应该是金红石榴辉岩与多硅白云母榴辉岩的一个岩性分界面。从图中可以看出:高频斯通利波信号分量IMF3,出现在1 400~3 200μs,主频为2.1kHz左右;低频斯通利波信号分量IMF4,持续时间较长,为1 400~3 900μs,主频为1.2 kHz,而且主要集中在2 500μs附近。这种岩性界面的特征与图3a中IMF3和IMF4有着不一样的表现。
图3c所显示的是主孔605m处的的IMF3和IMF4的SPWD时频分布图。由声电成像解释结果及岩心编录知道,这是一个典型的构造破碎带。由于破碎带对声波能量的强烈吸收,其斯通利波的SPWD时频分布与前面的几处完全不一样。IMF3和IMF4分量都明显地出现2个峰值。IMF3代表的斯通利波的峰值一个出现在1 500~2 500μs,主频为2.5kHz,另一个出现在3 100~4 100μs,主频为1.8kHz左右;IMF4的一个峰值出现在0~800 μs,主频为1.9kHz,另一个峰值出现在1 700~3 800μs,主峰出现在2 600μs,主频为1.6kHz。这些特征,与前文所描述的裂缝特征完全不一样。这个特征也直接反映了地层的破碎程度,这与图3d所表现的时频特征相类似。
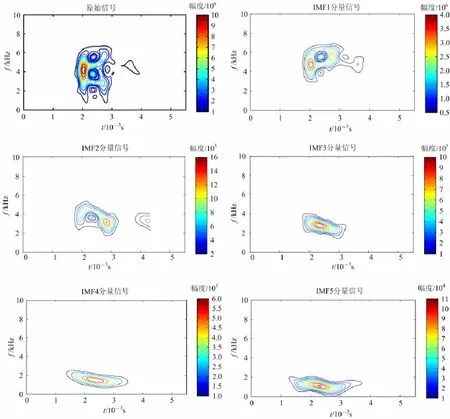
图1 CCSD井460m声波信号的SPWD时频分布Fig.1 The SPWD of array acoustic logging signal at 460mof CCSD hole
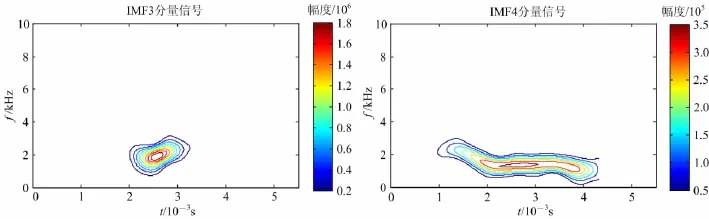
图2 CCSD井670m声波信号IMF3、IMF4的SPWD时频分布Fig.2 The SPWD of IMF3and IMF4signals at 670mof CCSD hole
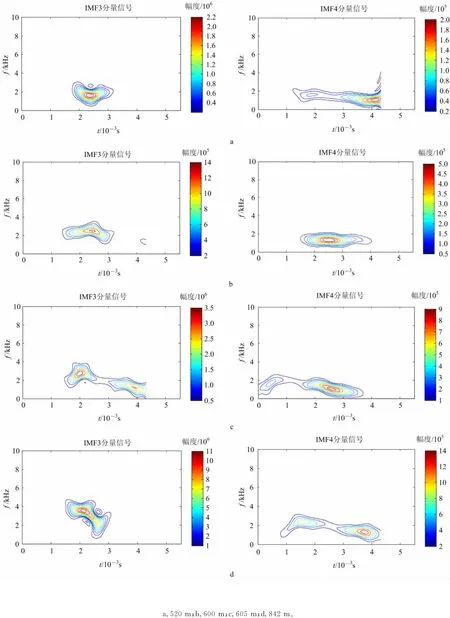
图3 CCSD井声波信号及其SPWD时频分布Fig.3 The SPWD of IMF3and IMF4signals at of CCSD hole
图3d是大陆科学钻探主孔842m的IMF3和IMF4的SPWD时频分布图。成像测井解释结果认为这是一段强烈破碎的层段,岩心编录表明这部分的构造现象很复杂。而图3d的阵列声波测井原始波列就是在这构造现象最复杂的地方选择的。与图3c相比,IMF3显示的特征不同,主要的峰值出现在1 500~3 100μs,主频比较高,接近4kHz;IMF4显示了2个峰值:一个出现在1 000~2 500μs,主频为2.2kHz,另外一个峰值出现在3 000~4 200μs,主频为1.8kHz左右。低频斯通利波的这个特征,与图3c一样,也出现了2个峰值;但是,从出现时间上、频率分布上的表现有其特有的特征。由于地层的强烈破碎,低频斯通利波的主要频率出现在3 800 μs,在时间上与图3c相比明显延后。
4 讨论与结论
1)对于阵列声波信号所包涵的信息,利用SPWD时频分析方法对整个波列进行分析,不能将它们分别显现出来。而经过EMD分解后得到的IMF分量的SPWD时频分布,对于纵波、横波、斯通利波、伪瑞利波以及后续的波,都可以给出明确的物理意义。
2)图3所显示的代表斯通利波的SPWD时频分布表明,对于不同类型的裂缝,无论是在高频还是低频斯通利波的SPWD时频分布图上,都有不同的反映。这是单从声波时域波列或频域中很难获取的信息。因此,在声波对地层裂缝的识别和评价中,联合时频分析具有其独特的优势。
3)对于裂缝性地层,由于声波信号在传播过程中受到破碎地层强烈的吸收,造成斯通利波的主频向低频方向移动。对于不同性质的裂缝、高频和低频斯通利波的时频特征差别很明显,根据这些特征,可以对地层裂缝进行识别。而对于裂缝的特征(宽度、分布密度、长度等)还有待于进一步的研究。
4)通过文中的实例分析可以看出,尽管HHT这种新的技术方法还有许多亟待改进的地方[18],笔者提出的结合Cohen类时频分析以及HHT分析两者的优点,对阵列声波信号所蕴含的裂缝特性的提取应该是一种较为有效的方法。
(References):
[1] 江玉龙,王祝文,伍东.阵列声波处理技术的研究与应用[J].地球物理学进展,2009,24(1):246-253.
Jiang Yu-long,Wang Zhu-wen,Wu Dong.Research and Applications of High Definition Array Acoustic Processing Techniques[J].Progress in Geophysics,2009,24(1):246-253.
[2] 王祝文,刘菁华,聂春燕.基于Choi-Williams时频分布的阵列声波测井信号时频分析[J].地球物理学进展,2007,22(5):1481-1486.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.Time-Frequency Analysis of Array Acoustic Logging Signal Based on Choi-Williams Energy Distribution[J].Progress in Geophysics,2007,22(5):1481-1486.
[3] 王祝文,刘菁华,聂春燕.时频分析的重排方法及其在声波测井信号处理中的应用[J].吉林大学学报:地球科学版,2007,37(5):1042-1046.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.The Reassignment Method Based on Time-Frequency Analysis and Its Application in the Array Acoustic Logging Data Processing[J].Journal of Jilin University:Earth Science Edition,2007,37(5):1042-1046.
[4] 王祝文,刘菁华,聂春燕.阵列声波测井信号的时频局域相关能量分析[J].吉林大学学报:地球科学版,2008,38(2):341-346.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.Array Acoustic Logging Signal Analysis Based on the Local Correlation Energy[J].Journal of Jilin University:Earth Science Edition,2008,38(2):341-346.
[5] 张学涛,王祝文,原镜海.利用时频分析方法在阵列声波测井中区分油水层[J].岩性油气藏,2008,20(1):101-104.
Zhang Xue-tao,Wang Zhu-wen,Yuan Jing-hai.Using Time-Frequency Analysis to Identify Oil and Water Layers in Array Acoustic Logging[J].Lithologic Reservoirs,2008,20(1):101-104.
[6] 王祝文,刘菁华,聂春燕.基于Hilbert-Huang变换的阵列声波测井信号的时频分析[J].地球科学:中国地质大学学报,2008,33(3):387-392.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.Time-Frequency Analysis of Array Acoustic Logging Waveform Signal Based on Hilbert-Huang Transform[J].Earth Science:Journal of China University of Geosciences,2008,33(3):387-392.
[7] 王祝文,刘菁华,聂春燕.Hilbert-Huang变换在提取阵列声波信号动力特性中的应用[J].地球物理学进展,2008,23(2):450-455.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.Application of Hilbert-Huang Transform in ExtractingDynamic Properties of Array Acoustic Signals[J].Progress in Geophysics,2008,23(2):450-455.
[8] 王祝文,刘菁华,聂春燕.纵波频谱特征与裂缝带关系初探:在中国大陆科学钻探中的应用[J].吉林大学学报:地球科学版,2008,38(6):1065-1069.
Wang Zhu-wen,Liu Jing-hua,Nie Chun-yan.Primary Study on the Relationship Between Primary Wave Frequency Characteristics and Structural Zone:Its Applications in the CCSD[J].Journal of Jilin University:Earth Science Edition,2008,38(6):1065-1069.
[9] Wang Zhu-wen,Liu Jing-hua,Yue Chong-wang,et al.The Filtering Character of Hilbert-Huang Transform and Its Application in Acoustic Log Waveform Signal Processing[J].Applied Geophysics,2009,6(1):8-16.
[10] 李晓春,王祝文,岳崇旺,等.Hilbert-Huang变换在提取声波测井信号储集特性的应用[J].岩性油气藏,2009,21(1):107-111.
Li Xiao-chun,Wang Zhu-wen,Yue Chong-wang,et al.Application of Hilbert-Huang Transform in Extracting Reservoir Properties of Array Acoustic Signals[J].Lithologic Reservoirs,2009,21(1):107-111.
[11] 陈博涛,王祝文,丁阳,等.Hilbert-Huang变换在阵列声波测井信号时频分析中的应用[J].岩性油气藏,2010,22(1):93-97.
Chen Bo-tao,Wang Zhu-wen,Ding Yang,et al.Application of Hilbert-Huang Transform in Time-Frequency Analysis of Array Acoustic Signals[J].Lithologic Reservoirs,2010,22(1):93-97.
[12] 陈博涛.EMD分解联合时频分析在阵列声波信号中的应用[D].长春:吉林大学,2010.
Chen Bo-tao.Application of the EMD Joint Time-Frequency Analysis in Array Acoustic Signal[D].Changchun:Jilin University,2010.
[13] 张学涛.时频分析方法在提取阵列声波测井信息中的应用[D].长春:吉林大学,2008.
Zhang Xue-tao.Application of Time-Frequency Analysis to Pick-Up Information in Array Acoustic Logging[D].Changchun:Jilin University,2008.
[14] Huang N E,Sheen Z,Steven R L,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J].Proc R Soc Lond A,1998,454:903-995.
[15] Huang N E,Sheen Z,Long S R.A New View of Nonlinear Water Waves:the Hilbert Spectrum[J].Annual Review of Fluid Mechanics,1999,31:417-457.
[16] 张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.
Zhang Xian-da,Bao Zheng.Analysis and Process of Non-Stationary Signal[M].Beijing:Defense Industry Press,1988.
[17] Leon Cohn.Time-Frequency Analysis:Theory and Applications[M].Englewood Cliffs:Prentice Hall,1994.
[18] 熊学军,郭炳火,胡筱敏,等.EMD方法和Hilbert谱分析法的应用与探讨[J].黄渤海海洋,2002,20(2):12-21.
Xiong Xue-jun,Guo Bing-huo,Hu Xiao-min,et al.Application and Discussion of Empirical Mode Decomposition Method and Hilbert Spectral Analysis Method[J].Advances in Marine Science,2002,20(2):12-21.
Joint Time Frequency Characteristics of Array Acoustic Logging Signals on Fractured Formation
Wang Zhu-wen1,Wang Xiao-li1,2,Liu Jing-hua1,Zhang Xue-ang1,Xiang Min1,Yang Chuang1
1.College of GeoExploration Science and Technology,Jilin University,Changchun 130026,China 2.Editorial Department of Journal,Jilin University,Changchun 130026,China
Fractured reservoir become more and more important role in reservoir exploration,and how to identify and evaluate this kind of reservoir is one of the focuses point in logging evaluation.Because of the Cohen time-frequency analysis method behave the advantages to analysis signals both in time and frequency domain,and the Hilbert-Huang transform(HHT)can be decomposed any signals into a finite number of intrinsic mode functions(IMF),since the IMF has the single component characteristics,this characteristics satisfied the need for Cohen time-frequency analysis method.The authors make use of these two advantages to extract the useful properties of array acoustic logging signals,the new method is used in extracting the fractured properties embedded in the array acoustic signals,the tested results had showed this method can effective extracting the time-frequency distribution characteristics of fractured formation.And this joint time frequency analysis method can further be used to extract more and more information embedded in the array acoustic logging signals to evaluate the reservoir properties.
fractured formation;acoustic logging;Cohen time-frequency analysis;Hilbert-Huangtransform;empirical mode decomposition;joint time frequency characteristics
book=2012,ebook=704
P631.8
A
1671-5888(2012) 04-0914-07
2012-04-25
国家自然科学基金项目(40874059)
王祝文(1961-),男,教授,博士,博士生导师,主要从事地球物理测井、核地球物理、测井新方法新技术等方面的解释理论和方法的教学与科研工作,E-mail:wangzw@jlu.edu.cn
刘菁华(1963-),女,教授,博士,主要从事核地球物理、工程及应用地球物理方面的教学与研究工作,E-mail:jinghua@jlu.edu.cn。
