自组织竞争网络在测井资料岩性识别中的应用
2012-09-06丁洁
丁 洁
(忻州职业技术学院计算机系,山西忻州 034000)
自从1982年Wolf等人首次提出根据测井资料自动判定地层岩性以来,利用计算机自动进行岩性识别已成为测井技术和钻井技术发展的重要方向。目前,岩性识别主要有以下几种方法:(1)概率统计方法;(2)聚类分析方法;(3)人工神经网络方法。人工神经网络方法以其自身特有的样本学习能力获得识别模式[1],以与岩性相关的测井资料作为神经网络的输入参数,已知岩性种类作为输出总数。前两种数理统计方法,两者的差别只是参数选择的要求不同。人工神经网络具有很强的自组织性、自适应性、容错性和推理思维能力,人们运用神经网络在测井资料岩性识别领域做了大量的研究,取得良好效果[2]。
论文主要研究利用自组织竞争神经网络进行测井资料岩性识别的方法,概述了自组织竞争神经网络的基本原理以及测井资料岩性识别的步骤,在考虑岩性影响因子的基础上,对测井资料进行岩性识别。
1 自组织竞争神经网络原理
1.1 自组织竞争神经网络的结构
基本竞争型网络结构如图1所示。

图1 基本竞争型神经网络结构
由图1可知,自组织竞争神经网络包括输入层(输入测井数据信息)和竞争层(岩性分类模式)。上下层之间实现全连接,而每层神经元之间无连接。
1.2 自组织竞争神经网络学习规则
自组织竞争网络的学习规则以竞争型学习规则为主[3-5]。竞争型神经网络可分为输入层和竞争层,网络结构如图1所示,可以假定输入层由N个神经元构成,竞争层由M个神经元构成。网络的连接权值为wij,i=1,2,…,N,j=1,2,…,M,且满足约束条件wij=1。
竞争型网络的输入样本是二值向量,各元素取值0或1,竞争层神经元j的状态可按公式(1)计算。

公式(1)中xi为输入样本向量的第i个元素。根据竞争机制,竞争层中具有最大加权值的神经元k赢得竞争胜利,输出为:
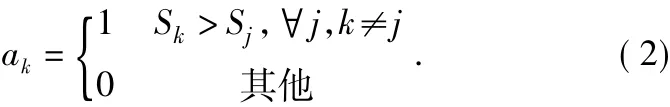
竞争后的权值按照公式(3)进行修正,对于所有的i,有:
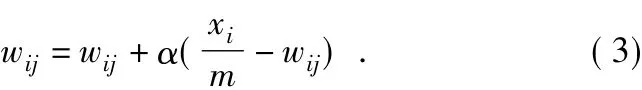
其中,α为学习参数,0<α<1,一般取为0.01~0.03;m为输入层中输出为1的神经元的个数,即m=Xi。权值公式项表示当x为1时,权值增加;而x当为0时,权值
ii减小。也就是说,当xi活跃时,对应的第i个权值就增加,否则就减小。由于所有权值的和为1,因此当第i个权值增加或者减少时,对应的其他权值就可能减小或增加。此外公式(3)还保证了权值的调整能够满足所有的权值调整量之和为0。
2 样本数据的获取
2.1 样本的选取
样本包括样本特征选取及样本数目的确定。样本特征应能很好地反映这类问题的基本特征,不仅在训练区内有代表性,而且在预测区内有普遍性。样本数目过少可能无法充分地反应网络性能,从而导致网络外推的能力不够;而样本过多可能出现样本的冗余,既增加了网络的训练负担,也有可能出现包含信息量过剩。总之,样本选取具有代表性的样本资料。按照这一原则,采用北方某地区2009年的测井资料进行研究,该地区属于碳酸盐地层,因此需要判断的岩性有三种,即泥岩、砂岩和石灰岩。通过对已知井段测井数据进行学习,来预测同一地区其他井段的岩性。
2.2 样本数据的预处理
样本准备工作是非常重要的环节,因为它直接影响网络的正确性和应用的可行性。取得的样本数据不能直接用作神经网络的输入,需要对测井数据进行归一化。将数据处理为区间[0,1]之间的数据。归一化方法可采用归一化公式:
式中:xi、ximax、ximin分别表示第i个测井数据及在样本中的最大、最小值,¯xi表示归一化后的测井数据。
测井资料的样本数据中包含了影响岩性的5个重要因子,即补偿中子空隙度CNL、补偿密度曲线DEN、声波时差DTC、自然伽玛GR和微电阻率RT。
归一化后的数据如表1所示。

表1 归一化后的岩性影响因子
测井数据的标准化使各类测井信息在研究区域内有一个统一的刻度标准,使可能影响原始测井数据的各种系统误差减至最小,以消除非地质因素造成的测井响应的井间差异。通过对测井数据的归一化,很大程度上减小了非地质因素导致的井间差异的影响。使学习样本集具有真实性、全面性和代表性。这是用神经网络解决好实际地质问题的关键。
3 测井岩性识别模型的建立
3.1 测井岩性识别算法
测井岩性识别流程图如图2所示。

图2 测井资料岩性识别流程图
图2给出了应用自组织竞争网络进行测井资料岩性识别的流程图。
3.2 自组织竞争神经网络结构设计
图2设计了一个基于自组织竞争神经网络的岩性识别模型,实现岩性分类首先选择一个适当的网络结构。论文选用自组织竞争网络的两种网络模型比较网络的性能。
自组织竞争网络的神经网络工具箱提供了大量的函数工具[3]。自组织竞争网络由输入层和竞争层组成。用newc函数创建一个竞争层,构建一个基本竞争型网络。权值函数为negdist,输入函数为netsum,初始化函数为midpoint或者initcon,训练函数或者自适应函数为 trains和trainr,学习函数为learnk或者learncon函数。函数返回值是一个新的竞争层。由于需要识别的类别数目是3,神经元数目也设置为3,为了加快学习速度,将学习速率设置为0.1。用newsom函数创建一个自组织特征映射网络。自组织特征映射网络的输入层中的每一个神经元,通过权与输出层中的每一个神经元相连。构成一个二维平面阵列或一个一维阵列。输入层和竞争层的神经元之间实现全互连接。利用基本竞争型网络进行分类,需要首先设定输入向量的类别总数,再由此确定神经元的个数。利用自组织竞争神经网络进行岩性识别,不必对输入的测井数据进行统计,只要将网络自动分类号与相应的岩性对应,即可实现自动岩性分类识别。
4 在MATLAB环境下实现测井资料岩性识别
4.1 测井资料岩性识别的MATLAB实现
(1)用newsom函数创建一个自组织特征映射进行岩性分类:
①建立网络
net=newsom(minmax(P),[6 5]);% 网络竞争层的神经元的组织结构6×5 plotsom(net.layers{1}.positions);%绘制神经元初始位置
title(’神经元位置的初始分布’)
figure;
运行结果如图3所示。
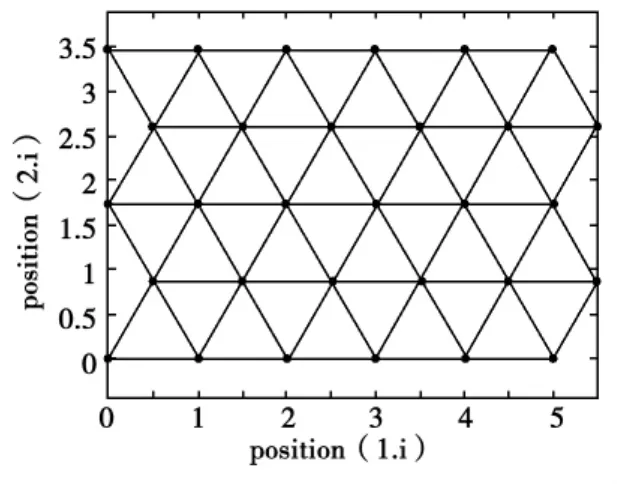
图3 神经元初始位置图
此时的神经元分布如图3所示,此时的神经元位置是均匀分布的,也就是说,网络还没有对输入向量进行分类的能力。
②测试
%对训练步数为10时测试网络性能
P_test=[0.7601 0.8123 0.8079 0.8450 0.8792]';
Y_test=sim(net,P_test)
Yc_test=vec2ind(Y_test)
运行结果:
Y_test=(1,1)1
Yc_test=1
分析结果表明该组数据为属于石灰岩。
③绘曲线图
%绘制训练后输入向量分布图
plot(P(1,:) ,P(2,:) ,'.r','markersize',20);
title('训练10次后输入向量分布')
figure;
运行结果如图4所示。
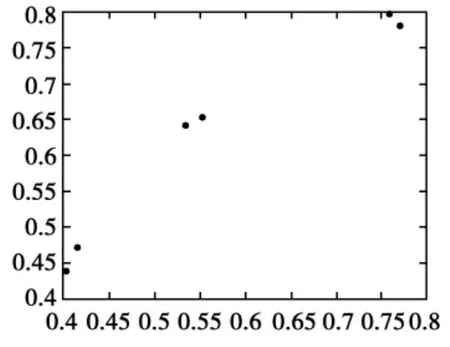
图4 训练10次后输入向量分布
图4显示,训练了10次后输入向量已经分类。
%绘制训练10次后岩性分类曲线
Plot(Yc);
title(’训练次数为10时岩性分类’)
figure;
运行结果如图5所示。

图5 训练10次后神经元分布
由图5可知,经过10次训练后,神经元的位置就发生了明显的改变,神经元位置的分布情况表示它们已经对输入向量进行分类了,此时再增加训练次数已经没有什么实际意义了。在实验中重新运行上面的代码时,结果可能不一致,因为每次激发的神经元不一样,但是相似的类激发的神经元是邻近的,差别很大的类激发的神经元相差较远。
5 结束语
论文主要研究了自组织竞争神经网络在测井资料岩性识别中的应用方法,介绍了自组织竞争神经网络的原理、应用步骤及在测井资料自动分层中的应用,采用了MATLAB工具进行网络的设计和处理。研究结果表明,采用自组织竞争网络与自组织特征映射网络进行测井资料岩性识别是可行的,识别率比较高。由于测井资料所携带的重要的地质信息可以确定地层含油储量,而且还是制订开采规划的重要依据,因此利用自组织竞争网络进行测井资料岩性识别具有很大的意义。
[1]陈祥光,裴旭东.人工神经网络技术及应用[M].北京:中国电力出版社,2003.
[2]高隽.人工神经网络原理及仿真实例[M].北京:机械工业出版社,2009.
[3]许东,吴铮.基于 MATLAB 6.x的系统分析与设计[M].西安:西安电子科技大学出版社,2003.
[4]王洪元.人工神经网络技术及其应用[M].北京:中国石化出版社,2008.
[5]王鸿斌,胡志军.人工神经网络理论及其应用[J].山西电子技术,2006(2):41-43.
