市政管线的综合布置及数学建模研究

杨 杰

(皖西学院 建筑与土木工程学院，安徽 六安 237012)

市政管线的综合布置及数学建模研究

杨 杰

(皖西学院 建筑与土木工程学院，安徽 六安 237012)

在探讨空间布局问题的基础上分析了管线布置系统中的各种约束因素，并提出约束关联网在综合布管中的应用;从管线布置的流量约束、路径约束、费用约束和空间约束着手，建立了一个多目标规划数学模型，并利用分层排序法对模型的最大流量函数、最短路径函数、最小费用函数和空间内互不干涉的最小剖面积函数进行求解。研究表明:管线系统数学建模具有一定的可操作性，为城市市政管网的定线提供了参考。

市政管线;综合布置;约束;多目标规划;数学模型

市政管线系统的综合布置属于空间布局问题的范畴，布局问题［1］是指在满足一定的限制条件下，根据布局空间的和待布物体的相互关系，将其合理地放置于空间中，并且符合问题的最优化要求。待布物体的不规则性与待布空间的不定性使布局问题变得复杂多变，国内外许多学者对其做了大量的研究，并取得了一定的成果。黄振东［2］等对带平衡约束的矩形布局问题，提出了一种新的混合算法来进行求解;梁勤欧［3］等对设备布局问题进行了相关研究，并通过免疫遗传算法来验证设备间的优化布置;Sweeney［4］等对布局空间与待布物体之间的关系进行了相关的分析和论述;Jain［5］等利用改进遗传算法，求解二维空间布局问题;Gent［6］将启发式算法应用于装箱布局问题中，并通过实际案例验证其最优化布置情况。然而，由于布局问题的复杂性以及各个领域的差异性，很难找到一种通用算法对所有布局问题进行求解。对于市政管线系统综合规划，本文从影响管线布局问题的各种限制性因素着手，分析了几种条件下的约束目标与约束条件，建立多目标规划数学模型，并寻求模型的解法，尝试性的探讨多种管线的空间布置问题。

1 管线综合布置的约束因素分析

1.1 约束的分类

在市政管线的综合布置中，对影响系统的各种限制性因素进行描述和分析是解决问题的切入点，此处的限制性因素即约束，如管道的尺寸、管径、流量等，它们在系统布置中起着一定的约束作用。可以说，一个布局问题的求解过程，也是一个对约束的处理过程。管线布置系统中的约束［7-8］类型可以分为以下几种:

1.1.1 管线顺序约束

指管线的放入顺序对管网布置空间所产生的约束。管线布局的顺序可以按照定序和定位进行分配，一个三维空间布局顺序约束为:按管线系统的容积递减;管线系统面积递减;管线系统长度、宽度和高度递减定序。

1.1.2 管线几何约束

即几何形状和尺寸对管线系统布置所形成的约束限制，具体可分为线性约束、平面约束以及空间约束;为了求解布局问题，有时可以通过调用几何形状和尺寸约束，将平面布局简化为线性布局。

1.1.3 管线位置约束

指各种管线之间以及管线与待布空间之间的相互限制，城市地下管线的位置约束主要表现为管线之间的垂直相间、平行相邻和斜相交等位置关系。

1.1.4 管线属性约束

指管线的流量、流速、压力损失、材料、强度等特定属性的对布管的影响。通过对布局管线各种设计属性的分析，一定程度上可确定其布局空间的最佳位置。

1.1.5 管线干涉约束

在管线系统空间布局中，各种因素是相互影响和制约的，如管线的几何尺寸对管线的放入顺序产生约束:先放大尺寸管线，后放小尺寸管线;但同时，各种管线自身的属性又影响其与相邻管线的定线，即特定的两种或多种管线之间存在位置上的干涉影响和约束。

1.2 约束关联网

在一个三维空间布局问题中，各种约束之间既相互联系又相互制约，形成一个或一系列的关系网络，称之为约束关联网。市政管线系统的空间布置可以通过组合多个管线约束，建立数学关系式，确立管线系统的约束关联网进行合理布管。如在均匀流管道中存在的约束变量有:流速 v，流量Q，管长，管径 d，雷诺数 Re，运动粘度系数，沿程阻力系数和水损hf。通过对这些约束变量的分析，其存在的数学关系式有:

管径、管长、流速、沿程阻力系数和水损关系式:

流量、流速和管径关系式:

管径、流速、雷诺数和流体的运动粘度系数关系式:

根据三个上述数学关系式，可建立起如图1所示的约束关联网。

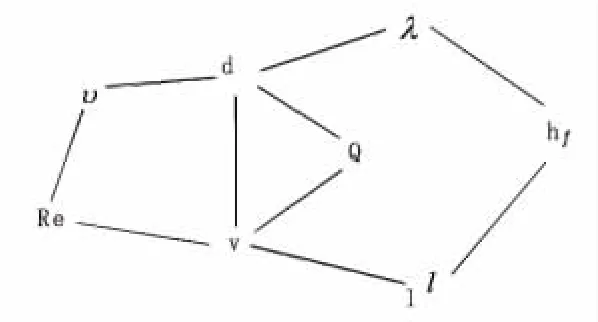
图1 均匀流管道中的约束关联网

对于多种管线的综合布置，涉及到的限制条件和约束因素很多，联立各个约束变量组建起多个独立的关系网，再利用其中的公共约束，建立起一系列相互联系的约束关联网;通过已知约束变量和公共约束变量的调用可求解其他未知约束变量，从而对管网综合布置方案进行优化设计。

2 市政管网布置系统数学建模

2.1 一般规定

在一个涉及复杂管线系统的城市综合管网中，定义:管网集 A=［N，M］，其中，N 为管网的节点集，N=［1，2，…，n］;M 为管网的管段集，J=［1，2，…，m］;管网中的管线种类记作 S，S=［1，2，…，s］。管线段可以表示为 k(i，j)，且起点集合 O=［o1，o2，…，om］，终点集合 T=［t1，t2，…，tm］，ok是管线k的起点，tk是管线 k的终点;起始于节点 i的管线记作:MOi=［k︳ok=i］，终止于节点 j的管线记作:MTj=［k︳tk=j］。

2.2 流量约束

在城市综合管网布置系统中，首先需要保证的是管网流量的连续性，即满足管网各节点的流量平衡，对于内部点，其流出量和流入量是相等的;对于始末点，其全部流量等于外部的净输出量;其次是满足管网容量的约束条件［9］，即管段上的流量不能超过始点与末点的需求流量。令管网的始点为a，末点为 b，则流量约束的数学模型可描述为:

式中:αks为第s种管线段k上损失系数;qks为第s种管线段k上的流量;vs为第s种管线始末点的外部流量;v0为第 s种管线始末点的需求流量。

2.3 路径约束

对于一个待布置的综合管网，管网中的任意两点可能都存在多条布管路径，从数学规划的角度出发，我们通常寻求的最佳路径是一条最短或最经济路径，即求一条权值最小的路径，同时该路径必须满足一定的约束限制;因此，在管网的路径约束中可以定义一个权值系数，当从节点 i到节点 j存在管线时定义为1，节点i到节点j之间不存在管线时则为0;此外，管网路径需要满足流向的约束限制［10］，管网布置的路径约束如下:

式中:aij为管线(i，j)的权值系数;

2.4 费用约束

管线布置在管网造价中占很大的比例，管网在敷设时既要考虑到管道的流量、管径、埋深和管材，还要考虑到施工处的地方系数和分类管线系数。管网的费用可由管线上的相关约束来描述，某种管线的单位敷设费用可以看成是流量q、管径D和埋深H的非线性函数;此外，管线上的流量需满足上、下限要求，即不能超过一定的容量。管网布置的费用约束为:

式中:cks为第s种管线段k的敷设费用;fks为第s种管线段k的费用函数;qks为第s种管线段k的流量;hks为第s种管线段k的流量上限;

2.5 空间约束

市政管网是一个三维空间的网络系统，各种管线的布置在一定程度上受到剖面空间的限制:一方面，管线布置形式、坡度、水平方向与垂直方向间距等都需要满足工程规范的要求;另一方面，在敷设管网的城市地下空间内，管线埋设深度太小，易遭地面荷载的破坏，其安全性无法得到保障;而埋设深度太大时又会增加管网的工程造价。因此，在进行市政管网综合布置时，既要从各种工程管线的技术规范着手，又要保证多种管线间不发生相互干涉［11］，经济布管。管网的空间约束为:

式中:A为管网空间剖面面积;int(·)为管网中某种管线集合的内部;Ft，Fs为第 t种管线和第 s种管线;dtsx为第 t和第s种管线的水平布置间距;dax为管线水平布置间距下限标准;dbx为管线水平布置间距上限标准;dtsy为第 t和第 s种管线的垂直布置间距;day为管线垂直布置间距下限标准;dby为管线垂直布置间距上限标准;Aa为单管线的最小剖面积;Ab为多管线的最大剖面积。

2.6 目标函数

在管网的规划时，我们的总体要求是工程技术可行，经济上合理。综合上述流量约束、路径约束、费用约束和空间约束四个关系式，管网布置模型的目标函数可描述为:最大流量函数z1;最短路径函数z2;最小费用函数z3和布管空间内互不干涉的最小剖面积函数z4，问题的数学模型如下:

式中:lijs为节点 i到 j的第 s种管线长;cks为第 s种管线段k单位敷设费用;lks为第 s种管线段k上的管长;

α、β为地方系数和分类管线系数;

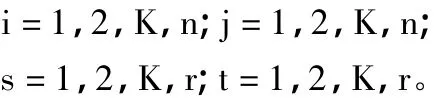
其他参数意义同上。

为实现多种管线空间布置的最优化问题，在约束变量满足给定的限制条件下，根据约束间的联系，列出上式的多目标规划模型:

则管网布置的目标函数又可以表示为:

3 模型求解

对于多目标规划问题的数学模型求解，通常的做法是将模型的多目标分解为为多个单目标，然后通过求解单目标的最优解最终实现多目标的优化问题。

分层排序法是一种常用的求解多目标规划问题的方法，该解法的基本思想［12］是:根据模型中各个目标函数对问题的影响和重要程度将其重新排序，求解第一重要级别目标函数;然后，在第一级目标函数的最优解集中，寻找第二重要级别目标函数的最优解集;如此往复向后一级推算，直到求解到最后一级别目标函数的最优解或近似最优解，此解即作为整个多目标规划问题的最优解。对于市政管网综合布置的多目标规划数学模型，涉及到流量和管长等多个自变量，这些自变量分别存在于多种不同时点上，约束范围也不同，通过约束关联网，可以将多个具有差异的约束变量及其函数最优解联系起来，建立起约束关系，从而为下一级单目标函数的求解提供取值范围。

管网布置系统的多目标规划数学模型用下式表示:

利用分层排序法对此规划模型进行求解，并将模型中的目标函数f1(x)、f2(x)、f3(x)和 f4(x)按流量约束、路径约束、费用约束和空间约束的重要程度进行排序，设第一重要级别目标函数f1(x)的最优解为f1*，则:

再在第一级函数最优解中求第二级目标的最优解，在求解的过程中，根据约束关联网，联立两个目标函数间的约束关系，寻求公共约束变量，同时，结合各个关联网自身的约束条件和已求解的值进行下一级函数的求解。f2(x)的最优解为:

同理可以求出f3(x)的最优解 f3*;f4(x)的最优解是联立前面三个函数的约束关联网和约束解求得的，设其值为f4*，问题的模型为:

在满足前面三级目标函数的约束限制下，求得第四个目标函数的最优解记作x*，则x*便是管网综合布置系统多目标规划模型的最优解;这里的x*可以是流量或管径等多个变量的最优值，这样便可实现对市政管线综合布置系统的多目标规划模型求解。

4 结论

城市地下是一个有限的资源空间，本文正是从如何有效的利用城市地下空间，更合理的规划布置城市综合管线这个问题着手研究，并得出如下结论:

1)影响管线系统空间布局问题的约束因素主要有:管线顺序约束、管线几何约束、管线位置约束、管线属性约束和管线干涉约束等。各种约束之间相互关联形成一系列的约束关联网，通过已知约束变量和公共约束变量可确定其他未知约束变量，从而有助于对布管方案的设计求解。

2)在对市政管线综合布置系统数学建模时，从管网布置的流量约束、路径约束、费用约束和空间约束方面考虑，构建了一个多目标规划数学模型，并利用分层排序法对布管模型进行求解。

3)文章给出了管网规划布置数学模型的解法，但如何结合具体的工程实践进行设计求解;此外，如何从数字化的角度对城市综合管网进行建库管理、查询和分析等，这些都有待于进一步的研究和探讨。

［1］Dowsland K A，Dowsland W B.Packing Problems［J］. European Journal of Operational Research，1992，(56):2-14.

［2］黄振东，肖人彬.求解带平衡约束矩形布局问题的混合算法［J］.华中科技大学学报(自然科学版).2011，3(39):98-99.

［3］梁勤欧，周晓艳.基于免疫遗传算法的设备布局问题研究［J］.武汉理工大学学报(信息与管理工程版).2011，4(33):643-646.

［4］Sweeney P E and Paternoster E R.Cutting and Packing Problems:A categorized，application-oriented research bibliography［J］. The Journal of Operational Research Society，1992，43(7):691-706.

［5］Jain S and Gea H C. Two-dimensional packing problems using genetic algorithms［J］. Engineering with Computers，1998，3(14):206-213.

［6］Gent I P. Heuristic Solution of Open Bin Packing Problems［J］.Journal of Heuristics，1997，4(3):299-304.

［7］王金敏，王玉新，查建中.布局问题约束的分类及表达［J］.计算机辅助设计与图形学学报.2000，12(5):349-354.

［8］曹斌，谭建荣，伊国栋.管线布局设计的约束因素分析及建模方法研究［J］.中国机械工程.2002，13(15):1318-1323.

［9］詹森(P.A)，巴恩斯(J.W)，孙东川.网络流规划［M］.北京:科学出版社.1988:97-98.

［10］郝光，张殿业，冯勋省.多目标最短路径模型及算法［J］.西南交通大学学报.2007，42(5):641-646.

［11］翟金刚，冯恩民，李振民等.带性能约束布局问题的不干涉遗传算法［J］.大连理工大学学报.1999，39(3):353-357.

［12］黄红选，韩继业.数学规划［M］.北京:清华大学出版社.2005:339-342.

TU990.3

B

1004-1184(2012)05-0155-03

2012-05-02

六安市定向委托皖西学院市级研究项目(2011LW005)

杨杰(1983-)，男，安徽合肥人，硕士，助教，主要研究方向为城市给排水工程与技术。