基于动态模糊神经网络的多余力矩抑制方法

倪志盛，王明彦

(哈尔滨工业大学电气工程及自动化学院，150001哈尔滨)

负载模拟是导弹自动驾驶仪半实物仿真中不可缺少的重要技术手段，其目的是为分析和研究自动驾驶仪的飞行控制性能和舵系统的动力性能来获取地面试验数据，在自动驾驶仪的研制和性能测试中起着重要的作用.多年来，负载模拟技术研究一直是航空航天领域的重要课题.多余力矩是影响负载模拟技术性能的核心技术问题，它直接影响到系统的加载精度及动态响应性能，另外系统还存在机械连接环节的间隙非线性问题和对不同测试对象的适应性问题.这些问题使得传统基于模型的控制策略的控制精度和动态性能很难满足要求，引入智能控制策略成为一种趋势.文献［1］提出通过采用补偿控制和迭代学习控制来消除多余力矩，从而使电动负载模拟系统得以实现.文献［2］提出一种神经元控制器，可实现转矩输出精确跟踪给定.文献［3－4］采用在非线性前馈校正基础上的模糊自适应控制策略消除系统的多余力矩，改善系统的动态品质.文献［5］利用键合图建模与仿真方法，针对多余力严重影响施力系统动态加载性能的特点，提出了基于CMAC神经网络的复合控制来提高加载系统的动态性能.本文采用的动态模糊神经网络，是一种无须领域的专家知识，对系统自动建模及抽取模糊规则的网络，且模糊神经网络结构动态变化的，其模糊规则在学习过程中逐渐增长而形成.从仿真结果可以看出，基本消除了多余力矩对加载系统的影响.

1 电动负载模拟系统与多余力矩问题

电动负载模拟器是一个位置扰动型的转矩伺服系统，由加载电机、PWM驱动装置、传感器以及控制器组成，它与舵机系统一同构成了完整的电动负载模拟系统，如图1所示.图中，承载电机(舵机)作为被加载对象与加载电机通过刚性轴直接相连.加载过程中，传感器采集相应的转矩、转角信号，通过信号调理电路和A/D转换进入控制器.控制器根据仿真计算机传输的指令，按照预先设计的算法输出控制信号，通过D/A转换传给PWM驱动装置，直接控制加载电机输出的转矩.

多余力矩是指当加载转矩给定为零时，由舵机转动而在轴上产生的转矩.图2为某一舵机的轴转角θ在－20°～20°变化时，多余力矩M达到近30N·m的实验波形.

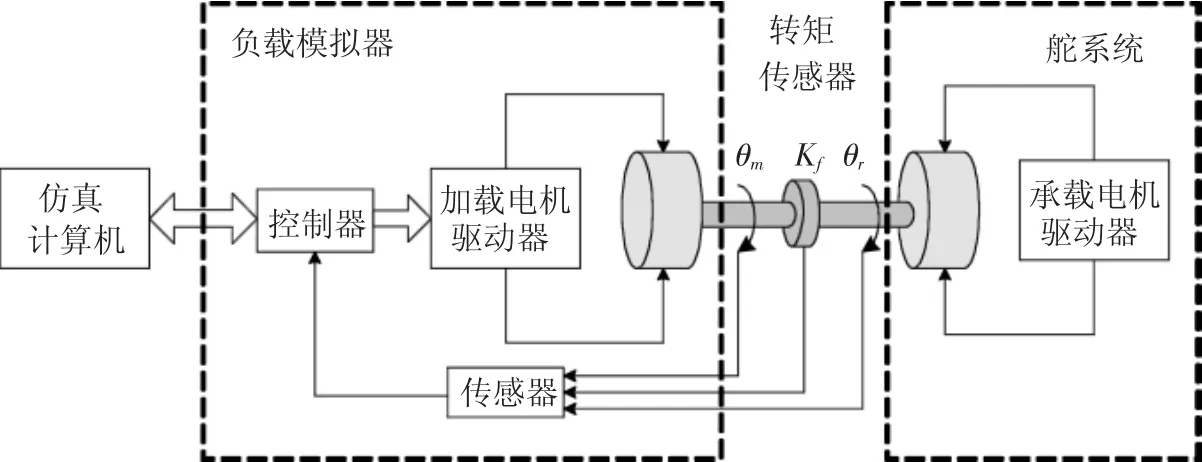
图1 电动负载模拟系统结构图

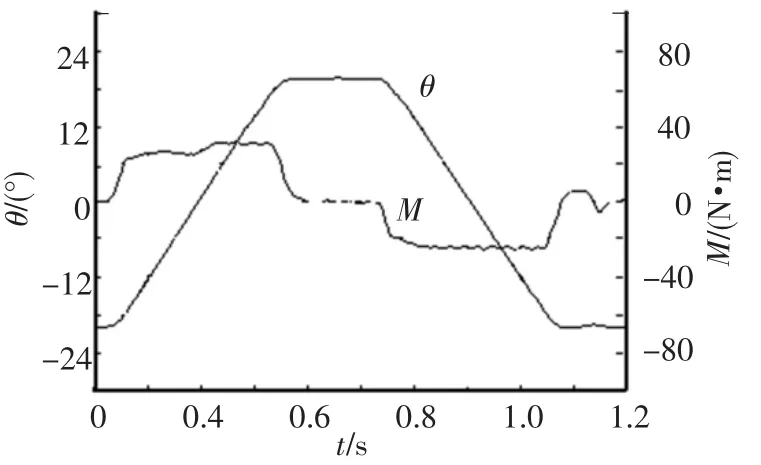
图2 多余力矩特性

多余力矩的产生与被加载对象的转动角速度以及角加速度等有关.加载电机与被加载舵机同轴连接，加载过程中，舵机主动跟随角位移指令作主动运动，加载电机则被动跟随舵机运动，同时对其进行加载，施加在轴上的转矩除指令加载转矩外，势必存在由于舵机运动而产生的多余力矩.由于舵系统的参数和运动形式的复杂性，多余力矩本身具有一定的不确定性，同时它也有较大强度，严重影响输出转矩的精度.多余力矩必然使得被动式力矩伺服系统与普通电力传动系统相比，在工作方式上具有本质上的不同，在很大程度上增加了系统控制难度.

2 动态模糊神经网络的结构和算法

本文采用的这种动态模糊神经网络的结构如图3所示，这种D－FNN结构［6］是基于扩展的径向基神经网络，在功能上等价于TSK模糊系统x1.图中，x1，x2，…，xr为输入的语言变量，y为系统的输出，MFij为第i个输入变量的第j个隶属函数，Rj为第j条模糊规则，Nj为第j个归一化节点，Wj为第j个规则的结果参数或连接权，u为系统总的规则数.第1层为输入层，每个节点分别表示1个输入的语言变量.第2层为隶属函数层，每个节点分别代表1个隶属函数，采用高斯函数表示，该隶属函数用高斯函数表示为

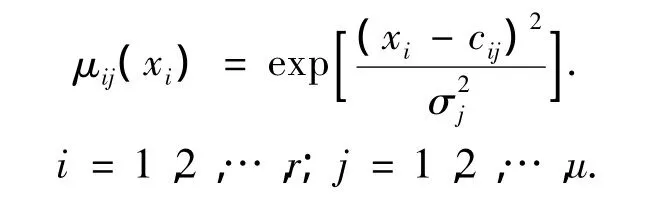
其中:μij为xi的第j个隶属函数，cij为第j个高斯隶属函数的中心，σj为xi第j个高斯隶属函数的宽度，r为输入变量数，u为隶属函数的数量，也代表系统总的规则数.

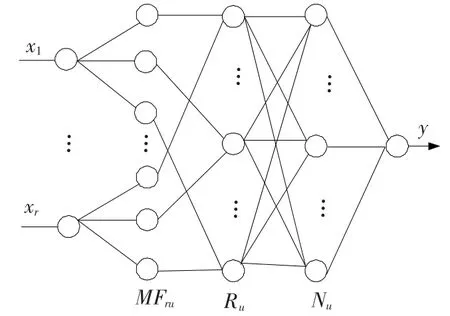
图3 模糊神经网络结构图

第3层为T-范数层，每个节点分别代表1个可能的模糊规则中的IF－部分，该层节点数反映了模糊规则数.第j个规则的Rj输出为

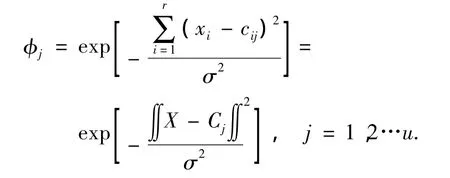
第4层为归一化层，N节点数和模糊规则节点数相等.第j个节点Nj的输出为

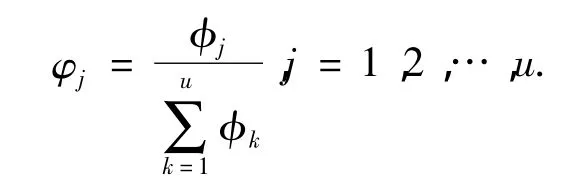
第5层为输出层，该层中每个节点表示1个输出变量，该输出是所有输入信号的叠加，即

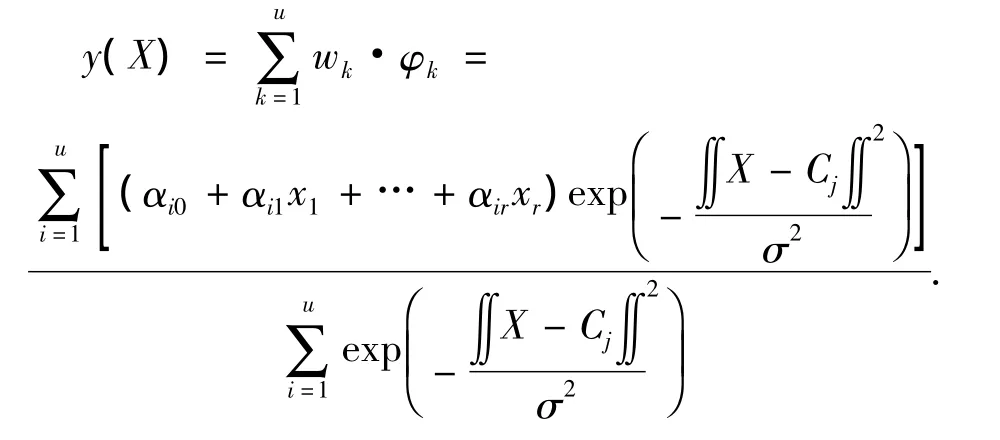
动态模糊神经网络的算法主要有6个部分组成:1)系统误差;2)可容纳边界;3)分级学习;4)前提参数分配;5)结论参数(权值)训练算法;6)修剪技术.算法流程图见图4.

系统误差判据.对于第i个观测数据(Xi，ti)，其中Xi是输入向量，ti是期望的输出，计算DFNN现有结构的全部输出yi.定义∬ei∬ =∬tiyi∬，如果∬ei∬ ＞ke，则要考虑增加1条新的规则，

这里ke的值是根据D－FNN期望的精度预先选定的.

可容纳边界判据.对于第i个观测数据(Xi，ti)，计算输入值xi和现有的RBF单元的中心Cj之间的距离di(j)，即di(j)=∬Xi-Cj∬，j=1，2，…，u，其中u为现有的模糊规则或者RBF单元的数量.找出dmin=argmin(di(j))，如果dmin＞kd，则以考虑增加1条新的模糊规则，否则，观测数据Xi可以由现有的最近的RBF单元表示，这里kd是可容纳边界的有效半径.

分级学习.每个RBF单元的可容纳边界不是固定的而是动态调节的.起初，可容纳的边界设置较大，以实现全局学习，随着不断学习，边界逐渐减少，开始局部学习.基于单调递减函数，逐渐减少每个RBF单元的有效半径和误差指数.也就是说，ke、kd不是常数，ke=max［emax×β，emin］，kd=max［dmax×γ，dmin］.其中 emax为预先定义好的最大误差，emin为期望的D－FNN精度，为收敛常数，dmax为输入空间的最大长度，dmin为所关心的最小长度，γ(0＜γ＜1)为衰减函数.

前提参数分配.新产生的规则的初始参数按照如下方式分配:Ci=Xi，σi=k×dmin，其中k(k＞1)是重叠因子.当第1个观测数据(X1，t1)得到后，此时的DFNN还没有建立起来，因此，这个数据将被选为第1条模糊规则:C1=X1，σ1=σ0.其中σ0为预先设定的常数.

结论参数(权值)训练算法本文采用梯度下降法.

修剪技术本文采用误差下降率法.ηi反映第i个规则的重要性ηi，当ηi值越大，表示第i个规则越重要.如果ηi＜kerr，则第i个规则可删除，其中kerr表示预设的阀值.

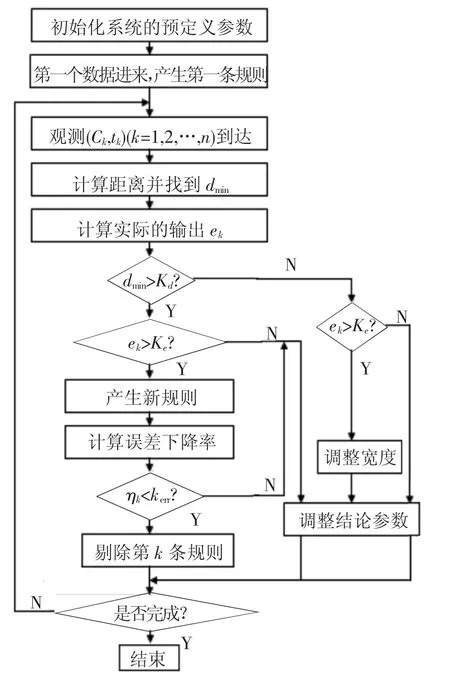
图4 D-FNN算法流程图

3 电动加载系统控制方案

针对电动加载系统的实际运行特点，考虑到其运行过程具有重复特性，仅有被加载对象频繁更换，而加载电机、轴系等环节始终保持不变，各种非线性因素也具有一定的相似性，因此，典型型号舵机的加载测试数据就成为重要的先验知识.电动加载系统在实际运行过程中往往是针对某个或某几个型号的舵机进行大批量的加载测试，同型号的不同被测对象的电气特性参数具有很大的相似性，这就决定了在测试同型号舵机的过程中，模糊神经网络辨识器和控制器的网络结构和参数会在很大程度上保持不变或者变化非常有限.虽然模糊神经网路的突出优势就是它优越的非线性逼近能力，但由于被控对象的参数仅在有限范围内作微小变动，不足以迫使已有的模糊神经网络结构和参数作大规模的变化和调整，所以在测试同型号舵系统的情况下，已获得的加载系统测试数据就成为重要的先验知识.但即使是同型号的舵系统，其不同批次、不同个体的电气特性参数也是服从一定的分布规律的，不可能完全一致，这就要求所设计的模糊神经网络的结构和参数要具有一定程度的在线修正和调整能力，以适应每个单独个体的测试需要.根据以上特点，设计了结合前馈反馈控制和直接逆控制的控制策略.该控制策略通过实时辨识负载模拟系统的逆模型，以产生补偿信号，控制系统中有两个动态模糊神经网络，如图5所示，D－FNN1用于系统的权值训练，D－FNN2则作为动态模糊神经网络补偿控制器，用来产生适当的补偿控制量.系统运行过程中，D－FNN1利用在线更新算法，实时更新网络结构及参数以及时跟踪被控对象逆模型的变化.

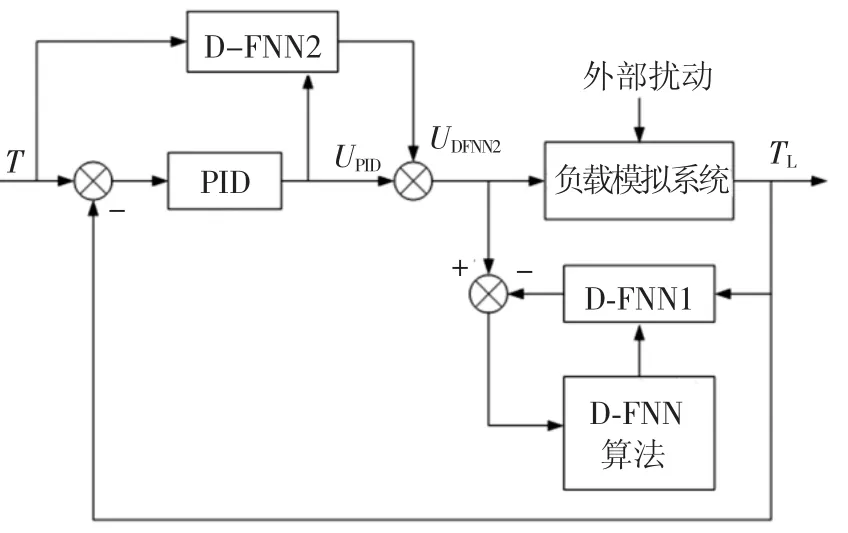
图5 D-FNN控制系统

D－FNN2是D－FNN1(已训练好的权值和结构)的直接拷贝，实时调整补偿控制量，当DFNN1逐渐逼近系统的逆模型后，D－FNN2将逐渐消除PID控制器的控制量UPID的作用，使得输出控制量UDFNN2=U，从而实现系统的输出TL跟踪输入指令信号T，最终实现系统的跟踪控制.虽然D－FNN2是D－FNN1的拷贝，但是它的权值会在控制器运行过程中作进一步调整，以补偿建模误差和未建模扰动.与其并行的PID控制器的作用在于保持系统的稳定并获得更快速的系统响应和更佳的跟踪精度.

4 仿真研究

根据本文提出的D－FNN控制策略，建立基于Matlab/Simulink环境下的系统仿真模型，并在不同的条件下对该控制策略的有效性进行仿真验证，仿真系统如图6所示.

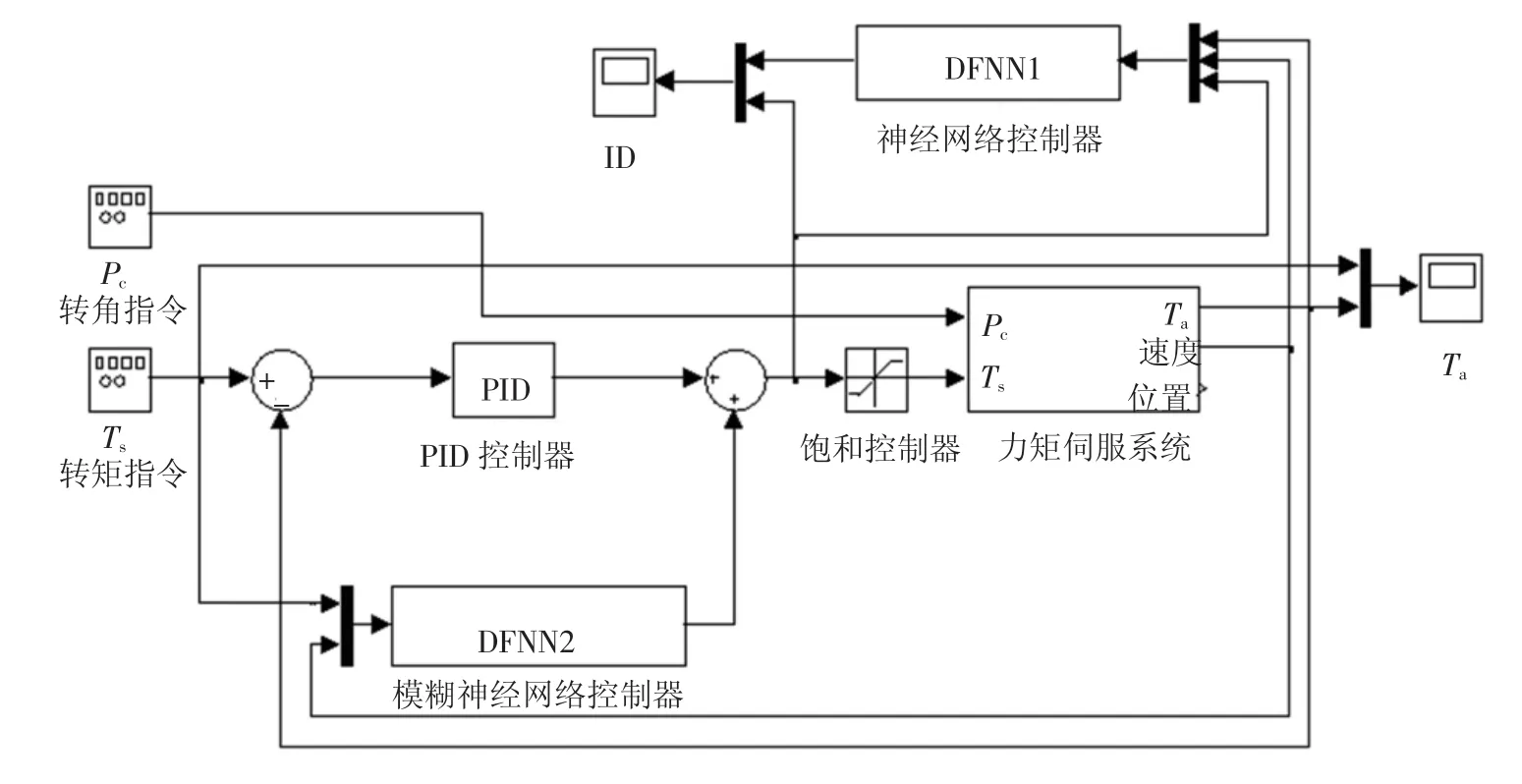
图6 Matlab/Simulink系统仿真模型

4.1 系统力矩伺服能力

以20Hz、80N·m正弦转矩指令信号作为系统激励，关闭图中的D－FNN1和D－FNN2控制器，此时，系统为一单位反馈闭环控制系统，仅有PID控制器在起作用.其转矩输出曲线如图7所示，可见此时的负载模拟系统转矩跟踪无论在幅值上还是在相位上都存在较大偏差，无法满足系统所要求的跟踪精度.打开D－FNN1和 DFNN2控制器D－FNN2控制器完全介入，与PID反馈控制器同时起作用，两个控制器输出的控制量之和为实际施加在被控对象上的控制量，如图8可见加入D－FNN2控制器控制量后，输出转矩曲线与指令转矩曲线已经基本重合，极大地缩小了幅值及相位偏差，系统的跟踪性能大大改善.图9给出了两种方式下转矩跟踪误差的变化情况，稳态情况下的误差峰值已经从32N·m减小到3.5N·m以下，转矩伺服精度大大提高.

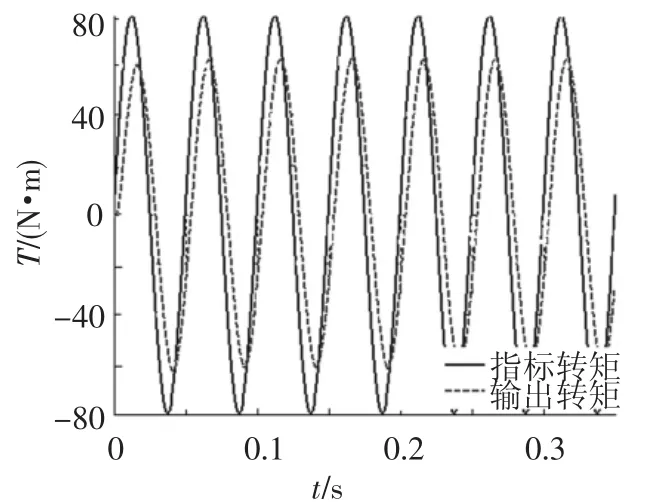
图7 PID控制下转矩跟踪

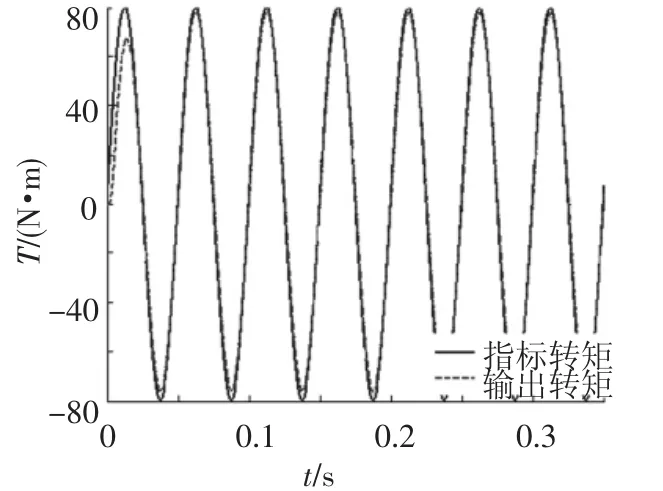
图8 D-FNN控制下转矩跟踪

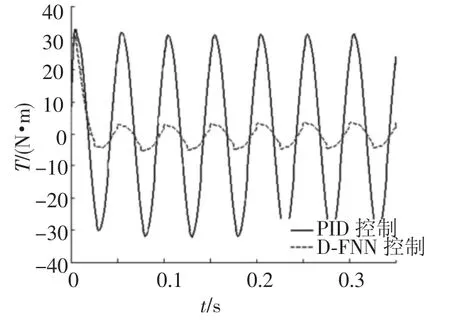
图9 两种控制方式下的转矩误差比较

4.2 多余力矩抑制能力

设定仿真转矩指令为0N·m，舵机转角指令为±2°，正弦波频率分别为5、10Hz.采用DFNN控制对模型对象进行仿真，轴上输出转矩如图10所示.

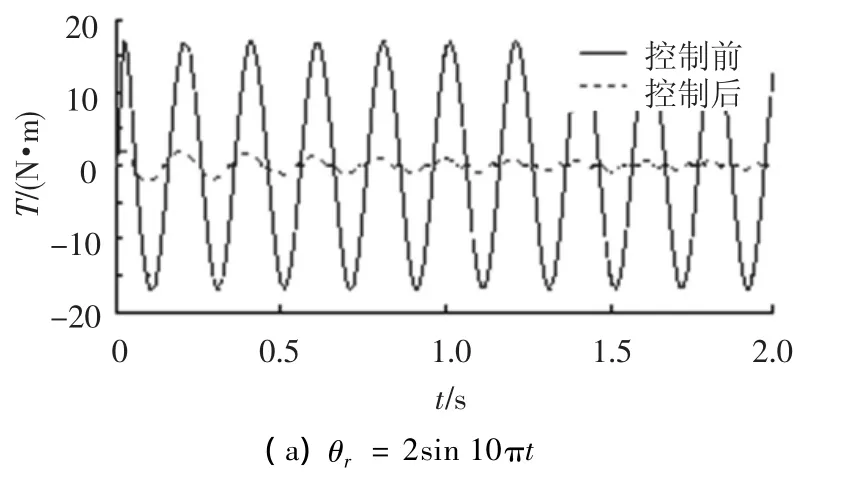
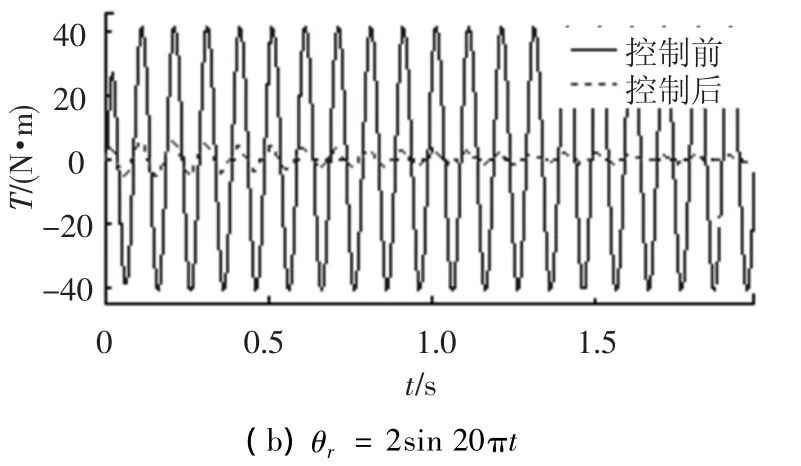
图10 DFNN控制下的多余力矩

由图10可见，在扰动为5Hz情况下，DFNN控制后的多余力矩约为0.5N·m;当扰动为10Hz情况下，多余力矩约为1N·m.两者消除多余力矩达到了97%，满足控制系统性能指标要求，显示了该控制策略良好的多余力矩抑制能力.

5 结论

1)电动负载模拟系统采用动态模糊神经网络，无须很强领域的专家知识，对系统自动建模及抽取模糊规则，能够对系统进行准确的辨识.

2)参数具有明确的物理意义，可根据经验选值，以便加快网络的收敛速度，给使用者带来了很大的方便.

3)结合前馈反馈控制和直接逆控制的复合控制策略，并联的PID控制器，有助于系统稳定和快速响应.

4)仿真显示该控制方案获得了很好的力矩伺服精度和抑制多余力矩的效果.

［1］王明彦.电动负载模拟技术的研究［D］.哈尔滨:哈尔滨工业大学，2004:29－34.

［2］罗雄飞，王明彦，刘畅.神经元控制器在电动负载模拟器中的应用［J］.控制工程，2007，14:39 －42.

［3］LIU C M，CHUEN C W，LEUNG T P.Fuzzy trajectory control of an electrohydraulic servo mechanism using binary weighted valves［J］.American Society of Mechanical Engineers，1995(2):15220.

［4］NAKAYANMA Y.Torque control method of three-inertia torsional system with backlash［C］//6th International Workshop On Advanced Motion Control.Nagoya，Japan:IEEE Conference Publications，2000:193 -198.

［5］叶正茂，李洪人.基于CMAC的船舶操舵系统负载模拟器复合控制［J］.工程设计学报，2002，9(3):147-150.

［6］WU S Q.Dynamic fuzzy neural networks:a novel approach to function approximation［J］.IEEE Trans，Man，Cybern:Part B，2000，30:358 －364.