铁路隧道内置隔墙的空气动力学分析及设计方法
2012-09-04贾永兴梅元贵
贾永兴,梅元贵
(兰州交通大学机电工程学院,兰州 730070)
1 概述
随着列车速度的不断提高,以及我国多条客运专线的投入运行,高速列车通过隧道时诱发的一系列空气动力学问题引起人们越来越多的关注[1]。隧道压力波问题因涉及到压力舒适性、车内环境及列车气密性等问题受到多方面的关注。就目前掌握的资料,国内外对高速列车通过单洞复线隧道或双洞单线隧道(通常设置横通道连接两隧道)引起的空气动力学问题的数值模拟分析已比较完善[2-7]。其中,基于一维可压缩非定常流动模型的特征线法分析结果准确、合理和经济,已成为高速铁路隧道设计中数值模拟压力波的主要方法。
1998年,在规划修建欧洲快速铁路网(Fast Train Network)时,曾出现过一种新颖的隧道结构形式——沿轨道方向设开孔隔墙,将单洞复线隧道变为“单洞单线”[8],以下简称为“内置开孔隔墙隧道”。内置隔墙隧道,即在单洞复线隧道内沿轨道铺着方向,在双线轨道中部加设纵向隔墙,将上下行铁路线隔开,形成2条与单洞单线隧道相似的隧道。国内外对开孔隔墙隧道内空气动力学方面的研究报道还比较少,目前仅见少量文献对该隧道新结构进行研究。文献[8]采用基于一维可压缩非定常等熵流动模型的THERMOTUN软件模拟单列车通过内置开孔隔墙隧道时的压力波变化情况,并与介质为空气1/175缩尺的动模型试验结果进行比对,验证了一维流动模型计算方法的正确性。文献[9]采用水介质模型试验方法研究了隔墙对压力波的恶化效果,但没有进行隔墙开孔对压力波减缓作用的研究。文献[10]介绍了兰州交通大学工业空气动力学研究中心对该方面的基础研究,该文在验证一维可压缩不等熵流动模型的特征线法在处理单列车通过内置开孔隔墙隧道时诱发压力波动问题的正确性的基础上,对一维流动模型的适用性进行了研究。
本文将首先对铁路隧道内内置开孔隔墙结构及其特点进行详细介绍。然后基于一维可压缩非定常不等熵流动模型建立流动控制方程。其后采用广义黎曼变量特征线法求解该控制方程,通过逆步进法构建求解网格系统对单车及两列车对向高速通过内置开孔隔墙铁路时诱发的压力波动问题进行求解。通过对典型隧道长度下该结构对隧道压力波特征的影响研究,在与现有舒适度标准对比分析后,为隧道断面设计提供空气动力学方面的依据。
2 铁路隧道内置开孔隔墙结构及其特点
连接荷兰与欧洲高速铁路网而修建的高速铁路线出于环境保护方面的考虑,线路在穿越“Groene Hart”自然保护区以及“Oude Mass”河、“Dordtsche Kil”河时均考虑修建隧道。同时该线路的设计方提出了设置开孔隔墙以及通风竖井等多种方案缓解高速列车隧道压力波的方案。图1所示为荷兰“Groene Hart”下内置开孔隔墙复线隧道的实拍图片。

图1 荷兰“绿色心脏”内置开孔隔墙隧道[11]
复线隧道内设置隔墙后,原单洞隧道被一分为二,每一侧隧道与单线单洞隧道形式类似。当列车在隧道内发生火灾等突发事故时,隔墙的另一侧隧道可以为人员的逃生和救援提供有利的空间。就此而言,内置开孔隔墙后在不增设其他设施的条件下,隧道的防火安全性相比普通的单洞双线隧道而言有极大的提升[12]。
除了在防火安全性方面的优势外,荷兰NLR模型试验、Thermotun/4数值模拟[8]以及兰州交通大学工业空气动力学研究中心对高速列车开孔隔墙复线隧道压力波的研究[10]均表明,与未设置开孔相比,隔墙上的开孔可减缓列车通过一侧隧道内的压力波动,减缓因设置隔墙增大了阻塞比而加剧的压力波动。这是因为隔墙开孔后,原来受到隔墙限制的空气流动可以通过开孔进行流动,且隔墙两侧的流动空间内的气流将建立联系。由此引起的流动也将更加复杂,因此有必要单独对此类结构对隧道压力波的影响进行研究。
3 理论方法介绍
本节首先基于一维可压缩非定常不等熵紊流流动模型建立流动控制方程。其后对求解该方程的方法——广义黎曼变量特征线法及逆步进法构建求解网格系统进行简要介绍。
一般而言,隧道横断面水力直径远小于隧道长度。因此,可将隧道内空气沿着径向的流动忽略,而将三维流动简化为一维流动。简化的依据及合理性详见文献[1]。依据质量守恒、动量守恒及能量守恒定律,建立基本方程如下[1]。
连续性方程

动量方程

能量方程

式中,u、p、ρ、a、κ、F、˙m、t和x分别为流速、压力、密度、声速、比热比、隧道有效流通截面积、质量传递项、时间和距离。在隧道内不同流动空间中,上述方程中的摩擦项G、传热项q、列车壁摩擦功项ξ的具体表达式详见文献[1]所述。
由于隔墙开孔两侧存在压差,将引起隔墙开孔处的气体流动及隔墙两侧隧道内的传质现象。公式(1)、(2)及(3)中,隔墙开孔处的质量流量˙m为[10]

式中:α为开孔的流量系数;A为开孔面积;Δp为开孔两侧的空气压力差。其余在数值计算中需要考虑的初始条件及边界条件的处理详见文献[1]。
本文采用广义黎曼变量特征线法求解方程(1)~(3)构成的一阶拟线性双曲型偏微分方程组。限于篇幅,广义黎曼变量特征线法、数值模拟中使用的网格系统及程序的正确性等问题参见文献[1,10],此处不再过多叙述。
4 数值模拟结果
采用文献[8]中的列车模型几何参数对单车及两列车对向通过内置开孔隔墙隧道时诱发的隧道压力波进行模拟。其隔墙开孔的直径为0.72 m,开孔间距设置为25 m。列车速度为250 km/h。其余计算参数如表1所示。
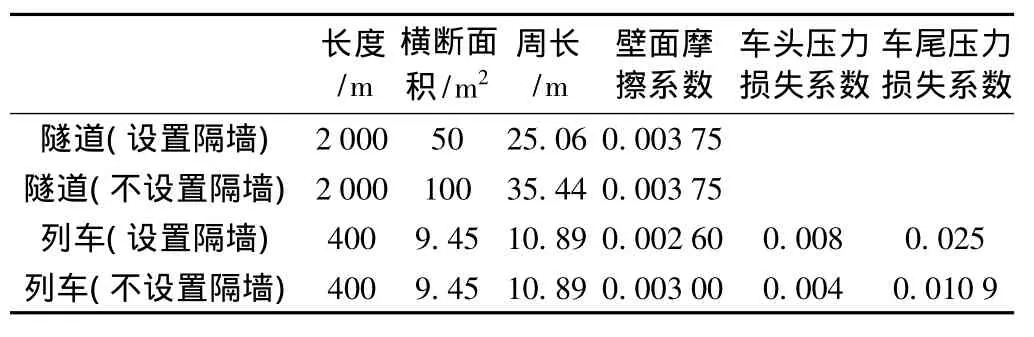
表1 计算参数
通过前述数学模型及求解方法,先后建立了单车通过内置开孔隔墙隧道程序及两列车对向通过内置开孔隔墙隧道程序。后期的工作中实现了两程序的统一,可使用两列车对向通过内置开孔隔墙隧道程序实现表2中除工况D外其余工况数值模拟。本节研究3种隧道形式(不设置隔墙,设置不开孔隔墙及设置开孔隔墙)及2种行车模式(单车及会车(本文仅考虑中央会车情形))下,共6种计算工况下隧道内的压力波。
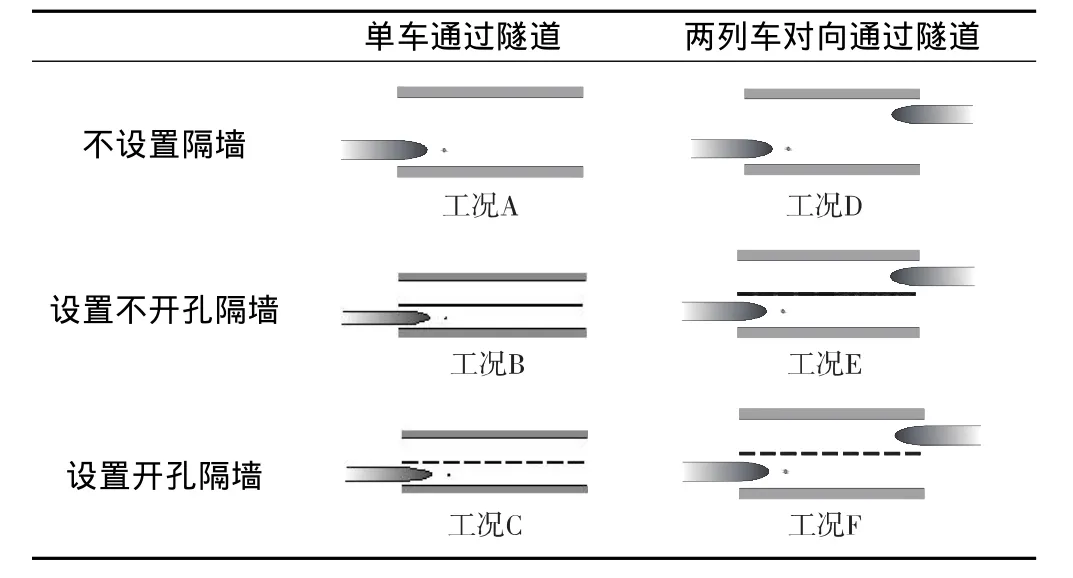
表2 计算工况
4.1 单列车通过内置隔墙隧道
单车通过隧道时,即表2中工况A、工况B和工况C,距离隧道入口500 m及1 000 m处列车通过一侧压力波动时间历程如图2所示。各种工况中,压力波动的趋势保持一致。由于工况B设置不开孔隔墙,隧道横断面积相比工况A减小一半,压力波动峰值与不设置隔墙时明显增大。而工况C由于设置开孔隔墙,隔墙开孔将工况B中两侧隧道的流动区域建立了联系。流动空间的增大使得压力波动相比设置不开孔隔墙的隧道内压力波动有所减弱,但由于开孔的全部面积小于不设置隔墙时完全连接的流动区域,工况B中压力波动大于工况A。

图2 单列车通过不同形式隧道时隧道内压力波动时间历程
图3所示为单列车通过不同形式隧道时,车头及车尾外侧静压波动的时间历程。与图2类似,隧道断面积最大的工况A,车外压力波动最平缓;而单侧隧道横断面积最小且隔墙不开孔的工况B,车外压力波动最为剧烈。而工况C,单侧隧道横断面积隧道为工况A的一半,但由于设置开孔的原因,车外压力波动有所缓减。在求得车外压力波动后,通过气密指数方法可以确定车内压力波动情况及3 s内最大压力变化情况。如图4和图5所示为气密指数15 s的高速列车通过不同形式隧道时车内压力波动时间历程及车内3 s最大压力变化量。容易得到与图2和图3类似的结论,隧道内置开孔隔墙情况下,如采用气密性能良好的高速列车,其车内压力舒适度水平基本与隧道内不设置隔墙的单洞双线隧道内的压力舒适度水平相当。根据国内客运专线舒适度阈值的建议(2006年),气密指数为15 s的单列高速列车通过本文所述类型的隧道时,其车内3 s最大压力变化量均小于该建议文件中线路类型D规定的阈值——山丘复线隧道(隧线比大于25%或隧道密集程度>4座/h),其最大压力变化量1.25 kPa/3 s。

图3 单列车通过不同形式隧道时车外压力波动时间历程

图4 单列车通过不同形式隧道时车内压力波动时间历程
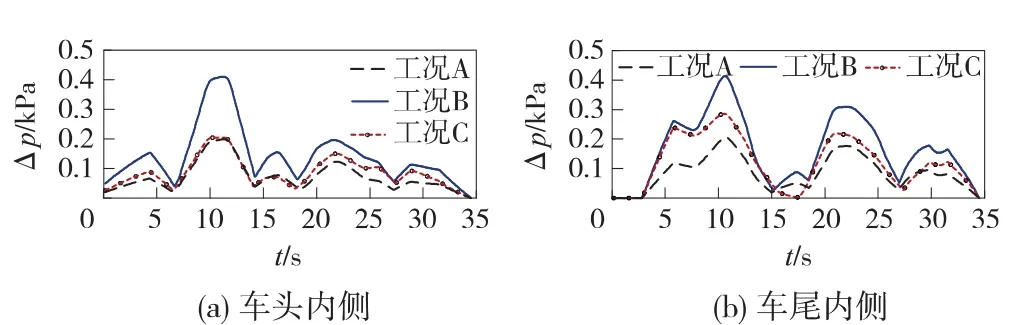
图5 单列车通过不同形式隧道时车内不同位置3 s内压力最大变化量
4.2 两列车对向通过内置隔墙隧道
两列车对向通过隧道且在隧道中央处交会时,即表2中工况D、工况E和工况F,距离隧道入口500 m及1 000 m处压力波动时间历程如图6所示。此时,隧道内压力变化情况比较复杂,其压力波动的趋势不仅与隧道结构有关也与观测点位置有关。工况E设置了不开孔的隔墙,由于隔墙将隧道隔离为两个完全独立的流动空间,两对向列车通过时与单车通过时引起的压力波动情况完全一致。由于开孔隔墙两侧隧道流动空间流动的相互影响,距离隧道入口500 m处观测点观测到的压力波动比其余两种工况会车更剧烈;而在该类隧道结构中距离隧道入口1 000 m处观测点观测到的压力波动与其余两类隧道结构中观测到的压力波动趋势基本相当,但局部峰值是3种模拟工况中最大。开孔隔墙结构使隧道内压力波动更加剧烈。

图6 两列车对向通过不同形式隧道时隧道内压力波动时间历程(中央会车)
图7所示为两列车对向通过不同形式隧道时,车头及车尾外侧静压波动的时间历程。与图6类似,隧道断面及最大的工况D,车外压力波动最平缓;而单侧隧道横断面积最小且隔墙开孔的工况F,车外压力波动最为剧烈。两列车对向通过设置不同隔墙的隧道时,开孔隔墙隧道内两侧隧道流动空间流动的影响使得工况F压力波动最为剧烈。

图7 两列车对向通过不同形式隧道时车外压力波动时间历程(中央会车)

图8 两列车对向通过不同形式隧道时车内压力波动时间历程(中央会车)
与单列车通过隧道情形类似,在求得车外压力波动后,通过气密指数方法可以确定车内压力波动情况及3 s内最大压力变化情况。如图8和图9所示为气密指数15 s的高速列车通过不同形式隧道时车内压力波动时间历程及车内3 s最大压力变化量。可以发现,两列车对向通过设置隔墙隧道时,不论隔墙是否开孔,其压力舒适度水平基本相当,且舒适度均小于不设置隔墙的情况。对于本文所模拟的工况,气密指数为15 s的单列高速列车通过隧道本文所述类型的隧道时,其车内3 s最大压力变化量均小于线路类型D规定的阀值。

图9 两列车对向通过不同形式隧道时车内不同位置3 s内压力最大变化量(中央会车)
5 结论
本文所述方法和程序可用于隧道内置隔墙类型隧道内压力波及车内压力波动的数值模拟。对于内置开孔隔墙的铁路隧道,列车以250 km/h运行时,内置开孔隔墙隧道可有效缓减单列车通过该类型隧道时的车内外压力波动峰值。而对于两对向列车通过的情形,内置开孔隔墙结构对压力波动的缓减作用不明显。若采用本文所研究的气密指数15 s的高速列车,内置开孔隔墙结构隧道内压力舒适度满足国内客运专线舒适度阈值要求。
[1]梅元贵,周朝晖,许建林.高速铁路隧道空气动力学[M].北京:科学出版社,2009.
[2]Ahmed S R,Gawthorpe R G.Aerodynamics of road and rail vechiles[J].Vehicle System Dynamics,1985(14):319-392.
[3]R S Raghunathan,H.D.Kim T.Setoguchi Aerodynamics of high-speed railway train [J].Progress in Aerospace Sciences,2002(38):469-514.
[4]骆建军,高波,王梦恕.高速列车突入隧道时的三维非定常流的数值模拟[J].中国铁道科学,2005,26(1):16-19.
[5]田红旗.列车空气动力学[M].北京:中国铁道出版社,2006.
[6]梅元贵,赵海恒,刘应清.高速铁路隧道压力波数值分析[J].西南交通大学学报,1995(6):667-672.
[7]王磊,万晓艳,余南阳.隧道单车压力波数值模拟验证研究[J].土木工程学报,2006(12):104-107.
[8]E.A.Demmenie,A.C.de Bruin,E.Klaver.Experimental pressure wave research at NLR for high-speed rail tunnels.NTRTP-98375.
[9]徐一民,王韦,许唯临,刘善均,吴明军.高速列车对复杂隧道内空气压力的影响[J].四川大学学报:工程科学,2009,40(1):21-25.
[10]梅元贵,贾永兴,刘杨.内置开孔隔墙的高速铁路隧道压力波数值模拟方法[J].空气动力学学报,2011,29(6):789-794.
[11]Delft Cluster http://www.delftcluster.nl/website/EN/page749.asp
[12]铁道部工程设计鉴定中心.高速铁路隧道[M].北京:中国铁道出版社,2006.
