基于距离和时间的物流运输路线优化分析
2012-09-04南超兰武汉职业技术学院湖北武汉430074NANChaolanWuhanPolytechnicWuhan430074China
南超兰(武汉职业技术学院,湖北 武汉 430074)NAN Chao-lan (Wuhan Polytechnic,Wuhan 430074,China)
面对油价的不断上涨,物流运输企业的成本也在不断增加,如何应对这种挑战?物流运输企业的普遍做法是:强化经营管理,降本减耗,抵御风险。其中重要的一条就是不断优化运输路线,提高运输效率,降低运输成本。
物流运输是整个物流系统中重要的一环,是完成货物位移、产生空间效益和时间效益的过程。在满足货运要求的前提下,如何选择运输路线是非常重要的。物流运输路线优化的目的在于保障运输安全的前提下,使运输路线和运输时间达到最优,从而实现 “第三利润”。
在以往介绍的运输路线优化的方案中,往往只考虑一种影响因素,即距离或时间。如,“单纯的最短路线”方法,仅仅考虑距离的远近,并未考虑各条线路的运行质量,不能说明穿越网络的最短时间。因此,对运行时间和距离都设定权数就可以得出比较具有实际意义的线路。本文同时考虑运行距离和时间,以单一起点、单一终点的物流运输路线为例,来探讨物流运输路线优化问题。
1 设置问题
如图1所示是路路顺物流公司签订的一项公路运输合同,要将一批药品从A城送到H城,路路顺物流公司根据这两个城市之间的行车线路绘制了一幅公路网络图。其中A点是装货地,H点是卸货地,B、C、D、E、F、G是途中可能经过的城市。从A~H有多种路线可选择,如何选择最优路线?
2 传统的路线优化方法
2.1 单纯的最短路线法

单纯的最短路线法是以最短运行距离作为运输路线优化的目标。
起讫点不同的单一问题,可以这样来思考:初始,除了装货地和卸货地外,所有的节点都可以被认为是未解的点,始发点作为已解的点,通过多次迭代,依次找出始发点到达该点,乃至终点的最短路径。计算从始发点开始,具体步骤如下:
步骤一:求A~B的最短路径。
与B点直接相连的分别是点A、C。
即可行路线有: A→B (60); A→C→B (144); A→D→C→B (360)。
因此,最短路径取A→B(60)。B点已解。
步骤二:求A~C的最短路径。
与C点直接相连的分别是点A、B、D。
即可行路线有:A→C (108); A→B→C (96); A→D→C (324)。
因此,最短路径取A→B→C(96)。C点已解。
步骤三:求A~D的最短路径。
与D点直接相连的分别是点A、C。
即可行路线有: A→D (218); A→B→C→D (202)。
因此,取A→B→C→D (202)。D点已解。
步骤四:求A~E的最短路径。
与E点直接相连的分别是点B、F。
即可行路线有: A→B→E (114); A→B→C→F→E (246); A→B→C→D→G→F→E (462) 因此, 取 A→B→E (114)。 E点已解。
步骤五:求A~F的最短路径。
与F点直接相连的分别是点E、C、G。
即可行路线有: A→B→E→F (204); A→B→C→F (156); A→B→C→D→G→F (372)。
因此,取A→B→C→F (156)。F点已解。
步骤六:求A~G的最短路径。
与G点直接相连的分别是点F、D。
即可行路线有 A→B→C→F→G (258);A→B→C→D→G (270)。
因此,取A→B→C→F→G (258)。G点已解。
步骤七:求A~H的最短路径。
与H点直接相连的分别是E、F、G。
即可行路线有 A→B→E→H (210); A→B→C→F→H (252); A→B→C→F→G→H (378)。
因此,取A→B→E→H (210)。
故,A~H的最短路径为210公里,最优运输路线为:A→B→E→H。见图1粗黑线所示。
2.2 单纯的最短时间法
单纯的最短时间法是以最短运行时间作为运输路线优化的目标。
图2所示是装货地A到卸货地H,以及途中可能经过的城市B、C、D、E、F、G所运行的时间。
解题思路与最短路线法相同,这里就不再介绍解题思路。
按照多次迭代、依次寻找最短时间的解题思路,可知最短运行时间为108分钟,行走路线为:A→C→F→H。见图2粗黑线所示。
从上面的解题结果可知,优化目标不一样,所选择的运行线路会有所不同。单纯的最短运输路线,并未考虑各条线路的运行质量,如路况、交通拥挤等因素,不能说明穿越网络的时间最短。因此,同时考虑运行时间和距离,并对运行时间和距离都设定权数才可以得出比较具有实际意义的线路。

3 具有实际意义的路线优化方法——基于距离和时间加权的组合优化运输路线
3.1 重新确定两点间数值
3.1.1 分配权数
当多种因素影响物流运输的时候,依各影响因素的重要程度依次分配权重。如果重点考虑运输成本,同时也考虑运输时间,则可以将距离的权数设置较大数字,而时间设置较小权数。在这里,置距离权数设为0.6,时间权数设为0.4。
3.1.2 计算加权组合数值
距离和时间的权数设定后,则可以计算出两点间的加权组合数值,如表1所示。

表1 基于运行距离和运行时间的综合数值表
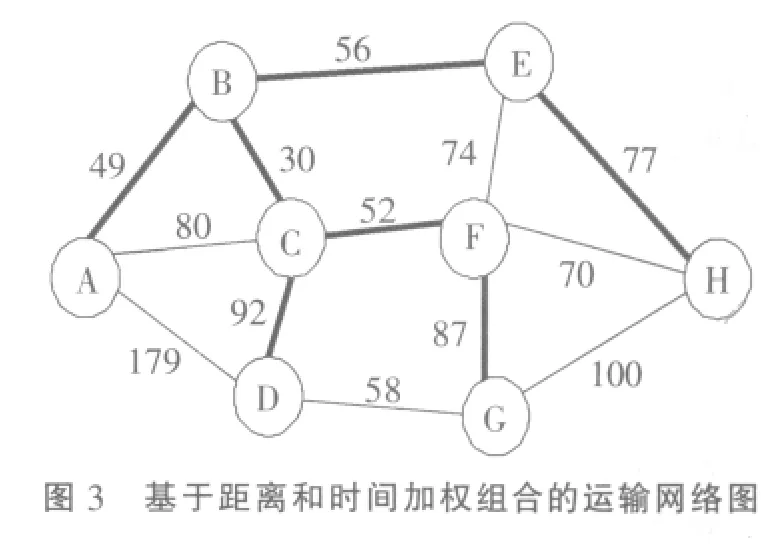
3.1.3 基于距离和时间加权组合的运输网络图
将加权组合数值在运输网络图上进行标注,如图3所示。则可以按照最短路线法的解题思路来规划最优的运输路线。
3.2 确定最优的运输路线
前面已经介绍了单纯的最短路线法的解题思路,此方法同样适用于基于距离和时间加权组合的线路优化问题。这里也不再重复。依据上述解题方法,我们可以知道最优运输线路为:A→B→E→H,见图3粗黑线所示。这种优化方案兼顾了距离最近和时间最短两种影响因素,是一种比较合理、更具现实意义的优化方法。
4 结束语
在运输路线优化问题处理时,可以依据实际情况进行调整。有的物流运输企业只考虑运输成本,可以运用单纯的最短路线法;只考虑最短运输时间,可以运用单纯的最短时间法。在实际运用中,一个理智的企业往往会考虑各种影响因素,这就需要用多种因素加权组合的方法来进行运输路线的优化。企业考虑的影响因素有非常重要、重要、次重要、不太重要等划分。企业可以根据自己的需要,调整不同因素的权数,然后作出决策,以反映企业优化运输路线时的评价标准。这篇文章只介绍了基于距离和时间的优化问题,如果考虑多种影响因素,也可以对多种因素设定权数的方法来解决。
[1]朱仕兄.物流运输管理实务[M].北京:北京交通大学出版社,2010.
[2]曲昭仲.物流运输管理与实务[M].北京:机械工业出版社,2009.
[3]匡水发,席波,周蓉.按高职教育规律培养适用物流人才[J].物流科技,2009(9):134-136.
