有里程和软时间窗约束的开放式多车场集送货一体化车辆路径问题研究
2012-09-04王明阳张丽华沈阳师范大学辽宁沈阳110034
陈 鑫,王明阳,张丽华(沈阳师范大学,辽宁 沈阳 110034)
CHEN Xin,WANG Ming-yang,ZHANG Li-hua (Shenyang Normal University,Shenyang 110034,China)
车辆路径问题 (Vehicle Routing Problem,VRP)最早是于1959年由Dantzig和Ramser[1]提出的,由于VRP的实用性与复杂性,VRP一经提出就引起了学术界广泛的讨论与研究。集送货一体化车辆路径问题 (Pickup and Delivery Vehicle Routing Problem,PDVRP)是对传统的VRP一个扩展,目前越来越受到关注。1983年和1988年Bodin等人[2]以及Desrosiers等人[3]就已经对满载集送货一体化车辆路径问题进行了研究。Savelsbergh M.W.P.等人[4]在1995年对集送货一体化车辆路径问题建立了数学模型,并对其特点、解决方案等进行了综述。对于非满载集送货一体化车辆路径问题,由于需要考虑到集货点先于送货点访问的问题,难度较大。2008年Sophie N.P.等人[5-6]对于集送货一体化问题进行了具体的分类。Li H.B.,Lim A.[7]和Gutiérrez-Jarpa G.等 人[8],Gambardella L.M.,Dorigo M.[9],Lu Q.,Dessouky M.M.[10],Dumitrescu I.等 人[11],Renaud J.等 人[12-13]对该问题进行了研究,并取得一定进展。
相较于国外,在国内,李军、郭辉煌[14]在其书中提到该问题,并给出了数学模型,并运用C-W节约算法对该问题进行了求解。霍振华、王新华[15],王兆庚、李建庚、程世东[16],屈援、汪波、钟石泉[17],钟石泉、贺国光[18]对带有时间窗约束的集送货一体化车辆路径问题进行了扩展,并对其进行了求解。霍佳震、张磊[19]对集送货一体化问题进行了进一步扩展,不再限制每项任务只有一个集货点和一个送货点,而是每项任务必须有一个集货点和一个或多个送货点,并对此问题运用修正的C-W算法进行了求解。相较于单车场集送货一体化问题,李臻、雷定猷[20],钟石泉、王雪莲[21]则将单车场扩展为多车场,对此类集送货一体化问题建立了数学模型,并通过表上作业法、遗传算法给出了问题的解。本文将前面文献中研究的集送货一体化车辆路径问题进行了扩展,即将单车场情形推广到多车场,将每个任务只有一个送货点推广到任务可以有多个送货点的情形,如此一来,前人文献中的算法不适用于求解本文的问题,因此本文给出一个遗传算法对其进行求解。
1 问题描述
由多车场发车执行货运任务的开放式带有里程约束的软时间窗集送货一体化车辆路径问题,可描述为:某物流公司有l项货运任务,表示为1,…,l,第i(i= 1,…,l)项任务均由1个集货点与hi(hi≥1)个送货点组成,这些货运任务由m个车场出发的同一种车型的车辆完成,每个集货点、送货点均有各自的时间窗限制,且若以[ET,LT]表示每个集货点、送货点的时间窗限制,则ET表示车辆到达该点的最早时间,后文称时间窗上限,LT表示车辆到达该点的最晚时间,后文称时间窗下限。已知每项货运任务的货运量为gi,车辆容量为q,并且满足q 本文中的每一条染色体都是所有任务的一个排序。 设种群规模为n(n为偶数)。 step1 将各个任务中的送货点按照时间窗进行排序,即将时间窗下限小的排在前面,如果时间窗下限相同,则比较时间窗上限,时间窗上限小的排在前面; step2 保持step1中各个的任务送货点的排序不变,将所有任务编号为1,2,…,l,按该编号得到所有任务的一个排序,即为一个染色体; step3 仍然保持step1中各个的任务送货点的排序不变,随机生成1,2,…,l的n-1个互不相同的排列 (这n-1个排列都与1,2,…,l的自然排列不同),分别按这n-1个排列生成所有任务的n-1个不同的排序,即得n-1条互不相同的染色体。 要确定每条染色体的适应值,首先要将该染色体改变成问题的一个解 (即在任务之间选适当的位置插入车场),之后计算该解的目标函数值z,取1/z为该染色体的适应值即可。 2.3.1 将染色体修改成问题的解 用 i(i= 1,…,l)表示第i个任务,那么如果i1i2…il是1,2,…,l的一个排列,则i1i2…il就表示一个染色体,用j(j= 1,…,m)表示第j个车场,下面将该染色体修改成问题的一个解。 计算各车场与第一个任务i1的集货点间的最小距离,设di1,j1=min{ di1,j|j=1,…,m},在任务i1前插入车场j1,让车辆从第j1个车场出发沿着i1i2…il的顺序前进 (其中各个任务的集货点及送货点的顺序已经排好),若该车辆在刚好完成第ik项任务时,行驶距离达到最大里程 (即完成第ik项任务时该车总的行程小于或等于最大里程,但若再完成第ik+1项任务时,总的行程就会超出最大里程),将任务i1i2…ik交由该车辆完成,将任务ik+1作为第一个任务,对ik+1ik+2…il重复上述过程,直到所有任务都被分配车辆为止。 2.3.2 目标函数值的确定 本文问题解的目标函数值是下列三部分之和:该解中所使用车辆的启动费用之和,所使用车辆行驶费用之和,所使用车辆到达各个任务的取货点和送货点所产生的违法软时间窗约束的惩罚费用之和。 设c0为单位车辆的启动费用,c1为单位车辆单位里程的行驶费用,那么,若一个解中所有货运任务需要r辆车完成,则该解中总的启动费用为c0*r,设该解中所使用车辆总的行程为d,则该解中所使用车辆行驶费用之和为c1*d。 由于本文的时间窗约束为软时间窗约束,故采取的是加入惩罚的措施,即:对于一个解的每一个集货点或送货点i,若车辆在该点规定时间窗内到达,则不惩罚;若车辆到达该点时间早于该点时间窗的上限或晚于该点时间窗的下限,则加入惩罚,并且早到的惩罚要小于迟到的惩罚。即:若设F表示一个解的违法软时间窗约束的总的惩罚费用,那么: 其中:si表示车辆到达第i个点的时刻,a与b分别表示车辆早到和晚到的单位时间惩罚费用。 (1)选择复制 参考刘国华、包宏、李文超[22]有关文献中的选择复制方法,在种群中,首先计算各个染色体的适应值,将适应值最大和最小的两条染色体挑选出来,让适应值最大者保留下来进入下一代种群,之后将它们从种群中删除,然后对种群采用轮盘赌的方法选择能够进行交叉变异的染色体。 (2)交叉操作 首先将要进入交叉操作的种群中的染色体随机两两配对,得到(n-22对染色体,对这(n-22对染色体中的每一对都产生0-1间的随机数,如果该随机数小于或等于交叉概率pc,那么这对染色体将进行交叉操作。 在要进行交叉操作的两条染色体中,分别任意选取两项货运任务的基因段,进行交叉,从而产生两条新的染色体。如果新生成的子体中存在任务缺失,则将缺失的任务加入新生成的子体之后,如果新生成的子体中存在任务重复,则将重复的任务删除。为说明交叉操作,示例如下: 将第一条父体的基因段任务2与第二条父体的基因段任务3,以及将第一条父体的基因段任务5与第二条父体的基因段任务2进行交叉操作,得到下一代的两条子体: (3)变异操作 step1 生成n-2行l列的0-1随机数矩阵,该矩阵各个位置的元素分别对应变异种群中各个染色体相应位置的任务; step2 对变异种群中每个染色体都进行下列操作:考察该染色体中的各个任务是否满足变异条件,即看该任务对应的随机矩阵中的元素是否小于等于变异概率pm,如果是,则接着考察该任务是否有多个送货点,如果是,则任意选取2个送货点,将其位置进行交换即可。 step1 输入各个车场、各个任务的集货点及送货点的坐标、时间窗;各个任务货运量;单位车辆的启动费用,单位车辆单位里程的行驶费用;交叉概率及变异概率;种群规模;迭代次数;并将次优值设为无穷大,次优解为空。 step2 产生初始种群,种群中包括n条染色体。 step3 计算种群中各个染色体的适应值,将其中适应值最大的和最小的都挑选出来,更新次优解和次优值,将适应值最大者保留进入下一代种群,之后将这两个染色体从种群中删除,转步骤4。 step4 对步骤3最后得到的种群进行遗传操作:即进行选择复制,交叉和变异操作。 step5 将步骤3中适应值最大的染色体复制两次到经过步骤4后得到的种群中,得到新的种群。 step6 判断是否达到迭代次数,若达到迭代次数,则算法终止;否则,对步骤5的新种群转step3。 现有三个车场将其编号为1、2、3,它们的坐标依次为(40,60),(55,30),(80,51),车辆从这三个车场出发共需要完成6项货运任务,任务信息见表1。各个车场的车型都相同,已知每辆车的载重量为q=10,速度v=45,最大行驶距离为180,启动费用及单位里程行驶费用分别设为c0=10,c1=1,另时间窗惩罚系数:早到单位时间的惩罚费用a=4,迟到单位时间的惩罚费用b=7,试安排车辆行驶路线,使总费用最小。 表1 任务信息 用4,5,6,7,8,9依次表示任务1~6的集货点;用自然数10表示任务1的送货点,自然数11表示任务2的送货点,自然数12,13分别表示任务3的第1,2个送货点(20,65)(30,45),自然数14表示任务4的送货点,自然数15表示任务5的送货点,自然数16,17,18分别表示任务6的第1,2,3个送货点(75,29)(66.15)(85,18)。根据本文所提供算法,取交叉概率pc=0.6,变异概率pm=0.1,经过400次迭代后,得到问题的次优解:1→6→12→13→5→11→9→17→18→16→7→14→3→4→10→8→15其次优值为:z=286.77,该次优解含两条路径如表2所示: 表2 次优解的路径信息 本文对多车场开放式带有里程约束的软时间窗集送货一体化车辆路径问题采用遗传算法进行求解,算例表明该算法易于实现,且效果较好。本文为单车型问题,而对于多车型问题我们将进行下一步研究。 [1]Dantzig G.B,Ramser J.H.The truck dispatching problem[J].Management Science,1959,6(1):80-91. [2]Bodin L.,Golden B.,et al.Routing and scheduling of vehicle and grews-the state of the art[J].Computers and Operations Research,1983(10):63-251. [3]Desroslers J.,Laporte G.et al.Vehicle routing with full loads[J].Computers and Operations Research,1988,15:219-226. [4]Savelsbergh M.W.P.,Sol M.The general pickup and delivery problem[J].Transportation Science,1995,29:17-25. [5]Sophie N.P.,Karl F.D.,Richard F.H.A survey on pickup and delivery problems Part I Transportation between customers and depot[J].Fur Betriebswirtschaft,2008,58(1):21-51. [6]Sophie N.P.,Karl F.D.,Richard F.H.A survey on pickup and delivery problems Part II:Transportation between pickup and delivery locations[J].Fur Betriebswirtschaft,2008,58:81-117. [7]Li H.B.,Lim A.A meta-heuristic for the pickup and delivery problem with time windows[C]//Tools with Artificial Intelligence,Proceedings of the 13th International Conference,2001:160-167. [8]Gutiérrez J.G.,Desaulniers G.,et al.A branch and price algorithm for the vehicle routing problem with deliveries,selective pickups and time windows[J].European Journal of Operational Research,2010,206(2):341-349. [9]Gambardella L.M.,Dorigo M.An ant colony system hybridized with a new local search for the sequential ordering problem[J].INFORMS Journal on Computing,2000,12(3):237-255. [10]Lu Q.,Dessouky M.M.A new insertion-based construction heuristic for solving the pickup and delivery problem with time windows[J].European Journal of Operational Research,2006,175(2):672-687. [11]Dumitrescu I.,Ropke S.,et al.The traveling salesman problem with pickup and delivery:polyhedral results and a branch and cut algorithm[J].Mathematical Programming,2010,121(2):269-305. [12]Renaud J.,Boctor F.F.,Ouenniche J.A heuristic for the pickup and delivery traveling salesman problem[J].Computers and Operations Research,2000,27:905-916. [13]Renaud J.,Boctor F.F.,Laporte G.Perturbation heuristics for the pickup and delivery traveling salesman problem[J].Computers and Operations Research,2002,29:1129-1141. [14]李军,郭辉煌.物流配送车辆调度理论与方法[M].北京:中国物资出版社,2001. [15]霍佳震,王新华.基于约束规划求解车辆调度问题[J].物流技术,2005,9:110-112. [16]王兆庚,李建更,程世东.基于遗传算法的集送一体化的车辆路径问题[J].计算机工程应用,2006,42(1):208-211. [17]屈援,汪波,钟石泉.单车场集送一体化车辆路径问题及其混合算法研究[J].武汉理工大学学报,2007,31(5):811-814. [18]钟石泉,贺国光.有里程和时间窗约束的一体化车辆调度智能优化[J].系统工程与电子技术,2006,28(2):240-243. [19]霍佳震,张磊.有时间窗的集货送货一体化车辆路径规划启发式算法研究[J].物流技术,2004,5:64-66. [20]李臻,雷定猷.多车场车辆优化调度模型及算法[J].交通运输工程学报,2004,4(1):83-86. [21]钟石泉,王雪莲.多车场集送一体化车辆调度问题及其遗传算法研究[J].西安电子科技大学学报,2009,19(1):63-68. [22]刘国华,包宏,李文超.用MATLAB实现遗传算法程序[J].计算机应用研究,2001,18(8):80-82.2 遗传算法设计
2.1 染色体结构
2.2 初始种群的产生
2.3 适应值函数的确定
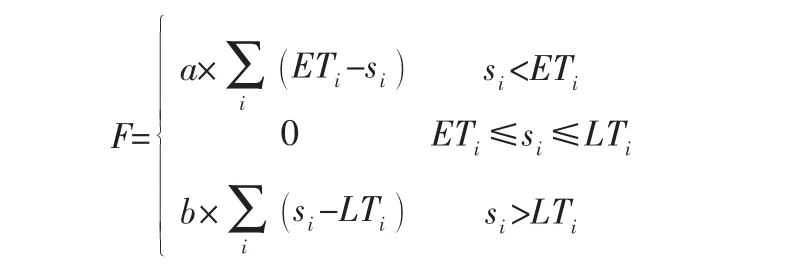
2.4 遗传操作


2.5 遗传算法步骤
3 例 子


4 结 论
