不同发电机模型大扰动特性及暂态稳定性的对比研究
2012-09-03许国瑞康锦萍李和明
贾 瑞,许国瑞,康锦萍,李和明
(华北电力大学电气与电子工程学院,北京 102206)
电力系统的瞬态分析要求有准确的发电机数学模型,选取不同的数学模型,计算结果也会有所不同。在多机系统中,发电机模型的选取在仿真计算上具有可行性。发电机的双反映理论提供了基于发电机等效电路的发电机实用模型,并在电力系统仿真计算中得到广泛的应用。
BPA暂态稳定程序通过时域仿真法分析电力系统的暂态稳定性,发电机模型包含基于2种假设的不同阶数的实用模型,但对于阻尼绕组中涡流集肤效应导致的阻尼参数变化对运行行为的影响,无法在实用模型中进行准确计算。
BPA暂态稳定程序通过发电机的空载饱和特性考察对转子铁心饱和的影响。但在负载运行条件下,铁心的饱和程度与空载特性所表现的不同,即使在额定电压下,不同运行条件下的饱和程度与额定工况下的饱和程度也不同。
山霞等采用电力系统稳定分析BPA软件对典型的4机11节点系统进行了时域仿真计算,针对不同故障切除时间下发电机的转子摇摆曲线,判别电力系统的稳定状态,并对BPA和PSS/E仿真软件的暂稳态数学模型进行分析比较。
时步有限元方法(T-S FEM)计算时考虑到了磁路饱和、磁场畸变、转子铁心与阻尼绕组中的涡流和集肤效应等复杂非线性因素的影响,从而得到系统扰动条件下发电机动态过程的标准响应。对于磁场饱和因素的考虑,T-S FEM对每一时刻下的磁场方程进行准确的非线性迭代计算,并根据各单元磁密的计算结果经B-H特性曲线得到磁导率。以某300 MW汽轮发电机为例,利用有限元方法对同步发电机在不同运行条件下的饱和特性进行了大量研究,分析了同步发电机内部多因素饱和效应对其运行特性的影响,并采用二维平面场进行计算,通过麦克斯韦方程组得到电磁场方程的边值形式,进行了场路网耦合的大扰动算例仿真,考虑转子铁心饱和、阻尼等因素对发电机暂态稳定性的影响。
1 BPA与时步有限元模型
1.1 BPA暂态稳定程序中的模型
BPA暂态稳定程序中的MF卡对应假设A(计及互漏)。在基本假设条件下,若考虑转子D轴1套阻尼绕组、Q轴2套阻尼绕组的作用,通过推导,可得系统分析6阶实用模型,具体包括4阶转子电压方程(1)和2阶转子运动方程(2):
转子电压方程:

转子运动方程:
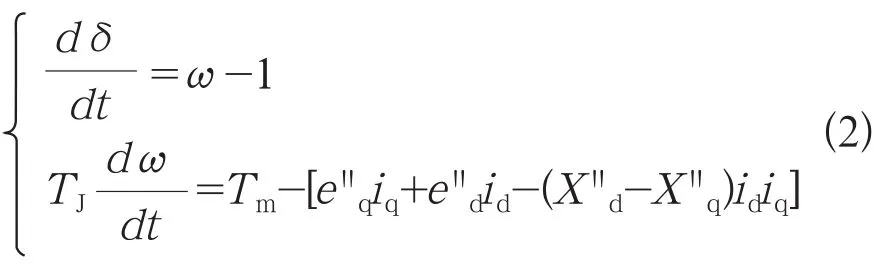
BPA暂态稳定程序中的MG卡对应假设B(不计互漏)。发电机的6阶实用模型包含4阶转子电压方程(3),转子运动方程与MF卡相同。
转子电压方程:

在基本假设条件下,若不考虑Q轴的阻尼绕组,仅考虑D轴的励磁绕组作用, 则MF卡与MG卡对应发电机的3阶实用模型,如表达式(4)所示。

不计阻尼时,MF卡与MG卡中的Tq0'为零,即为仅考虑励磁绕组的发电机3阶模型;计及阻尼时,需要增填M卡中的发电机次暂态参数。
通过这2段折线模拟饱和时的空载特性曲线,MF卡双轴模型得到修正Xd,Xq所需的饱和系数;MG卡双轴模型得到修正实用模型中的暂态电势eq'所需的系数。
1.2 基于时步有限元的场路网耦合模型
仿真模型如图1所示(只给出A相部分)。因Y-d11联结组别的变压器带来相、线之间变换时的相角差,为BPA中数据转换方便,该仿真模型中发电机经Y-y0联结组别的变压器接于无限大电网。若用rf、lf、rs;ls、rt、lt;rL1、lL1;rL2、lL2分别表示励磁绕组电阻与端部漏电感、定子绕组电阻与端部漏电感、变压器电阻与漏电感(折合至低压侧)以及各传输线的电阻与电感。此时发电机定子回路的方程和电网方程分别见公式(5)和公式(6)。
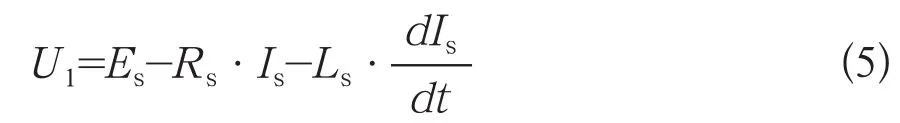
式中:Ul=[uAB,uBC,uCA]T;Es=[eA,eB,eC]T;Is=[iA,iB,iC]T;Rs=diag[rs,rs,rs];Ls=diag[ls,ls,ls]是向量形式,uAB、uBC、uCA是发电机出口处线电压。
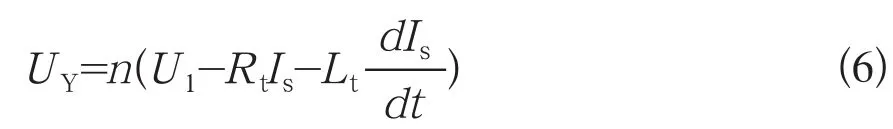
式中:n为变压器变比,UY=[uYA,uYB,uYC]T;Rt=diag[rt,rt,rt];Lt=diag[lt,lt,lt];IY=[iYA,iYB,iYC]。
针对单机无穷大系统的场-路-网耦合形式的时步有限元方程(7)。
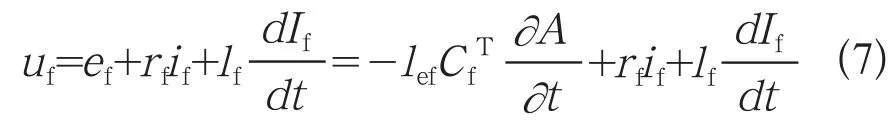
式中:lf为励磁绕组端部漏感,Cf为励磁电流关联矩阵。
忽略定子铁心中的涡流,发电机直线部分采用2维平面场进行计算,通过麦克斯韦方程组得到电磁场方程的边值形式(8)。

式中:μ为磁导率,A为磁位,J为电流密度(包括定子绕组、励磁绕组以及转子阻尼导条的电流密度)。
针对单机无穷大系场的场一路一网耦合形式的时步有限元方程(9)。

图1 单机无穷大系统模型
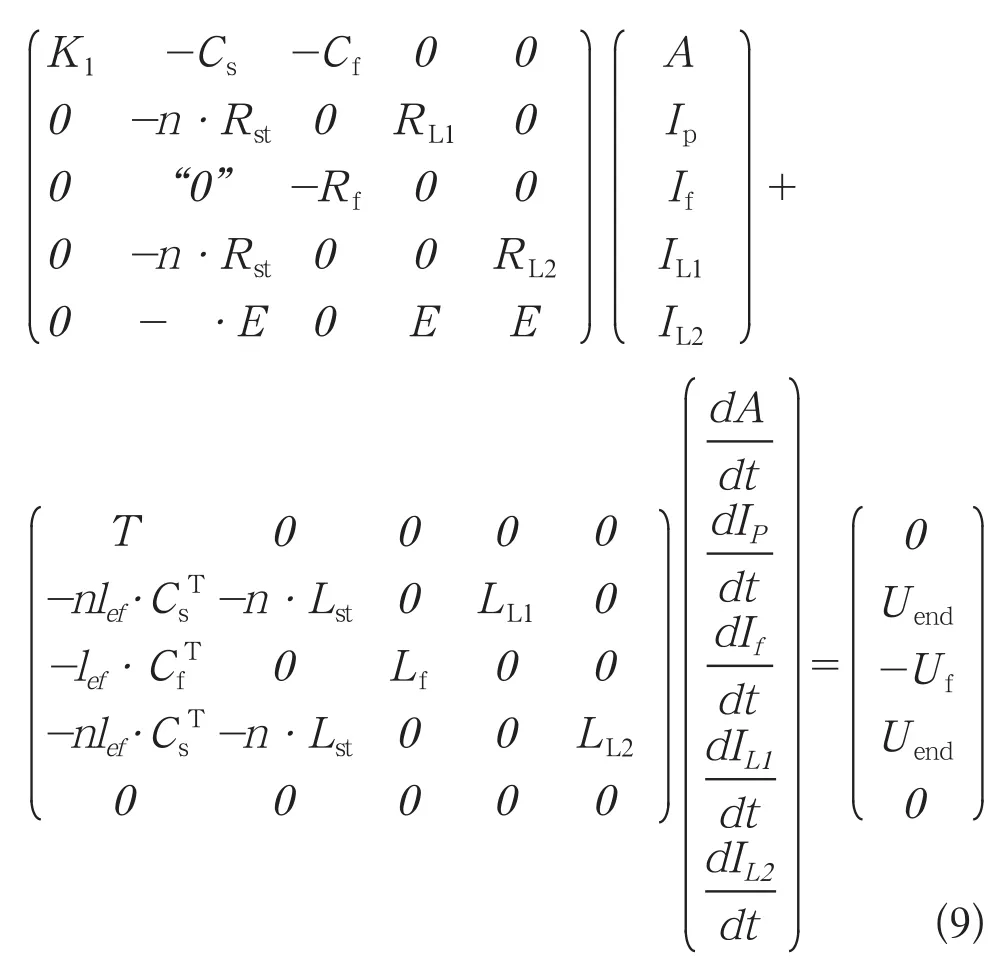
式中:Rst=Rs+Rt;Lst=Ls+Lt;E=diag[1,1,1];Uend表示无限大电网的电压。
2 发电机模型大扰动特性的比较
BPA所需的单机无穷大系统地理接线如图2所示。Gen1、Bus0选为PQ节点,Gen2选为平衡节点,各节点电压等级和传输线阻抗标记于图2中。BPA与T-S FEM的潮流计算结果如表1~4所示。
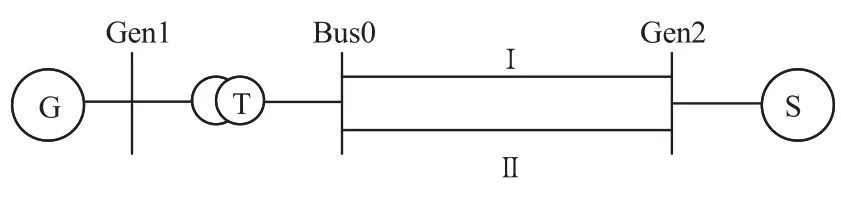
图2 潮流程序地理接线

表1 不计饱和、不计阻尼情况
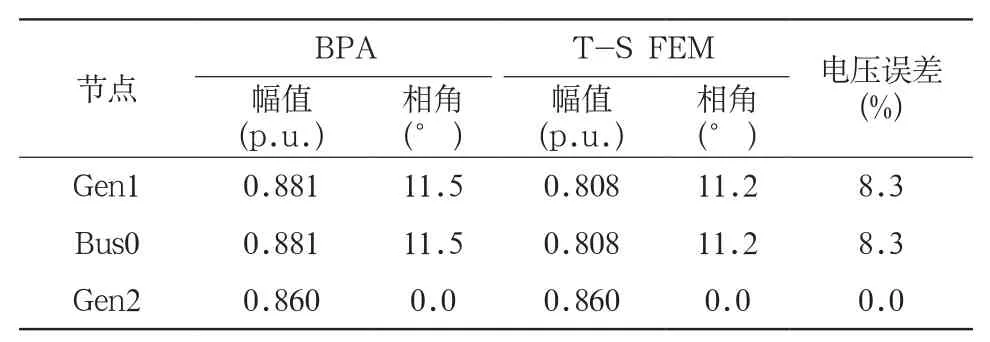
表2 计饱和、不计阻尼情况
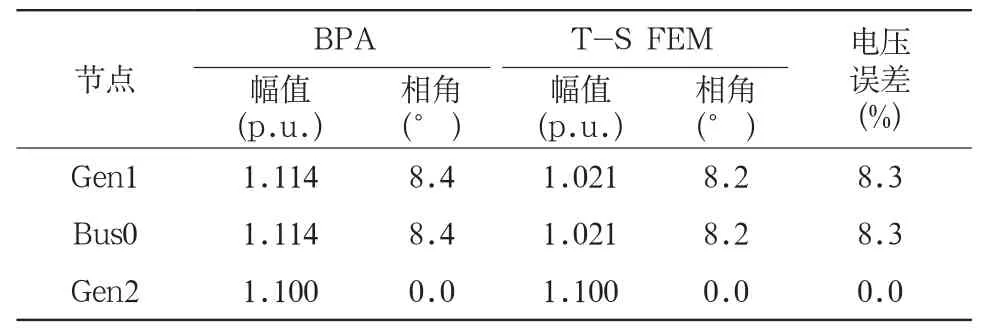
表3 不计饱和、计阻尼情况

表4 计饱和、计阻尼情况
图3为BPA暂态稳定程序考虑饱和时采用300 MW发电机实测空载饱和特性曲线。

图3 发电机的空载饱和特性
在图3中,虚线表示发电机的空载饱和特性,经最小二乘拟合后可表示为公式(10)。
从横坐标上可查得空载电压为1.0倍额定电压和1.2倍额定电压时的励磁电流值,从而得到修正Xd、Xq所需的饱和系数。将潮流结果BSE文件代入BPA暂态稳定程序,无穷大电网可用MC卡填写,其中EMWS为 999 999。
对于单机-变压器-双回线-无穷大系统发生的大扰动情况,在不同条件下,采用不同模型对发电机暂态过程进行仿真计算。仿真条件为:正常运行0.2 s后发生传输线I三相短路(其中短路位置在基1/2处),短路持续0.1 s后保护动作切除故障线路,再经0.4 s后故障排除,重合闸成功。
2.1 不计饱和、不计阻尼情况
在此情况下,发电机的实用模型对应为3阶,T-S FEM模型对应于全部求解区域采用线性计算,涡流区域电导率均为0。发电机的大扰动动态响应结果如图4所示。
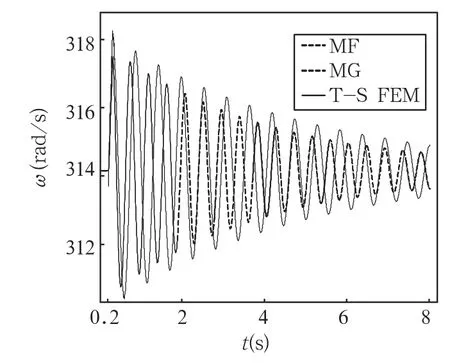
图4 不计饱和、不计阻尼时发电机的转速曲线
2.2 计及饱和、不计阻尼情况
考虑磁场饱和且不计阻尼绕组作用时,发电机的实用模型仍为3阶模型,但其电抗参数则不再为常数,应随着运行工况进行相应的调整。
T-S FEM对应于铁磁材料区域采用非线性计算,涡流区域的电导率为0,发电机的大扰动动态响应结果如图5所示。
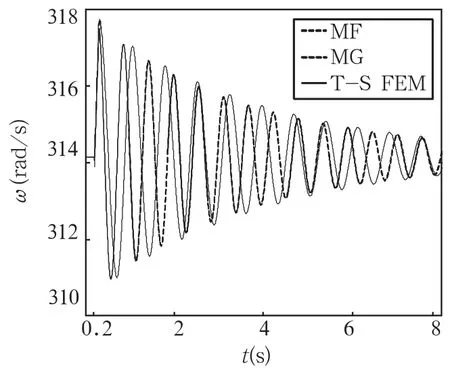
图5 计饱和、不计阻尼时发电机的转速曲线
通过上述两图可知:计及饱和后,BPA与T-S FEM的计算结果较为接近。这是因为Gen1节点的PQ由T-S FEM获得,实际上已经在潮流计算中计及饱和对发电机输出功率的影响。MF卡与MG卡的转速曲线重合,这是因为不考虑阻尼作用时忽略了阻尼互漏电抗的影响。BPA与T-S FEM都对应发电机的3阶模型。
2.3 不计饱和、计及阻尼情况
不考虑磁场饱和而计及阻尼绕组作用时,发电机的实用模型对应为6阶模型,T-S FEM模型对应于全部区域线性计算,涡流区域电导率不为0。发电机的大扰动动态响应结果如图6所示。
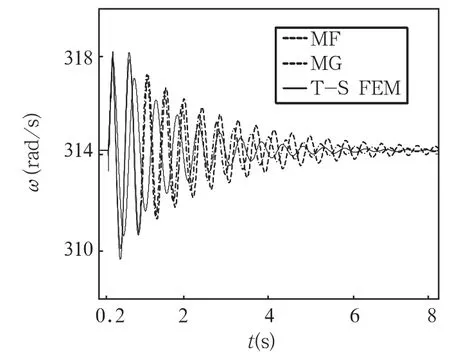
图6 不计饱和、计阻尼时发电机的转速曲线
2.4 计饱和、计阻尼情况
计及磁场饱和与阻尼绕组作用时,发电机的实用模型对应为6阶,T-S FEM模型在铁磁材料区域采用非线性计算,涡流区域电导率由实际材料属性决定。发电机的大扰动动态响应结果如图7所示。
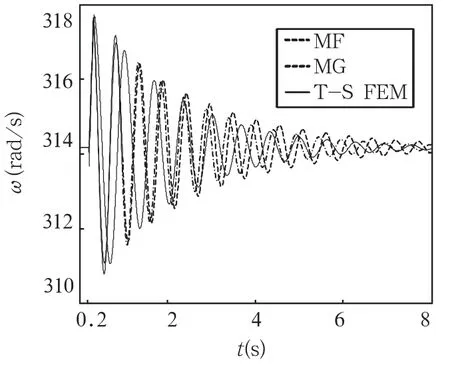
图7 计饱和、计阻尼时发电机的转速曲线
从图6和图7可以看出:计及阻尼影响后,MF卡(计及互漏)的计算结果较MG卡(不计互漏)更接近T-S FEM。
采用prony方法对大扰动过程的发电机中转速振荡频率和衰减特性进行分析,结果如表5~表8所示,同时还在表中列出了MF卡和MG卡与T-S FEM计算结果的误差。在表中:n表示振荡频率,λ表示衰减系数。
由表5~表8可得出以下结论。
(1) 与FS FEM相比,BPA转速曲线的振荡频率较大,这主要是由于BPA中发电机的实用模型忽略了定子绕组的暂态过程。当功角较大时,主磁通的磁力线不是沿径向穿过气隙,而是沿倾斜方向穿过气隙进入定子槽,从而导致等效气隙变大。

表5 不计饱和、不计阻尼情况
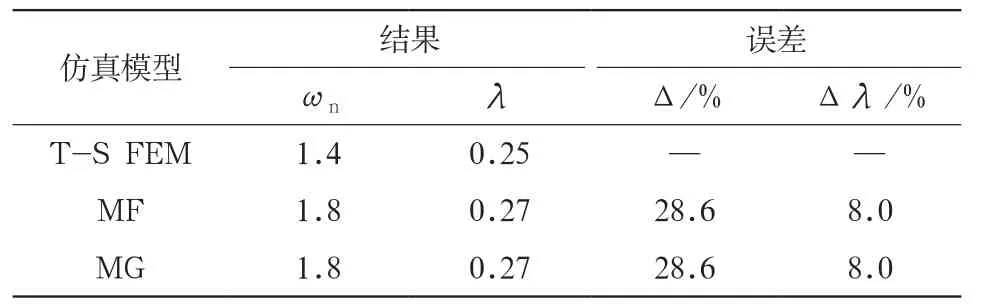
表6 计饱和、不计阻尼情况

表7 不计饱和、计阻尼情况
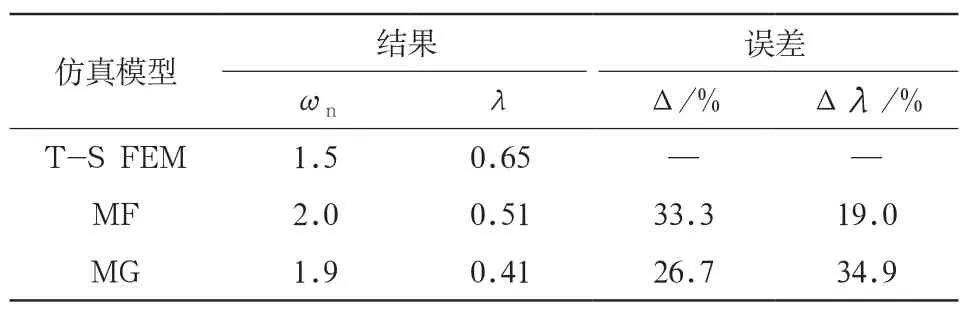
表8 计饱和、计阻尼情况
(2) 计及饱和时,尽管BPA采用T-S FEM计算得到了稳态初值和空载饱和特性曲线,但其计算结果与T-S FEM仍存在差异,尤其是计及阻尼作用时,误差明显变大。这表明BPA难以准确考虑转子铁心饱和、阻尼绕组作用等复杂非线性因素对发电机暂态稳定性的综合影响。
(3) 计及阻尼绕组作用后,发电机转速曲线的衰减系数明显变大。系统发生扰动后,阻尼绕组能使发电机尽快恢复至稳定状态,不会导致失步。
3 临界故障清除时间的比较
电力系统暂态稳定指的是电力系统受到大干扰后,各发电机保持同步运行并过渡到新的或恢复到原稳定运行状态的能力。电力系统的暂态稳定性对系统而言至关重要,因为当系统遭受短路故障、断线故障、大容量机组解列等较大振动时,若系统不能保持暂态稳定,将导致机组失步、系统解列甚至崩溃。临界故障清除时间是评估系统暂态稳定极限的重要指标。
BPA用时域仿真的方法对系统最为关注的临界故障清除时间tout进行计算,并结合二分法反复迭代,得到切除故障线路所需时间tcct。即系统正常运行0.2 s后发生传输线三相对地短路,经tcct后切除线路,发电机功角经过振荡趋于收敛,系统恢复稳定;经tout秒后切除线路,发电机功角趋于发散,系统失稳。发电机采用不计及转子铁心饱和、计及阻尼的6阶实用模型,其计算结果如图8所示。

图8 功角曲线
经T-S FEM计算临界故障清除时间tcct为0.262 s。忽略转速影响和定子磁链影响,BPA发电机实用模型得到的tcct偏小,稳定性评估偏保守。
4 结束语
针对2种思想建立单机-变压器-双回线-无穷大电网系统在受到大扰动时的动态过程,分别讨论了转子铁心饱和及阻尼绕组对瞬态响应带来的影响,并就系统的临界故障清除时间进行了计算。
计及饱和时,为了保证仿真条件上的一致性,BPA使用由T-S FEM计算得到的稳态初值。当忽略阻尼绕组的作用时,BPA的计算误差小于考虑阻尼绕组时的计算误差。可见,BPA用空载饱和特性来代替整条曲线不能精确反映发电机饱和时的状态。T-S FEM针对每一时刻的磁场方程进行了准确的非线性迭代计算,根据各单元磁密的计算结果和B-H特性曲线得到其磁导率的方法更为精确。阻尼绕组对瞬态响应的影响比较明显,系统大扰动过程中,阻尼绕组漏电抗的作用不可忽略,利用BPA计算暂态稳定性时,建议采用MF卡。
BPA实用模型忽略了转速和定子磁链的影响,在暂态稳定性的计算中较为保守;此外,与MF卡相比,MG卡(忽略转子漏电抗的影响)的计算结果较小。可见,BPA只能给出故障临界清除时间的粗略范围,仅可作为暂态评估的参考。
1 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
2 王泽忠,全玉生,卢斌先.工程电磁场[M].北京:清华大学出版社,2005.
3 周 济.同步发电机不同运行条件下多因素饱和效应的研究[D].北京:华北电力大学,2000.
4 山 霞.基于BPA的电力系统暂态稳定时域仿真研究[J].电工文摘,2010(3).
5 罗应立,胡 笳,刘晓芳,等.面向系统动态分析的场路网耦合时步有限元模型[J].中国电机工程学报,2009(33).
6 中国电力科学研究院编.PSASP电力系统综合分析程序暂态稳定手册[M].北京:中国电力科学研究院,2003.
7 刘 剑.Prony在电力系统低频振荡控制中的应用[D].成都:四川大学,2006.
