基于改进势场法和B样条曲线的无人直升机电力巡线航路规划

李文进，高洪雨，韩晓萍

（1.国网技术学院，山东 泰安 271000；2.山东大学 电气工程学院，山东 济南 250061）

我国电力无人直升机巡线时，利用装载检测设备的直升机对高压输电线路上的发热故障隐患和外部缺陷进行检测，以提高巡线的工作效率.由于巡线任务多在植被茂盛的山林地区进行，树闪故障成为限制无人直升机巡线广泛应用的最大限制因素.为了实现巡线过程中的有效避障，直升机的航路规划显得尤为重要.当选择规避策略时，三维空间规划可简化为水平航路规划.根据具体使用环境和要求不同，已提出梯度法、遗传算法（GA）、模拟退火算法（SA）、蚁群算法（AS）、人工势场法［1］等多种方法，其中人工势场法是一种虚拟力法，具有反应速度快、计算量小和实时性等优点［2］，其快捷的环境描述形式在实时避障和平滑轨迹控制等方面得到广泛应用.

人工势场法由Khatib于1986年提出，它是对运动环境的一种抽象描述，其基本思想是构造由目标点引力和障碍物的斥力共同作用的人工势场，搜索势函数梯度下降的方向来寻找无碰撞路径［3］.考虑到传统的人工势场没有对规划路线的评价指标以及容易出现局部极小等自身缺陷［4］，本文对其进一步优化，并采用圆域B样条曲线和改进人工势场相结合的航路规划方法.根据构造的势场函数特点，沿等势线方向进行路径搜索，在避免局部极小值问题的同时，引导直升机快速绕过障碍物后继续向目标点飞行.实验结果表明，本文提出的方法能满足复杂环境下的实时性要求并达到良好的航路规划效果.

1 改进的势场函数

1.1 斥力势场函数

假设平面内有n个障碍物，障碍物为任意多边形，第j个障碍物可用区域Sj来表示:

其中该障碍物的边界满足:fj（x）＝0，则定义函数pj（x）为

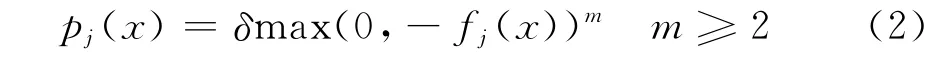
δ是一个极大的正值，称为罚值系数.则对该障碍物的外部区域fj（x）＝0，并且在区域Sj的内部pj（x）存在极大值.因此这样的函数pj（x）满足用于航路规划的势场函数的基本需求，可以很好的作为势场函数的模型.

若把无人直升机看做一个质点，则当它通过含有N个障碍物的空间区域时，这N个障碍物可被表示为

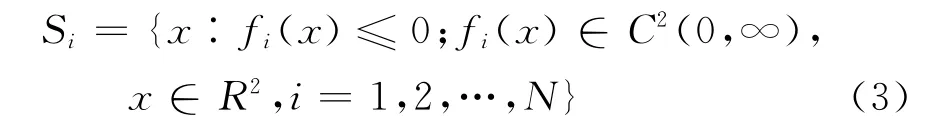
则定义任意一点的斥力势场函数P（x）为

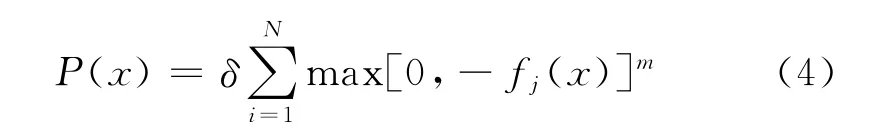
P（x）为公式（2）定义的单个障碍物斥力势场函数Pj（x）的累加，文献［5］已经证明，在非障碍物的区域内P（x）不会出现局部极大值点（设为Pmax），Pmax仅可能出现在障碍物S区域内.

1.2 引力场函数

本文采用圆锥曲线函数

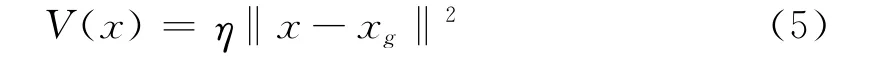
作为引力势场函数.其中η为小的常数.xg为目标点所在的位置，该引力势场函数在点xg具有全局最小值.

1.3 空间区域势场函数

斥力势场函数和引力势场函数的和提供了无人直升机飞行的空间区域势场函数，定义为U（x），则

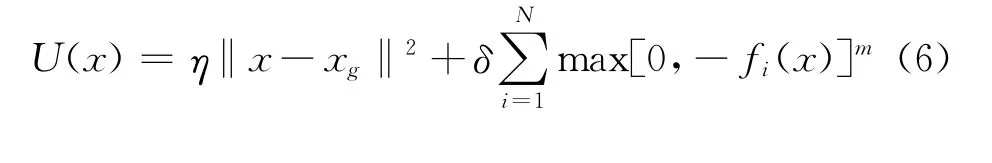
公式（6）定义的势场函数U（x）在无人直升机飞行的空间区域内仅在目标点xg处出现唯一的全局最小值，证明如下.

在空间区域中势场函数U（x）的最速下降方向（负梯度方向）为

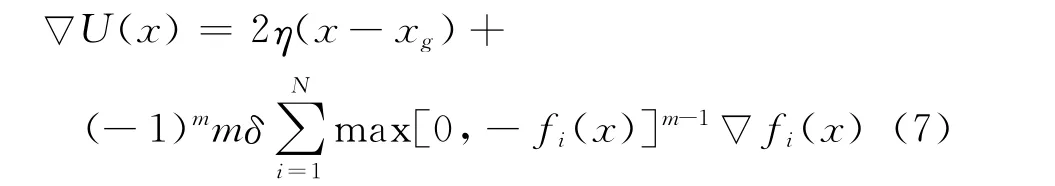
由于罚值系数δ的存在，各个障碍物的内部是无人直升机无法到达的区域.若排除了各个障碍物内部的所有点，在其他的区域中，公式（7）的第二项始终为零.当且仅当x＝xg时，▽U（x）＝0，即势场函数U（x）仅在目标点xg处存在全局最小值点.

在实际避障实验中，由于本文把无人直升机看做一个质点，且由公式（2）得知，直升机有可能沿着障碍物的边界飞行而出现误碰现象导致避障失败.为了解决此问题，考虑直升机距离障碍物的安全距离Dmin，引入安全系数eλ，λ＞0，相当于把每个障碍物的边界虚拟扩大化，从而有效地避免出现误碰现象的发生.则最终的空间区域势场函数U（x）为

图1，图2分别为空间区域存在两个圆形障碍物时，按照公式（8）绘制的势场及其等高线图.可以看出任意一条势场等高线都是以目标点G为圆心，半径为r的圆.下面将介绍按照势场的下降方向进行航线路径搜索的方法.

图1 存在两个圆形障碍物时的势场

2 航线路径搜索

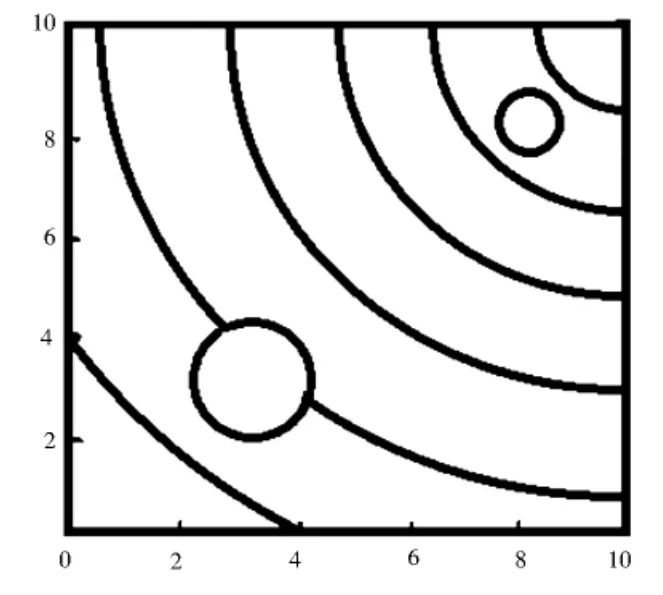
图2 为两圆形障碍物存在的势场等高线图

当无人直升机飞行的空间区域不存在障碍物时，连接起始点S和目标点G的线段即是最优飞行路径［6］.路径搜索方法是以理想线段LSG为直径所代表的圆形区域为最大可行搜索域.图2为存在两个障碍物时的路径搜索.在搜索过程中，首先均分起始点S和目标点G间的线段LSG，并以起始点S和任意均分点之间的线段作为圆形区域的直径，以该圆形区域为可行搜索域，搜索该区域内的势能最小值，记录该值所在的位置.如果临近搜索域所确定的临近势能最小值的位置发生较大变化，则记录将要发生变化的点，并用该点代替最初的起始点S，开始新的循环，具体操作如下:

（1）如图3所示，将连接起始点S和目标点G的直线段LSG均分为M段，则LSG上共有M＋1个点（包含S和G点），设Ai为LSG上任意一点，Circle（AiG）是以Ai和G间的线段为直径的圆形区域，则区域Circle（AiG）为全局搜索域.定义区域Circle（SAi）为第i次的搜索域.

（2）无障碍物存在时，在区域Circle（SAi）内的势能最小点必为点Ai.即无障碍物存在时，任一搜索域内的势能最小值点必然在该直线段LSG上.

（3）若存在障碍物，则障碍物附近局域势能最小值点必然落在障碍物边缘的空间区域上.

（4）若障碍物的顶点落在搜索区域内时，临近搜索域的局部势能最小值的位置坐标发生的变化超过规定的阈值ε时，记录前一个最小值的位置坐标，设为As，以As为子起始点，且目标点G不变，更新全局搜索域为Circle（AsG），重复进行该过程，找到所有的子起始点，直到局部最小值点为G点停止.如图所示，所有的子起始点分别记为点1，2，3，4，5.

（5）连接S、一系列的子起始点（1，2，3，4，5）、G，得到的路径就是所求搜索路径.

3 圆域B样条曲线及路径修正

3.1 圆域B样条曲线

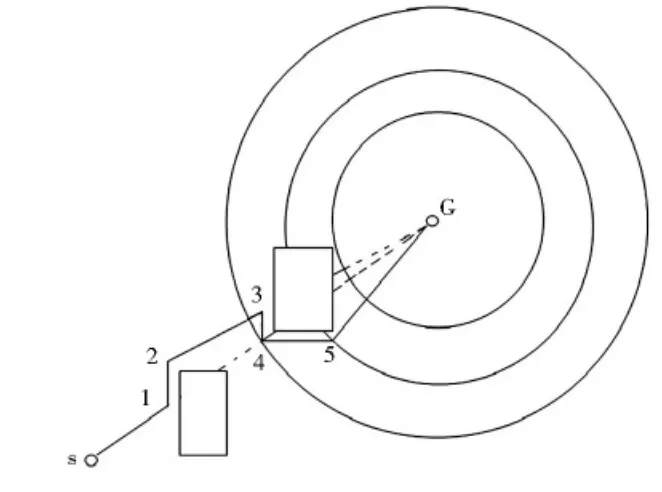
图3 航线路径搜索方法

在图3所示的航线路径中，有的航线段间隔特别小（如航点3、4之间的航线段），这不利于直升机及时产生操作指令控制飞行姿态.要求航路各点的间距满足一定的距离限制，使直升机在每一段航路飞行时都有足够的时间去响应控制命令，因此对航路进行进一步的修正和调整.结合B样条曲线具有C2连续性、局部性及B样条曲线的曲率变化较均匀的特点［7－8］，本文采用B样条函数对航路进行曲线拟合.在拟合曲线上按照满足航路点间距要求来修正并给定最终的航路点.

定义1对于正整数k，m（m≥k－1），T＝ ｛t0，t1，…，tm＋k｝为一个非递减的参数序列，Ni，k，T（t）为定义在该参数序列T上的B样条基函数，则称点集

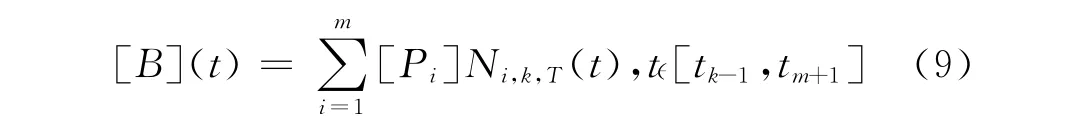
为定义在参数序列T上的k阶k－1次圆域B样条曲线，其中

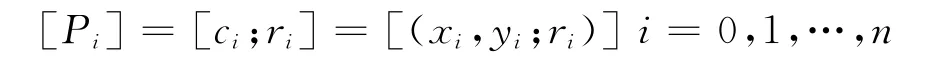
为圆域控制顶点.由圆域算术公式知［9］，式（9）可表示为

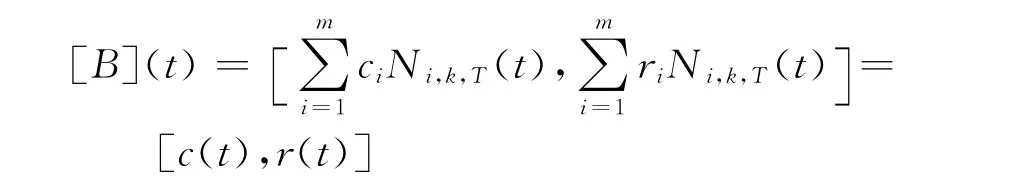
其中c（t）＝ （x（t），y（t））和r（t）分别为中心B样条曲线和半径B样条函数.本文应用三次圆域B样条曲线对搜索航路进行平滑和修正.图4所示是一条四阶三次圆域B样条曲线.

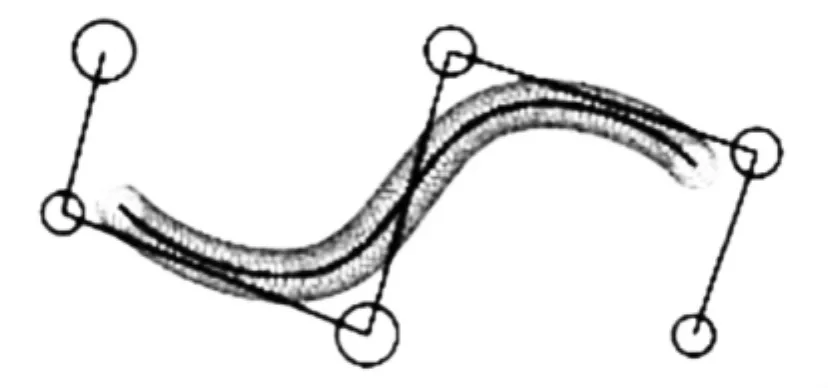
图4 四阶三次圆域B样条曲线

3.2 搜索路径修正

以图3为例，利用圆域B样条曲线对该搜索航路进行修正，点1，2，3，4，5为该样条曲线的控制顶点，则需要对点S，1，2，3，4，5，G所组成的折线LSG进行修正（修正后的路径如图5、图6所示）.

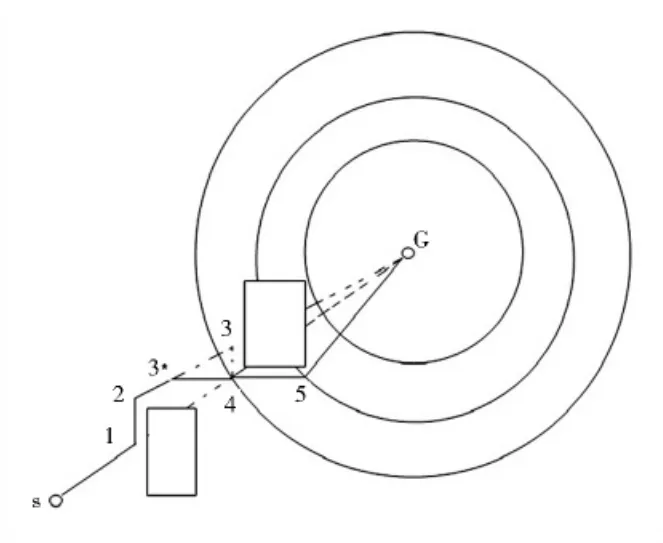
图5 航路修正后的最终飞行路径

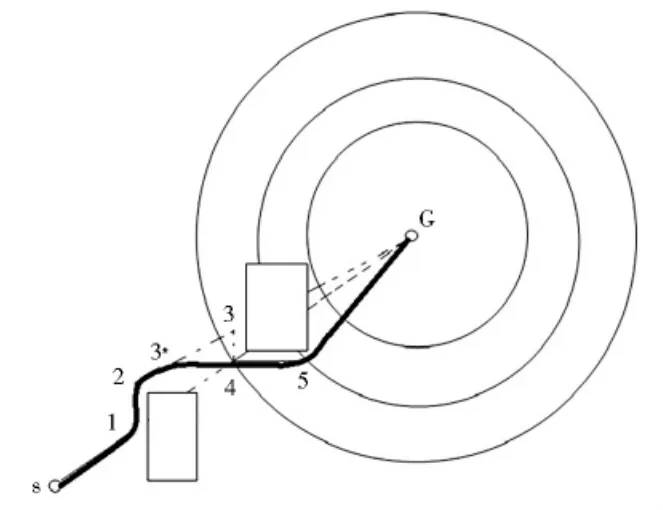
图6 利用圆域B样条曲线进行轨迹平滑路径图

（1）设Di，i＋1为相邻两控制顶点i，i＋1间的航线段距离，D0为直升机能响应控制命令的最短距离.D0可由直升机的一般飞行速度v0和响应时间T0求出，D0＝v0T0，若Di，i＋1＞D0，则该航线路径无变化，若Di，i＋1≤D0，则需对该航线段进行调整.

（2）Di，i＋1≤D0时，如航线段D3，4，则沿控制顶点4延长航线段D4，5与航线段D2，3相交于点3＊，记录点3＊的位置并判断D2，3＊＞D0是否成立.若成立则取点3＊为新的航路控制顶点，更新搜索航路为点S，1，2，3＊，5，G所组成的折线段LSG＊.若D2，3＊≤D0，则重复该过程，找到与航线段D1，2的交点2＊，并进行判断.

（3）当所有航线段Di，i＋1修正完毕后，利用圆域B样条曲线对修正后的航路进行轨迹曲线平滑，得到直升机飞行的最终路径.

对于三次B样条曲线，改动控制多边形上一个顶点，只影响以该点为中心的邻近总共4段曲线［10］.在进行搜索航路修正的过程中，在保证其他控制顶点不变的前提下，重新修正后的航路可以与原来的部分光滑连接.因此在提高航路规划可靠性的同时，不必进行全部航路的重新搜索，从而节省了时间.

4 结束语

本文构建了新势场函数，按照势场下降方向来搜索飞行航路，该方法简单，计算速度快，实时性高.实验表明采用圆域B样条曲线修正航路较好地解决了修正部分的航路与原搜索航路的光滑连接问题，可使无人直升机满足飞行条件的要求到达目标点.该航路规划方法为解决无人直升机飞行中的规避障碍物问题提供了较好的解决方案.

［1］张祺，杨宜民.基于改进人工势场法的足球机器人避碰控制［J］.机器人，2002（1）:12－15.

［2］Mitchell J S B，Keirney D M.Planning strategic path through variable terrain data［C］／／Proceedings of the Applications of Artificial Intelligence.USA:SPIE Press，1984:172－179.

［3］Khatib O.Real－time obstacle avoidnce for manipulators and mobile robots［J］.The international Journal of Robotics Research，19865（1）:90－98.

［4］黄炳强，曹广益.基于人工势场法的移动机器人路径规划研究［J］.计算机工程与应用，2006（27）:26－28.

［5］Hwang Y K，Ahuja N.A potential field approach to path planning［J］.IEEE Transactions on Robotics and Automation，1992，8（1）:23－32.

［6］唐强，王建元，朱志强.基于粒子群优化的三维突防航迹规划仿真研究［J］.系统仿真学报，2004，16（9）:2033－2036.

［7］李栋，冯婷.基于B样条的直升机航迹处理方法［J］.航空计算技术，2008，38（1）:32－35.

［8］Boehm W.Inserting new knots into B－spline curve［J］.Computer Aided Design，1980，12（4）:199－201.

［9］Kevin B J，Timothy W M.Spline Based path planning for unmanned air vehicles［C］／／AIAA Guidance，Navigation，and Control Conference and Exhibit.Montreal，Canada:AIAA，2001:4238.

［10］李栋，曹义华，苏媛，等.基于改进蚁群算法的航迹规划［J］.北京航空航天大学学报，2006，32（3）:258－262.