基于幅值限定积分器的永磁同步电机直接转矩控制系统

孟高军

(东南大学，江苏南京 210000)

0 引言

1985年，直接转矩控制理论被德国鲁尔大学的德彭布罗克教授首次提出。直接转矩控制技术在很大程度上解决了矢量控制中电机参数影响较大，旋转变化非常复杂，以及实际中应用和理论结果不一致的现象。直接转矩控制技术诞生以后，由于具有新颖的控制思想，简洁明了的系统结构，优良的动、静态性能而受到了普遍注意，得到了迅速发展。目前，该技术已成功应用在电力机车牵引的大功率交流传动上。德国、日本、美国都开始发展此项技术，预计21世纪中旬会有较大发展［1］。

与矢量控制技术不同的是矢量控制诞生以后，很快应用到了永磁同步电机上，直接转矩控制提出以后，并没在永磁同步电机上得到应用［2-3］。直接转矩控制开始在永磁同步电机上应用是在1998年由胡育文教授和汤立新博士提出永磁同步电机直接转矩控制理论以后。在直接转矩控制系统中，需要计算定子磁链，构成磁链自控制;需要定子磁链实现电机电磁转矩的准确观测;电机低速运行时需要定子磁链构成磁链量的闭环控制，以实现系统低速时定子磁链量的控制。因此，定子磁链的准确获得是实现直接转矩控制系统高性能的转矩动态响应的关键因素之一。为此，学者们开始进行了更为深入的研究和拓展，形成了一系列新型改进磁链观测器。在各种改进模型中，以Jun Hu和Bin Wu二人在1998年提出的一系列改进观测器较为全面［4］，本文主要介绍的是他们提出的幅值限定的积分器，并针对该积分器在系统应用中存在的不足，提出了一种改造方案。

1 基于幅值限定积分器的直接转矩控制

1.1 幅值限定积分器的原理和构造

改进型积分器的结构如图1所示。其输入变量为反电势，输出变量为定子磁链。这种改进积分器的基本思路可以通过式(1)来表示［5］:

图1 幅值限定的积分器

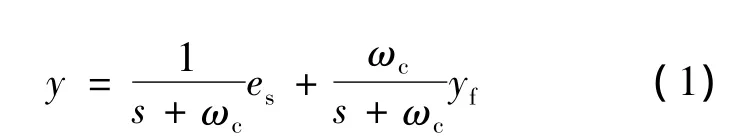
式中:es——积分器输入信号;

yf——反馈信号。

这些观测器采用反馈方式来改善磁链观测精度。假设反馈信号为0的话，此时的积分器为一节惯性滤波器。若当观测器输出y作为反馈信号，那么改进积分器相当于纯积分器。故适当选择反馈信号，改进积分器就会获得较纯积分器和一节惯性滤波器更为优越的性能。

为了减小输出定子磁链的相位失真，该积分器对观测的定子磁链矢量幅值进行饱和限幅，而观测的磁链相位不失真地反馈到输入端，因此对信号相位没有影响。该方案有效解决了磁链波形畸变问题，从而改善了积分器输出信号的质量。但是该方案还存在磁链幅值及饱和基准之间的设定问题，磁链估计的准确性仍然受到饱和限幅基准选取的影响，且该算法要求电机磁链幅值恒定，不适用于电机磁链幅值变化的场合。

1.2 基于不同的直接转矩控制的仿真结果与比较

先对带有纯积分器的永磁同步电机直接转矩控制采用MATLAB/Simulink进行仿真［6］，然后用幅值限定积分器代替原有的纯积分器再次仿真，得出两者的仿真结果，并进行比较。图2～图5就是关于两种不同积分器下的磁链轨迹和转速波形。由图可看出采用幅值限定的积分器的磁链轨迹更加圆滑，转速波形更加平稳。其中电机参数如下:np=4，Rs=2.70，Ld=0.6mH，Lq=3.0mH，ω=40 rad/s。从图2～图5可明显看出，采用幅值限定积分器比用纯积分器有更好的性能。如果不改变其他参数，把电机转速从原来的 40 rad/s增大到100 rad/s，然后再观察磁链轨迹和转速波形，如图6和图7所示。

图5 采用幅值限定积分器的转速波形

从图6、图7可看出，转速没有改变之前相比磁链轨迹已经不再圆滑，而转速也已经不再稳定，出现了很大的波动。通过阅读资料和分析，可以得出出现这种情况的原因，下面对原因进行具体分析。

由前文可知式(1)为幅值限定的改进积分器的基本原理，以α相为例，可以把式(1)写成如下形式:

如果假设ψ'α为tψα，其中t为常数且大于零，那么式(2)可化简为

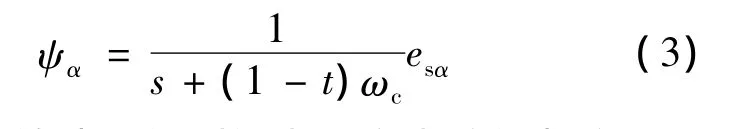
对于不同的转速所得到的电压和电流的频率是不同的，故所得到的电动势es的频率也是不同的，即使截止频率ωc相同，由式(3)可看出，所得到的ψα幅值仍然不同，由于ψα幅值不同，同理可得到ψβ幅值也是不相同的，最后可以推出对于幅值限定的改进积分器所得到的磁链幅值|ψ|也是不相同的，但仍将其与保持不变的磁链给定值进行比较，故将会造成控制性能下降甚至失败的情况。

2 基于幅值限定积分器的改进方案

2.1 改进原理

针对上述情况，可以考虑运用状态方程来求得定子磁链幅值，然后与给定磁链进行比较，这样就可以避免上述不利因素，得到空间电压矢量选择表的一个输入量，如果全部采用状态方程，那么磁链的相位就无法确定，考虑到幅值限定的改进积分器对于相位的确定是非常准确的，所以仍然把幅值限定积分器作为确定磁链相位的工具，再加上状态方程确定磁链幅值，两者一起可以得到很好的效果。

永磁同步电机在d-q坐标系下的电压和磁链的方程为

式中:ω——转子旋转电角速度;

p——微分算子。

由式(4)和式(5)可得

2.2 改进后的仿真模型和仿真结果

图8为改造后的永磁同步电机直接转矩控制系统，为了方便认识和理解，对于这个模型，做出了详细的标注。

图8 改造后的永磁同步电机直接转矩控制系统

针对上述改进积分器下的直接转矩控制模型进行仿真，图10和图11分别为改进之后，在100 rad/s的转速下的磁链轨迹、转速波形的仿真结果。通过改进后的磁链轨迹和转速波形可以很明显地看出，当转速变为100 rad/s时，在幅值限定的改进积分器下，直接转矩控制仍保持了很好的性能。

3 结语

本文主要是对永磁同步电机直接转矩控制系统的仿真模型建立和仿真结果进行分析，首先对纯积分器、幅值限定积分器，这两种不同积分器下的直接转矩控制进行仿真，并且比较他们的磁链轨迹和转速波形。如果不改变其他参数，把转速提高到100 rad/s，幅值限定的积分器的性能和效果会变得很差，故提出了状态方程和积分器共同作用，由状态方程确定磁链幅值，由积分器来确定磁链相位，以取代之前只依靠积分器判断磁链幅值和相位的方法。通过仿真发现经过该方法改进后取得了很好的效果。

［1］陈伯时，陆敏逊.交流调速系统［M］.北京:机械工业出版社，1998.

［2］ZHONG L，RAHMAN M F，HU W Y，et al.Analysis direct torque controller for permanent magnet synchronous motor drives［J］.IEEE Transactions Energy Conversion，1997，14(3):637-640.

［3］田淳，胡育文.永磁同步电机直接转矩控制系统理论及控制方案的研究［J］.电工技术学报，2002，17(1):7-11.

［4］杨永明，孙才新，李新.局部放电在线监测中干扰的识别及抑制方法的研究［J］.仪器仪表学报，1999，20(3):242-243.

［5］HU J，WU B.New integration algorithms for estimating motor flux over a wide speed range［J］.IEEE Trans on PE，1998，13(5):969-977.

［6］李三东，薛花，纪志成，等.基于MATLAB永磁同步电机控制系统的仿真建模［J］.江南大学学报，2004，21(2):44-45.