函数中易混概念剖析

☉江苏省天一中学 何爱君

函数中易混概念剖析

☉江苏省天一中学 何爱君

函数是高中数学的重点内容，贯穿高中数学的始终，各个章节都能见到函数的身影，且数学概念千变万化，给人的感觉不尽相同.解题中由于不能准确地区分概念的内涵和外延，常使解题出现错误，本文以函数中易混淆的几对概念举例说明，供参考.

一、“定义域”与“恒有意义”

二、“值域为D”与“f（x）∈A恒成立”

三、“D内有解”与“解在D内”

例3 关于x的方程x2－2mx+m2－1=0的解在区间（2，5）内，求m的取值范围.

错解：易求得x1=m－1，x2=m+1，由题意有2＜m－1＜5或2＜m+1＜5，即3＜m＜6或1＜m＜4，故1＜m＜6.

错因剖析：“方程f（x）=0在D内有解”中只要求方程f（x）=0在D内至少有一解就可以了，并不要求方程的所有解都在D内；“方程f（x）=0的解在D内”中要求方程的所有解均在D内.本题属于解在区间内的问题.

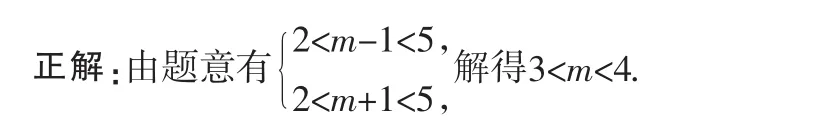
四、“f［g（x）］的反函数”与“f－1［g（x）］”

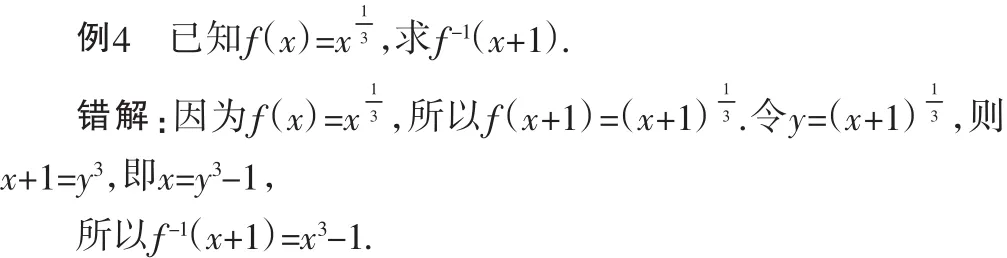
数u=g（x）代入函数f（x）中得到关于x的解析式y=f［g（x）］，再求其反函数，而f－1［g（x）］是先求得函数y=f（x）的反函数y=f－1（x），再将u=g（x）代入即得.

错误在于分不清“f－1（x+1）”与“f（x+1）的反函数”两个概念的差别.f－1（x+1）是f－1（x）在x+1处的函数值，而“错解”求的是f（x+1）的反函数（即y=x3－1）.

综上，因为概念混淆造成的错解问题屡见不鲜，本文抛砖引玉以期提高我们的警戒，请同学们在学习过程中不断归纳总结，以便减少错误的发生.

错因剖析：“f［g（x）］的反函数”与“f－1［g（x）］”两个概念有实质的区别，体现在求法上的不同是：f［g（x）］的反函数是先将函