2012年高考数学的知识总结——排列、组合和概率

☉江苏省泗洪中学 孙艳艳

2012年高考数学的知识总结
——排列、组合和概率

☉江苏省泗洪中学 孙艳艳

2012年高考数学对概率部分主要考查了古典概型、几何概型，考查了相互独立事件的概率乘法公式、互斥事件的概率加法公式以及离散型随机变量的概率分布，考查了数学期望和方差的求法．单纯对排列组合的考查一般在客观题中出现，解答题中对排列组合的考查往往以概率题为载体.排列、组合和概率题整体平稳，难度较往年有所降低.

一、方法技巧

1.解排列应用题的主要方法：若没有限制条件一般用直接法，若存在限制条件的问题，根据不同的题型可采用间接法.具体如下：①每个元素都有附加条件的采用列表法或树状图法；②有特殊元素或特殊位置的要对特殊元素和特殊位置优先考虑；③相邻问题用捆绑法；④不相邻问题用插空法.

2.组合问题常有以下题型：①“有”或“没有”某些元素的组合问题：“有”某些元素的话，则先将这些元素取出，再由另外元素补足；“没有”某些元素的话，则先将这些元素剔除，再从剩下的元素中选取.②“至少”或“至多”或“最多”含有几个元素的题型：解决这类题必须十分重视“至少”、“至多””、“最多”这些关键词的含义，谨防重复与漏解.对于这类问题用直接法和间接法都可以求解，但是如果用直接法分类复杂时，考虑逆向思维，用间接法处理.

3.古典概型的计算方法，要分清基本事件总数n与事件A包含的基本事件数m.

4．几何概型求解的概率问题和古典概型的思路是相同的，同属于“比例解法”．随机事件A的概率可以用“事件A包含的基本事件所占的图形的长度、面积、体积等”与“试验的基本事件所占的总长度、总面积、总体积等之比来表示”.

5.互斥事件有一个发生的概率：P（A＋B）＝P（A）＋P（B）.特例：对立事件的概率：P（A）＋P（B）＝P（A＋B）＝1.

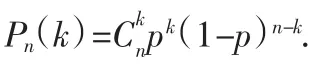
二、高考真题——排列、组合问题

例1 （2012年高考新课标理2）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（ ）.

A.12种 B.10种 C.9种 D.8种

解析：先安排老师有A12=2种方法，再安排学生有C24=6种方法，所以共有12种安排方案，选A.

点评：这是一道排列、组合相结合的题目，准确把握题意是解题的关键.

例2 （2012年高考浙江理6）若从1，2，3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有（ ）.

A.60种 B.63种 C.65种 D.66种

解析：从1，2，3，…，9这9个整数中同时取4个不同的数，其和为偶数的取法分为三类；第一类是取4个偶数，即C45=5种方法；第二类是取2个奇数，2个偶数，即C2C2=60种方法；第三类是取4个

54奇数，即C44=1种方法.故有5+60+1=66种方法.故选D.

点评：两个计数原理是解决排列组合问题最基本的依据，所以我们先分类，每一类中用了组合的知识.本题需要注意的是只取不排.

例3 （2012年高考辽宁理5）一排9个座位坐了3个三口之家，若每家人坐在一起，则不同的坐法种数为（ ）.

A.3×3！B.3×（3！）3C.（3！）4D.9！

解析：此排列可分两步进行，先把三个家庭分别排列，每个家庭有3!种排法，三个家庭共有3!×3!×3!=（3!）3种排法；再把三个家庭进行全排列，有3!种排法.因此不同的坐法种数为（3!）4，答案为C.

点评：本题主要考查分步计数原理，考查分析问题、解决问题的能力，属于中档题.

三、高考真题——概率问题

例4（2012年高考辽宁理10）在长为12cm的线段AB上任取一点C.现作一矩形，领边长分别等于线段AC、CB的长，则该矩形面积小于32cm2的概率为（ ）.

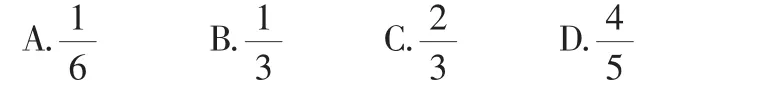
解析：设线段AC的长为xcm，则线段CB的长为（12－x）cm，那么矩形的面积为x（12－x）cm2，

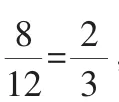
点评：本题主要考查函数模型的应用、不等式的解法、几何概型的计算，以及分析问题的能力.属于中档题.

图1

点评：本题目是概率与线性规划、平面几何的整合的几何概型问题.很明显概率的求法需要用到两个图形的面积之比.

例6（2012年高考湖南理17）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如表1所示.

一次购物17件及以上顾客数（人） x 30 25 y 10量 1至4件 5至8件 9至12件 13至16件结算时间（分钟/人） 1 1.5 2 2.5 3

已知这100位顾客中的一次购物量超过8件的顾客占55%.

（1）确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望.

（2）若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率.（注：将频率视为概率）

解析：（1）由已知，得25+y+10=55，x+y=35，所以x=15，y=20.

该超市所有顾客一次购物的结算时间组成一个总体，所以收集的100位顾客一次购物的结算时间可视为总体的一个容量随机样本，将频率视为概率得：

（2）记A为事件“该顾客结算前的等候时间不超过2.5分钟”，Xi（i=1，2）为该顾客前面第i位顾客的结算时间，则P（A）=P（X1=1且X2=1）+P（X1=1且X2=1.5）+P（X1=1.5且X2=1）.

由于顾客的结算相互独立，且X1，X2的分布列都与X的分布列相同，

点评：本题考查概率统计的基础知识，考查分布列及数学期望的计算，考查运算能力、分析问题的能力.第（1）问中根据统计表和100位顾客中的一次购物量超过8件的顾客占55%知25+y+10=100×55%，x+y=35，从而解得x，y，计算每一个变量对应的概率，从而求得分布列和期望；第（2）问，通过设事件，判断事件之间的互斥关系，从而求得该顾客结算前的等候时间不超过2.5分钟的概率.

预测2013年高考，排列、组合及排列、组合与概率的综合应用问题仍是高考的重点，至少出现一道解答题，重点考查学生的运算能力与逻辑推理能力．猜想在2013年的高考题中客观题仍然可能考查单纯排列、组合问题，而概率问题将放在解答题中考查，试题难度不大，但背景比较新颖.理科出现随机变量，难度比文科大.命题方向以分类思想为主.对古典概型求概率、独立重复试验、事件的相互独立性考查的几率大大增加，所以复习时要有针对性.